Two Ways of Sharing in Division—Let's Practice!
- Understanding Two Ways of Sharing in Division – Introduction
- What Are Two Ways of Sharing in Division?
- Solving Division Problems Using Two Ways of Sharing – Example
- Understanding Two Ways of Sharing in Division – Guided Practice
- Using Two Ways of Sharing in Division – Application
- Solving Division Problems Using Two Ways of Sharing – Summary
- Solving Division Problems Using Two Ways of Sharing – Frequently Asked Questions


Basics on the topic Two Ways of Sharing in Division—Let's Practice!
Understanding Two Ways of Sharing in Division – Introduction
We're diving into the world of division by exploring two ways to share numbers. This method helps us understand how numbers can be divided into equal groups. Get ready because, we're going to practice this together!
What Are Two Ways of Sharing in Division?
Two ways of sharing in division involve creating equal groups from a number. This method helps us see the different ways a number can be divided evenly.
Here are the steps to tackle division using two ways of sharing:
| Step # | Action |
|---|---|
| 1 | Identify the total number to be divided. |
| 2 | Find one way to share the number into equal groups. |
| 3 | Find another way to share the number into equal groups. |
| 4 | Verify that both ways share the number equally. |
| 5 | Check your answer to ensure it makes sense with the problem. |
Let's practice understanding this method with a few examples.
Solving Division Problems Using Two Ways of Sharing – Example
Example 1:
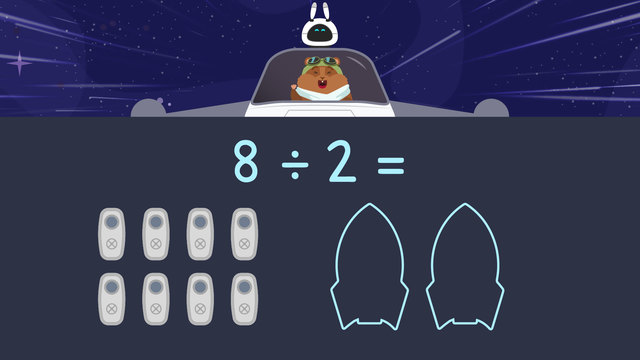
Problem: What are two ways to share eight?
Steps to Solve the Problem:
| Step # | Action | Solution |
|---|---|---|
| 1 | Identify the total number. | 8 |
| 2 | Share eight into two groups. | 2 groups of 4 |
| 3 | Share eight into four groups. | 4 groups of 2 |
| 4 | Verify both ways. | Both are correct. |
Solution: We can make 2 groups of 4 and 4 groups of 2.

Example 2:
Problem: What are two ways to share ten?
Steps to Solve the Problem:
| Step # | Action | Solution |
|---|---|---|
| 1 | Identify the total number. | 10 |
| 2 | Share ten into five groups. | 5 groups of 2 |
| 3 | Share ten into two groups. | 2 groups of 5 |
| 4 | Verify both ways. | Both are correct. |
Solution: We can make 5 groups of 2 and 2 groups of 5.
Understanding Two Ways of Sharing in Division – Guided Practice
Take a look at these numbers: What are two ways to share fourteen?
In number sentence form: 14 ÷ 2 = 7 and 14 ÷ 7 = 2
Using Two Ways of Sharing in Division – Application
Now it's your turn. Solve these problems on your own.
What are two ways to share twenty-two?
In number sentence form: 22 ÷ 2 = 11 and 22 ÷ 11 = 2
Solving Division Problems Using Two Ways of Sharing – Summary
Key Learnings from this Text:
- Solving division problems using two ways of sharing can be achieved by following these steps:
| Step # | Action |
|---|---|
| 1 | Identify the total number to be divided. |
| 2 | Find one way to share the number into equal groups. |
| 3 | Find another way to share the number into equal groups. |
| 4 | Verify that both ways share the number equally. |
| 5 | Check your answer to ensure it makes sense with the problem. |
- Mastering the use of two ways of sharing in division is an important foundational math skill.
Keep practicing these steps, and you'll become a pro at solving division problems using two ways of sharing! Check out more fun math challenges and exercises on our website to continue sharpening your skills.
Solving Division Problems Using Two Ways of Sharing – Frequently Asked Questions
Transcript Two Ways of Sharing in Division—Let's Practice!
Razzi says get these items ready (...) Because today we're going to practice... Two Ways of Sharing in Division. It's time to begin! What are two ways to share eight? Pause the video to work on the problem (...) and press play when you are ready to see the solution! We can make (...) TWO groups of FOUR. And (...) FOUR groups of TWO. Did you also get this answer? Let's tackle the next problem! What are two ways to share ten? Pause the video to work on the problem (...) and press play when you are ready to see the solution! We can make (...) FIVE groups of TWO. And (...) TWO groups of FIVE. Did you also get this answer? Let's try another! What are two ways to share fourteen? Pause the video to work on the problem (...) and press play when you are ready to see the solution! We can make (...) SEVEN groups of TWO. And (...) TWO groups of SEVEN. Did you also get this answer? Let's try one more! What are two ways to share twenty-two? Pause the video to work on the problem (...) and press play when you are ready to see the solution! We can make (...) TWO groups of ELEVEN. And (...) ELEVEN groups of TWO. Did you also get this answer? Razzi had so much fun practicing with you today! See you next time!
Two Ways of Sharing in Division—Let's Practice! exercise
-
Can you find another way of sharing these groups?
HintsUse the arrays to help you.
- The rows represent the groups.
- The columns show how many are in each group.
Here we can see one column circled.
Remember, we use the same numbers both times.
For example, if 18 can be divided into 2 groups of 9, it can also be divided into 9 groups of 2.
Solution15
- 3 groups of 5
- 5 groups of 3
21
- 7 groups of 3
- 3 groups of 7
-
How can we share these numbers?
HintsHow many rows are there in the array? This represents the number of groups.
How many spots in each row? This represents the number in a group.
For example, here 8 has been divided into 4 groups of 2. It could also be divided into 2 groups of 4.
SolutionHere we can see two ways of sharing 6:
- 2 groups of 3
- 3 groups of 2
10
- 2 groups of 5
- 5 groups of 2
20
- 5 groups of 4
- 4 groups of 5
24
- 6 groups of 4
- 4 groups of 6
-
What are the two ways these numbers have been shared?
HintsHow can the numbers 16 and 18 be shared? What are the factors of 16 and 18? Are there factors that match the arrays?
Look at the number of rows. This represents the number of groups. This pictures shows there are two rows altogether.
How many spots in a row? This represents the number in a group. This pictures shows eight spots in one row.
Solution16
- 2 groups of 8
- 8 groups of 2
18
- 3 groups of 6
- 6 groups of 3
-
What is the number?
HintsLook at the number of rows and columns. Can you think of a number that has these factors?
Multiply the number of rows by the number of columns.
For example, these arrays show:
- 2 groups of 5
- 5 groups of 2
Count all of the dots in an array to check.
SolutionThese two arrays showed two ways of sharing 8.
- 2 groups of 4 = 8
- 4 groups of 2 = 8
Two ways of sharing 27
- 3 groups of 9
- 9 groups of 3
Two ways of sharing 18
- 2 groups of 9
- 9 groups of 2
Two ways of sharing 12
- 2 groups of 6
- 6 groups of 2
-
What are two ways of sharing 12?
HintsHow many rows of dots are there? This shows the number of groups.
How many dots in a row? This represents the number in a group.
For example, this array shows 2 groups of 4.
SolutionTwo ways that 12 can be shared are:
- 4 groups of 3
- 3 groups of 4
-
Can you find all of the ways of sharing these numbers?
HintsList all of the factors of each number. Which ones can we multiply together to make the number?
Draw some arrays to help you.
For example, this array has 10 groups of 3. It will help you fill in some answers above.
Solution24
- 1 group of 24
- 2 groups of 12
- 3 groups of 8
- 4 groups of 6
- 6 groups of 4
- 8 groups of 3
- 12 groups of 2
- 24 groups of 1
30
- 1 group of 30
- 2 groups of 15
- 3 groups of 10
- 5 groups of 6
- 6 groups of 5
- 10 groups of 3
- 15 groups of 2
- 30 groups of 1