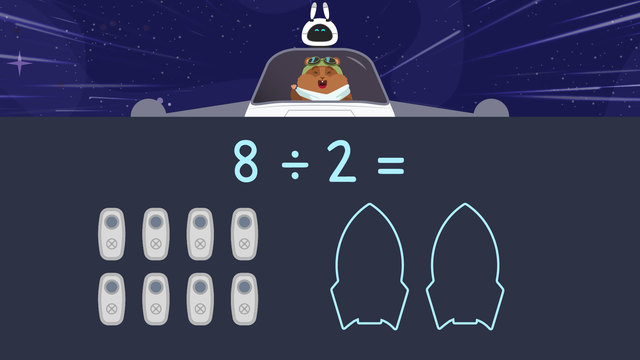
Two Ways of Sharing in Division


Basics on the topic Two Ways of Sharing in Division
Division by Grouping
Division by grouping is a little different from division by sharing. Division by sharing is when we know the number being divided and the number of groups, and we need to find out the number in each group. The division by grouping method happens when we know how many we need to divide into groups, and we need to find out the number of groups. Division sharing and grouping are different as you can see.
Division by Grouping – Example
How do you divide by grouping? The next section explains how to do division as grouping. The image below shows how to solve by dividing in groups. You can see that there are six circles and we need to divide by equal grouping.
There are two ways we can divide six. One way we can divide six is into two groups of three. Another way we can divide six is three groups of two.
Division by Grouping – Worksheets
The table below shows how the method of division by grouping differs from division by sharing.
| Method | What to do |
|---|---|
| division by grouping | It is known how many we need to divide into groups, and we need to find out the number of groups. |
| division by sharing | The number being divided and the number of groups is known, and we need to find out the number in each group. |
Have you practiced yet? On this website you can practice division by grouping and find division by grouping worksheets along with other activities, and exercises.
Transcript Two Ways of Sharing in Division
Mr. Squeaks and Imani are in Egypt and decide to explore a pyramid. It looks like a division problem! Maybe if they solve it the door will open so they can explore further! Let's help Mr. Squeaks and Imani by calculating, "Two Ways of Sharing in Division". When we divide, we break a number up into an equal number of parts, or groups. We will be practicing TWO DIFFERENT WAYS to share numbers into equal groups. First on the wall, there are six circles. One way we can share six into equal groups is to make (...) TWO groups of THREE. What is another way to share six into equal groups? (...) We can also make (...) THREE groups of TWO. What do you notice about the two different ways to share? (...) They are factor pairs of six! Remember, factor pairs are two numbers that are multiplied together to make a product, (...) or in this case the number six! When we calculate different ways to share into equal groups, we can use the factor pairs to help us! Wow! (...) Look at all the jars on the other side... but how do we get over there? If we calculate two ways to share fifteen, a bridge might appear! What is one way to share fifteen into equal groups? (...) We can make (...) THREE groups of FIVE. Thinking about the factor pairs, what is another way to share FIFTEEN into equal groups? (...) We can make (...) FIVE groups of THREE. Since we calculated two ways to share fifteen the bridge has appeared! Now, Mr. Squeaks and Imani are at another door. Let's help them calculate two ways to share twenty-one and maybe we'll see what's inside! This time try to find both ways on your own! Pause the video so you have time to work (...) and press play again when you're ready to see the answer! First, we can make (...) THREE groups of SEVEN... and SEVEN groups of THREE! (...) We found both ways to share twenty-one! It worked (...) but before we see what's inside the door, let's summarize. Remember (...) when we divide, we break a number up into an equal number of parts, or groups. We can identify different ways to share numbers into equal groups using factor pairs. Let's check in with Mr. Squeaks and Imani to see what's behind the door. Oh! What do we have here?! It looks like this mummy is excited to them!
Two Ways of Sharing in Division exercise
-
Which number is being shared?
HintsWhat is the total number of counters in each array?
For example, this array is made of two rows of two so the number being shared is 4.
SolutionThe number being shared here is 15.
It has been shared into:
- Five rows of three
- Three rows of five
The other numbers being shared are:
6
- Two rows of three
- Three rows of two
- Two rows of four
- Four rows of two
- Three rows of four
- Four rows of three
-
Match the two ways of sharing.
HintsWhich number is being represented by the array? Can you find a matching partner?
For example, both of these arrays represent eight.
Four rows of two equals eight and two rows of four equals eight.
SolutionHere we can see the matching arrays.
10
- Two rows of five
- Five rows of two
- Two rows of seven
- Seven rows of two
- Three rows of six
- Six rows of three
- Four rows of five
- Five rows of four
-
Highlight two ways of sharing.
HintsFind the total of each array and then find another one with the same total.
For example, here we have two ways of sharing 20.
SolutionHere are the two ways of sharing each number.
21
- Three rows of seven
- Seven rows of three
- We can see these in green
- Four rows of six
- Six rows of four
- We can see these in yellow
- Three rows of nine
- Nine rows of three
- We can see these in blue
- Five rows of six
- Six rows of five
- We can see these in violet
-
Can you fill in the gaps?
HintsLook at the first way of sharing and think about what a second way could be.
For example, here we can see four ways of sharing twelve.
You could draw an array to help you find the other ways of sharing.
SolutionHere we have four ways of sharing each number.
_______________________________________________________
24
- Three times eight and eight times three
- Four times six and six times four
- Four times eight and eight times four
- Sixteen times two and two times sixteen
- Four times ten and ten times four
- Five times eight and eight times five
- Six times eight and eight times six
- Four times twelve and twelve times four
-
Can you find the other way to share twelve?
HintsWhich array represents twelve?
If we know two rows of six equals twelve how could we flip this to find another way of sharing twelve?
SolutionThe correct answer is six rows of two. This also equals twelve.
-
How many ways can these numbers be shared?
HintsThink about all of the factors of these numbers.
For example, twelve has six ways of sharing:
- 1 x 12
- 2 x 6
- 3 x 4
- 4 x 3
- 6 x 2
- 12 x 1
Draw arrays to help you figure out how many ways you could share each number.
SolutionThe grid shows you how many ways we could share each of these numbers.
Each way of sharing can be drawn as an array. For example 8 can be shared four ways.
- One row of eight
- Two rows of four
- Four rows of two
- Eight rows of one
8
- 1 x 8
- 2 x 4
- 4 x 2
- 8 x 1
- 1 x 16
- 2 x 8
- 4 x 4
- 8 x 2
- 16 x 1
- 1 x 20
- 2 x 10
- 4 x 5
- 5 x 4
- 10 x 2
- 20 x 1
- 1 x 24
- 2 x 12
- 3 x 8
- 4 x 6
- 6 x 4
- 8 x 3
- 12 x 2
- 24 x 1