Comparison Shopping: Unit Price and Related Measurements

Basics on the topic Comparison Shopping: Unit Price and Related Measurements
After this lesson, you will be able to use unit price to make comparisons in tables, equations, graphs, and real-world scenarios.
The lesson begins with how to determine unit rate, using tables, graphs, and equations. This leads to a strategy for comparing unit rates, to determine the best value. The video concludes with a scenario that uses unit price to make comparisons.
Learn about unit price by helping Gabe get the best value when upgrading his Galactic Gorillas action figures!
This video includes key concepts, notation, and vocabulary such as: unit rate (the ratio of two measurements in which the second term is 1); unit price (a unit rate which measures cost per item); the graph of a direct proportion (a line that goes through the origin); slope (the rate of change in a linear equation).
Before watching this video, you should already be familiar with unit rates and setting up and solving proportions.
After watching this video, you will be prepared to use rates to convert from one measurement unit to another.
Common Core Standard(s) in focus: 6.RP.2, 6.RP.3.b A video intended for math students in the 6th grade Recommended for students who are 11-12 years old
Transcript Comparison Shopping: Unit Price and Related Measurements
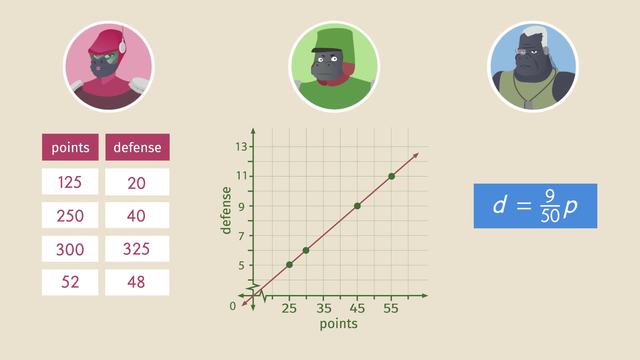
Gabe is always playing his Galactic Gorillas toys-to-life video game, which allows him to bring special action figures to life. Gabe is currently deciding which character's defense to upgrade using the points he has earned from hours of play. To figure out how to get the best value per point, let's see how Gabe applies comparison shopping using unit price and related measurements. This table shows how many points Gabe has to spend in order to upgrade his defense units for Corporal Greta. This graph shows the same relationship for Private Gary. And this equation shows Major George's defense units based on points spent. Which character will give Gabe the best defense per point? To find out, let's determine the unit rate of each offer. Remember, UNIT RATE is the ratio of two measurements in which the second term is 1. The table, graph, and equation each express the value of Gabe's points for defense in different ways. To compare all three, we convert each of the representations to the same rate: defense to points. To find the unit rate per point in the table, pick any row. This row tells us that for 250 points we can get 40 defense units. Putting these values into our ratio, we can now divide 40 by 250. This gives us a unit rate of zero point one six defense units per point. Now looking at the graph for Private Gary, we notice that this line goes through the origin. This means the graph represents a direct proportion. Therefore, to find the unit rate we can pick any point and put it into our ratio of defense to points. Let's pick this point, 55, 11. 11 over 55 simplifies to one fifth. In order to compare we need to find the unit rate per point. So, we still need a one in the denominator. To get that, we divide 5 by 5. And to keep the ratio equivalent, we must also divide 1 by 5. That gives us the unit rate of zero point 2 defense units per point. When looking at this linear equation for Major George, can you identify the slope? If you said 9 over 50, you're right! To make sure this slope actually represents the defense over points rate, we could isolate the ratio by dividing both sides by p. This gives us the proportion d over p equals 9 over 50, where 'd' represents defense and 'p' stands for points. So, 9 to 50 is the defense to points rate. However, we still need the unit rate per point. Just like before, we divide the numerator and denominator both by the value in the denominator, and are now left with zero point one eight defense units per point. Comparing the three unit rates, we see that Gabe's points get him the most defense with Private Gary. Time to upgrade, but whoa! Wait! What's that? An online deal for a four pack of the newest toys to life figurines in the Galactic Gorillas collection? "And it only costs $34.40 with free shipping!" Gabe is lacking these four action figures and has gotta collect 'em all. However, Gabe seems to remember a recent advertisement for a Galactic Gorillas sale at his local shop. At the shop, individual packs of the four action figures now cost $9 a piece. The two-packs costs $17 and come in all the possible combinations. If he wants the best deal, should he buy four individual packs, two two-packs, or the four-pack? To find out, let's determine the unit rate of each offer. In this situation the unit rate tells us how much a single figurine costs, no matter the packaging. So we can call it unit price, because we are looking at the cost per unit. When we compare unit prices, we can easily see which deal is the best buy. We already know the unit price for the single-pack is $9. We can see the ratio of cost per unit holds true at $9 per figurine. The two-pack costs $17 for two figurines. Therefore, we can substitue into the ratio 17 dollars to two figurines and just divide. This means the unit price is $8.50 per figurine in the two-pack. The four-pack costs $34.40. To get the unit price we set-up the ratio again. This allows us to take 34.40 and divide it by 4. That gives us the unit rate of $8.60 per figurine. Now we can compare the unit prices for the various packages. This shows us that $8.50 is the lowest unit price, and therefore the best deal. Because Gabe still wants all four figurines, he decides to buy two of the two-packs to complete his Galactic Gorillas collection. Let's summarize the steps he took to be a comparison shopping pro. We compared unit rates, sometimes known as unit prices. Unit rates can be located in tables, graphs, equations, and real-life scenarios. To find the unit rate in any of these situations, first, set-up the ratio for the rate you want to find. Second, substitute your corresponding values. Third, reduce to a denominator of one by dividing. Looks like Gabe will be able to always find the best bargain in order to save. But something else catches his attention. No wonder they were having a sale. Looks like Galactic Gorillas was so last week.
Comparison Shopping: Unit Price and Related Measurements exercise
-
Find the rate and unit rate from multiple representations.
HintsTo find a unit rate from a table or graph, set up the ratio for the unit rate using information given in either the table or graph.
To find a unit rate from an equation, use opposite operations to bring both variables to one side. For example in $y=\frac{2}{5}x$, bring the $x$ to the left side by dividing both sides by $x$ to get $\frac{y}{x}=\frac{2}{5}$.
The unit rate is the ratio of two measurements in which the second term is $1$.
Solution- To find the unit rate from a table, pick any row except for the one that contains $(0,0)$. ($(0,0)$ is the origin, which is a part of every proportional relationship, so it will not help us to find the unit rate for any specific relationship.) Put the values in the ratio $\frac{\text{Distance}}{\text{Time}}$. Simplify the fraction to get a unit rate.
- To find the unit rate from a graph, first check to see if the graph goes through the origin. This graph does, so the graph represents a direct proportion. To start, pick any point on the line, other than $(0,0)$. Then put the values into the ratio $\frac{\text{Distance}}{\text{Time}}$. Simplify the fraction to get the unit rate.
- To find the unit rate from an equation, isolate the ratio by dividing both sides by $t$. This gives us the proportion $\frac{d}{t}=$unit rate. Simplify the fraction to get a unit rate.
-
Determine the best price by identifying the unit price.
HintsDetermine the unit price for each deal.
Set up the ratio of $\frac{\text{cost}}{\text{unit}}$, then divide to simplify.
For example, let's say a five pack of figurines sold for $\$63.75$. The $\frac{\text{cost}}{\text{unit}}$ ratio would be $\frac{63.75}{5}$. Simplified $\frac{63.75}{5}=12.75$. So the unit price for this example is $\$12.75$.
SolutionThe order from least to most expensive is:
$1)$ A four pack of Cat Hero figurines for $\$41.50$.
- First, set up the $\frac{\text{cost}}{\text{unit}}$ ratio: $\frac{41.50}{4}$.
- Then, divide $\frac{41.50}{4}=10.35$.
- So, the unit price for this deal is $\$10.35$.
- First, set up the $\frac{\text{cost}}{\text{unit}}$ ratio: $\frac{11.50}{1}$.
- Then, divide $\frac{11.50}{1}=11.50$.
- So, the unit price for this deal is $\$11.50$.
- First, set up the $\frac{\text{cost}}{\text{unit}}$ ratio: $\frac{24.00}{2}$.
- Then, divide $\frac{24.00}{2}=12.00$.
- So, the unit price for this deal is $\$12.00$.
- First, set up the $\frac{\text{cost}}{\text{unit}}$ ratio: $\frac{36.75}{3}$.
- Then, divide $\frac{36.75}{3}=12.25$.
- So, the unit price for this deal is $\$12.25$.
-
Find the unit rate.
HintsConvert each representation to the same rate: cost to quantity.
$\frac{\text{cost}}{\text{quantity}}=\frac{y}{x}$.
Once you have the ratio of $\frac{\text{cost}}{\text{quantity}}$, we want to have a denominator of one. Simplify by dividing both the numerator and denominator by the value in the denominator.
SolutionTo be successful in this problem, you need to set up a ratio of cost to quantity for each representation. It is important to note that the directions labeled $x$ as quantity and $y$ as cost. Therefore, $\frac{\text{cost}}{\text{quantity}}=\frac{y}{x}$.
$~$
To determine the unit rate from a table, choose any point, set up the ratio, then divide to simplify.
- Grapefruit: Let's choose the first point, $(4,6)$, substitute into the ratio $\frac{6}{4}$, then simplify by dividing $\frac{6}{4}=1.5$. Therefore, the unit rate for grapefruit is $1.5$.
- Apples: Let's choose the first point, $(10,4)$, substitute into the ratio $\frac{4}{10}$, then simplify by dividing $\frac{4}{10}=0.4$. Therefore, the unit rate for grapefruit is $0.4$.
To determine the unit rate from a graph, choose any point on the line, other than $(0,0)$, set up the ratio, then divide to simplify. $~$
- Watermelon: Let's choose the point $(1,4)$. Substitute this point into the ratio $\frac{4}{1}$, then simplify by dividing $\frac{4}{1}=4$. Therefore, the unit rate for watermelon is $4$.
- Mangos: Let's choose the point $(2,5)$. Substitute this point into the ratio $\frac{5}{2}$, then simplify by dividing $\frac{5}{2}=2.5$. Therefore, the unit rate for mangos is $2.5$.
To find the unit rate from an equation, isolate the ratio by multiplying both sides by $x$.
- Strawberries: First, isolate the ratio to get $\frac{y}{x}=\frac{1}{4}$. Now, simplify $\frac{1}{4}$ by dividing to get $\frac{1}{4}=0.25$. Therefore, the unit rate for strawberries is $0.25$.
-
Identify the steps used to determine a unit rate.
HintsIdentify the ratio.
Use the numbers given in the example to substitute into the ratio.
Recall that a unit rate is a ratio of two measurements in which the second term is $1$.
SolutionThere are three basic steps to follow when comparison shopping:
- Set up the ratio.
- Substitute in values.
- Reduce to the unit rate.
- Set up the ratio.
- $\frac{\text{cost}}{\text{unit}}$
- Substitute in values.
- Deal A: $\frac{28.50}{3}$ and Deal B: $\frac{46.25}{5}$
- Reduce to the unit rate by dividing.
- Deal A: $\frac{28.50}{3}=9.50$ and Deal B: $\frac{46.25}{5}=9.25$
- The unit rate for Deal A is $\$9.50$ and the unit rate for Deal B is $\$9.25$. Therefore, Deal B has a smaller price per unit.
-
Define rate and unit rate.
HintsSome examples of rates are: $7$ apples to $6$ oranges, $4$ cups of flour per $2$ cups of milk, and $70$ miles per $2$ hours.
Some examples of unit rates are: defense per point, cost per unit, and miles per hour. Point, unit, and hour are singular.
When simplifying a unit rate, the goal is to make the denominator $1$.
SolutionThe definition of unit rate is the ratio of two measurements in which the second term is $1$.
The definition of rate is a ratio that compares two different quantities.
Unit rate and rate are similar because they both compare two measurements, but in a unit rate the second measurement is always reduced to $1$.
-
Determine the best deal using unit rate.
HintsSet up the $\frac{\text{cost}}{\text{unit}}$ ratio and simplify.
Make a list of the possible combinations of packs Gabe's sister can buy that will give her a total of five figurines. For example $2+3=5$, what are some other combinations? Think outside of the box, she doesn't only have to buy two packs.
Substitute in the cost for each for each pack to determine which combination is the cheapest. For example a two-pack and a three-pack will give her five figurines. The cost of a two-pack is $\$9.50$ and the cost of a three pack is $\$13.50$, so the total cost would be $\$23.00$.
SolutionTo answer this problem, first find the cost per unit for each pack of figurines.
- One figurine for $\$5.00$, so $\frac{5.00}{1}=5.00$
- Two figurines for $\$9.50$, so $\frac{9.50}{2}=4.75$
- Three figurines for $\$13.50$, so $\frac{13.50}{3}=4.50$
- Four figurines for $\$17.00$, so $\frac{17.00}{4}=4.25$
The cheapest cost per unit is $\$4.25$ from the four-pack.
$~$
Second, think of all possible combinations of packs that will result in five figurines.
- $2+3=5$
- $1+4=5$
- $2+2+1=5$
- $3+1+1=5$
- $2+1+1+1=5$
- $1+1+1+1+1=5$
Now, substitute in each cost per pack to determine the cheapest option for five figurines.
- $2+3=5\\ 9.50+13.50=23.00$
- $1+4=5\\5.00+17.00=22.00$
- $2+2+1=5\\ 9.50+9.50+5=24.00$
- $3+1+1=5\\ 13.50+5+5=23.50$
- $2+1+1+1=5\\ 9.50+5.00+5.00+5.00=24.50$
- $1+1+1+1+1=5\\ 5.00+5.00+5.00+5.00+5.00=25.00$
The cheapest total is $\$22.00$ from the combination of $1+4$, so Gabe's sister should buy $1$ one-pack and $1$ four-pack.

From Ratios to Rates and Rates to Ratios

Finding Rates with Division

Comparison Shopping: Unit Price and Related Measurements

Getting the Job Done—Speed

Getting the Job Done—Work
Getting the Job Done: Converting Units of Measurement

Problem Solving Using Rates, Unit Rates, and Conversions

What is a Proportional Relationship?











