Getting the Job Done: Converting Units of Measurement

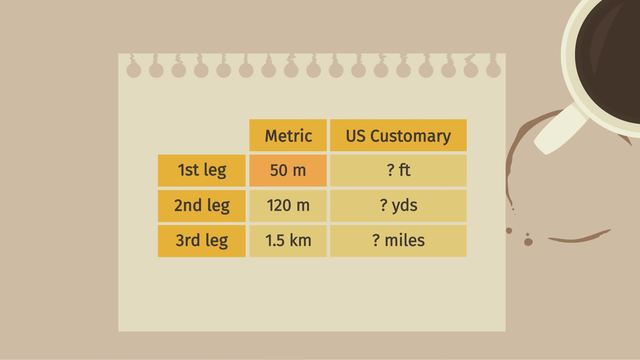
Maxwell is an engineer at NASA, programming the driving distances for the Mars Rover. Suddenly he gets a call from the EUROPEAN Space Agency! Their Mars orbiter has detected some signals near the Rover that might indicate life on Mars! Maxwell quickly records the driving distances he’ll need to program for the Rover. Hopefully he can program the Rover better than he programmed this pesky robotic arm! The Europeans want the Rover to visit three spots, so they gave Maxwell three distances for the Rover to drive.

But the distances are in meters and kilometers, which are metric units. Since the Rover doesn't understand metric units, Maxwell will need to convert them to feet, yards, and miles, which are the units of the US Customary system. He needs to get the job done by converting units of measurement to make sure the Rover gets there before the signs of life disappear. The Rover first needs to drive 50 meters. We need to convert the 50 meters to feet so the Rover can get moving. The ratio of a measurement in one unit to the same measurement in a second unit is always the same. In this case, the ratio of meters to feet will be a constant, so using equivalent ratios can help us solve this problem. Remember that a ratio table is a table of equivalent ratios, so let's build one. First, Maxwell looks at his conversion table and sees that 1 meter is approximately 3.28 feet. Let's put this info in our ratio table. Then let's put in our known value for the measurement, 50 meters. And then let the variable 'd' represent the distance, in feet. Using our knowledge of proportions, we can then set up the equivalent ratios. That is 3.28 feet over 1 meter is equal to 'd' over 50 meters. To isolate our variable we multipy both sides by 50 meters. Notice that the meters unit cancels out, giving us 'd' is approximately 164 feet. Maxwell got the answer, but is there a quicker way to do it? In the conversion table Maxwell saw that the unit rate is 3.28 feet per one meter. But let's take a look at what a unit rate really means. This means that for every 1 meter, we have about 3.28 feet. That would mean that if we had 2 meters, we would have 2 times 3.28 feet, which is 6.56 feet. And going even further, if we had 50 meters, we would have 50 times 3.28 feet, which is 164 feet. In general, we are multiplying the given measurement by the conversion factor, written as a fraction. Notice that we want our result in feet. Therefore, we've got to eliminate the meters. We can see that the meters unit is in both the numerator and denominator, so it cancels out like any common factor. That leaves us with the desired units, feet. For his next challenge, Maxwell needs to convert 120 meters to another unit the rover can understand, yards. He quickly looks up the conversion factor in a conversion table and sees that 1 meter is equal to about 1.094 yards. Now we need to multiply the given distance by the conversion factor, written as a fraction. If we write it with meters in the numerator, notice that the units don't cancel out. So that's wrong. But if we write meters in the denominator, the units cancel out, leaving us with yards, which is what we wanted! Now we just have to multiply straight across, which gives us that 120 meters is approximately 131.2 yards. Maxwell has one remaining distance to convert, and then he can send the rover on it's way to perhaps find LIFE ON MARS! Maxwell’s final conversion is converting 1.5 kilometers to miles. Maxwell sees in his conversion table that there are approximately 1.609 kilometers in one mile. Like we did before, we will need to multiply our measurement, 1.5 kilometers, by the conversion factor. Since we want the kilometers unit to cancel out, we need to put it in the denominator of our conversion factor. This gives us 1.5 kilometers is approximately equal to 0.93 miles. Maxwell completed all his calculations! Before we send the instructions to the Rover, let's review how to convert units of measurements. First, identify the units you're converting from, and the units you're converting to. Find the unit rate which relates the two units. Write the conversion rate as a fraction, making sure to set up the fraction to eliminate the unwanted units. Then multiply your measurement by the conversion factor, cancelling out the units. After checking his work, Maxwell's ready to contact the Rover and upload the instructions! It's essential that he types the commands correctly. But the robot's arm is acting up again! Oh no! Maxwell loses connection with the Rover. Maxwell! Good luck explaining this one to your bosses at NASA! This shows us that $8.50 is the lowest unit price, and therefore the best deal. Because Gabe still wants all four figurines, he decides to buy two of the two-packs to complete his Galactic Gorillas collection. Let's summarize the steps he took to be a comparison shopping pro. We compared unit rates, sometimes known as unit prices. Unit rates can be located in tables, graphs, equations, and real-life scenarios. To find the unit rate in any of these situations, first, set-up the ratio for the rate you want to find. Second, substitute your corresponding values. Third, reduce to a denominator of one by dividing. Looks like Gabe will be able to always find the best bargain in order to save. But something else catches his attention. No wonder they were having a sale. Looks like Galactic Gorillas was so last week.