Adding and Subtracting Radical Expressions
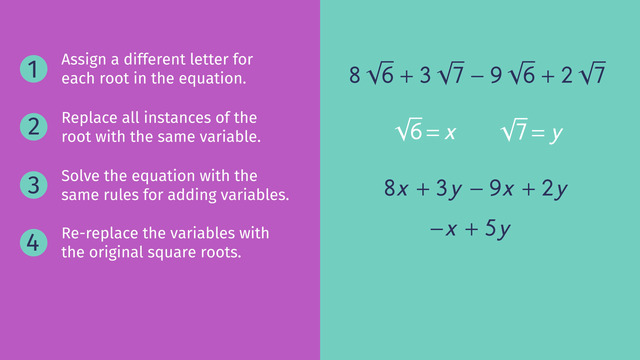

Basics on the topic Adding and Subtracting Radical Expressions
To add or subtract radical expressions, first simplify radicals and then combine like radical terms.
Only like radical terms, or radical expressions which share the same index and radicand, can be added or subtracted. For example, 3√5 + 4√5 = 7√5. In the same manner, 8√3 - 6√3 = 2√3. What about if we’re given with √12 - √48? This becomes √4(3) - √(16)(3) = 2√3 - 4√3 = -2√3.
Radical expressions with different radicands or indices can’t be added or subtracted. Simplifying 9√5 - 2√2 - 3√5 + 5√2 gives us (9√5 - 3√5) + (- 2√2 + 5√2) = 6√5 + 3√2.
Simplifying radical expressions by adding or subtracting radicals is as easy as adding or subtracting like terms in an algebraic expression.
Rewrite expressions involving radicals and rational exponents using the properties of exponents.
CCSS.MATH.CONTENT.HSN.RN.A.2
Transcript Adding and Subtracting Radical Expressions
Meet Clara and her roommate, Maxine. Clara is a very free spirit. This is fine most of the time, but to the chagrin of Maxine, Clara likes to combine everything and Clara cooks for the both of them. Banana and Steak Tacos, Cake and Nacho Cheese, Fish and Chocolate. One day, while sleeping, Maxine slipped some new listening material into Clara’s playlist with one message: stop combining things that shouldn’t be combined. Max doesn’t know how many more blueberry marshmallow pizzas she can eat. The next day, expecting another honey cauliflower salmon dish, Clara’s roommate is pleasantly surprised to be presented with a tasty looking spread. Maxine is ecstatic and curious about what was on the tape.
Adding and Subtracting Radical Expressions
What a weird title for a self-improvement tape. Adding and Subtracting Radical Expressions. Let’s take a listen: Welcome to the relaxation zone, you are fully relaxed. Your eyes are getting heavy. You should combine things like you Add and Subtract Radical Expressions. Radical expressions look daunting, but they’re not. Radical expressions are your friends. Radical expressions are not hard.
Let’s take a closer look. If we have 4 times the square root of 3 plus 5 root 5 plus 6 root 3 minus 2 root 5, we have to first take a look at how many different numbers we have under the radical. In this equation, the numbers under the radical are 3 and 5. First, we have to replace the square root of 3 with ‘x’ and root 5 with ‘y’. Now, we can add the terms together using the rules we already know for adding variables. 4x + 6x = 10x and 5y - 2y = 3y. After we’re sure we’ve simplified things as much as possible, now we can simply plug our roots back in and finish solving the problem.
After substituting the square roots back into the original equation, we get 10 times the square root of 3 plus 3 times the square root of 5. Now, we just have to plug this into our calculator to find the answer: this is about 24.03.
Instruction to add and subtract Radical Expressions
Let’s review the steps again, this time, using different numbers. Step 1: Identify how many different roots there are in the expression and assign each one a letter. Step 2: Replace all instances of the root with the same variable. Step 3: Solve the equation with the same rules for adding variables. Step 4: Re-replace the variables with the original square roots. Step 5: As always, PEMDAS.
Now that we know how to add and subtract radical expressions, let’s get back to the roommates and see what’s cooking. Would ya look at that? Maxine cooked! Clara looks impressed for now.
Adding and Subtracting Radical Expressions exercise
-
Explain how to add and subtract radical expressions.
HintsOnly combine like terms.
You can combine $8x-9x$ as follows: $8x-9x=(8-9)x=-1x=-x$.
Remember to keep track of which letters were assigned to which square roots, so that you can re-replace the variables with the right square roots later.
SolutionThere are two different numbers under square roots, $6$ and $7$, so we want to assign two different letters for each root:
- $\sqrt6=x$
- $\sqrt7=y$
$8x+3y-9x+2y$.
This equation can be solved with the same rules for adding variables:
$8x+3y-9x+2y=8x-9x+3y+2y=-x+5y$.
Lastly re-replace the variables with the original square roots to get the result:
$8\sqrt6+3\sqrt7-9\sqrt6+2\sqrt7=-\sqrt6+5\sqrt7$.
-
Simplify the following expression.
HintsYou can only combine like terms. For instance, we have $3x+3y-2x=3x-2x+3y=x-3y$.
Here is an example of adding two radical expressions together.
$\begin{array}{rcllll} 4\sqrt8+5\sqrt8&=&~?&|& \text{assign } \sqrt8=x\\ 4x+5x&=&~9x&|&\text{re-replace } x=\sqrt8\\ 4\sqrt8+5\sqrt8&=&~9\sqrt8 \end{array}$
SolutionThere are two different numbers under square roots, $3$ and $5$. For these square roots we assign two different letters:
- $\sqrt3=x$
- $\sqrt5=y$
We solve this equation with the same rules for adding or subtracting variables:
$4x+5y+6x-2y=4x+6x+5y-2y=10x+3y$.
Lastly we re-replace the variables with the original square roots to get
$4\sqrt3+5\sqrt5+6\sqrt3-2\sqrt5=10\sqrt3+3\sqrt5$.
-
Decide which terms can be added or subtacted.
HintsWhether or not two radical expressions could be added or subtracted depends only on the numbers under the square roots.
You can only add or subtract radical expressions with same number under the square roots.
For example, you could add or subtract $3\sqrt5$ and $4\sqrt5$, but you can't add or subtract $3\sqrt5$ and $4\sqrt4$.
SolutionKeep in mind that you can only add or subtract radical expressions with the same number under the square roots.
So you can add or subtract the following expressions:
- $3\sqrt6$ and $-\sqrt6$ as well as $7\sqrt6$
- $2\sqrt3$ and $\sqrt3$ as well as $6\sqrt3$
- $\sqrt7$ and $6\sqrt7$ as well as $3\sqrt7$
-
Find the errors in the calculation.
HintsFirst count the different numbers under square roots.
Keep in mind that you only can combine radical expressions with the same number under the square roots.
There are $8$ errors in total.
SolutionHere you see three different numbers under square roots. We assign the variables
- $\sqrt3=x$
- $\sqrt5=y$
- $\sqrt2=z$
$3x+4y-2z+5y-3z+2x$.
We handle this expression by combining like terms:
$3x+4y-2z+5y-3z+2x=3x+2x+4y+5y-2z-3z=5x+9y-5z$.
Lastly we re-replace the variables with the corresponding square roots to get the desired solution:
$3\sqrt3+4\sqrt5-2\sqrt2+5\sqrt5-3\sqrt2+2\sqrt3=5\sqrt3+9\sqrt5-5\sqrt2$.
-
Determine when radical expressions can be added or subtracted.
HintsYou can only combine like terms. For example:
- $3x+4x=7x$
- $3x+4y$ can't be simplified.
You can't simplify an expression like $3\sqrt3+4\sqrt4$.
Remember Maxine's hint on the tape: "Stop combining things that shouldn't be combined.“
SolutionWhat radical expressions can be added or subtracted?
- Could $3\sqrt3$ and $2\sqrt4$ be added or subtracted? No!
- Could $3\sqrt3$ and $2\sqrt3$ be added or subtracted? Yes!
In the first example the numbers under the square roots are different, while in the second both are the same.
You can only add or subtract radical expressions if the numbers under the square roots are the same.
Let's simplify the example above:
- $3\sqrt3+2\sqrt3=5\sqrt3$
- $3\sqrt3-2\sqrt3=\sqrt3$
-
Add or subtract the following radical expressions.
HintsJust follow those steps.
You can only combine radical expressions with the same numbers under the square roots.
SolutionFor adding or subtracting radical expression just follow the following steps:
- Assign a different letter for each root in the equation.
- Replace all instances of the root with the same variable.
- Solve the equation with the same rules for adding variables.
- Re-replace the variables with the original square roots.
$~$
$-3\sqrt5+4\sqrt7+4\sqrt5+3\sqrt7$
- $\sqrt5=x$ and $\sqrt 7=y$
- $-3x+4y+4x+3y$
- $-3x+4y+4x+3y=-3x+4x+4y+3y=x+7y$
- $-3\sqrt5+4\sqrt7+4\sqrt5+3\sqrt7=\sqrt5+7\sqrt7$
$5\sqrt7-4\sqrt5+4\sqrt7+3\sqrt5$
- $\sqrt7=x$ and $\sqrt 5=y$
- $5x-4y+4x+3y$
- $5x-4y+4x+3y=5x+4x-4y+3y=9x-y$
- $5\sqrt7-4\sqrt5+4\sqrt7+3\sqrt5=9\sqrt7-\sqrt5$
$\sqrt7+6\sqrt5+2\sqrt7-2\sqrt5$
- $\sqrt7=x$ and $\sqrt5=y$
- $x+6y+2x-2y$
- $x+6y+2x-2y=x+2x+6y-2y=3x+4y$
- $\sqrt7+6\sqrt5+2\sqrt7-2\sqrt5=3\sqrt7+4\sqrt5$
$7\sqrt7-2\sqrt5+4\sqrt5-3\sqrt7$
- $\sqrt7=x$ and $\sqrt 5=y$
- $7x-2y+4y-3x$
- $7x-2y+4y-3x=7x-3x-2y+4y=4x+2y$
- $7\sqrt7-2\sqrt5+4\sqrt5-3\sqrt7=4\sqrt7+2\sqrt5$