Simplifying Radical Expressions


Basics on the topic Simplifying Radical Expressions
For a radical expression to be in the simplest form, three conditions must be met: 1. The radicand contains no factor greater than 1 that is a perfect square. 2. There is no fraction under the radical sign. 3. There is no radical in the denominator of a fraction. The procedure used to remove a radical from a denominator is called rationalizing the denominator.
A knowledge of perfect squares and the product property of square roots can be very helpful in simplifying radical expressions. The property states that the root of the product of two terms is equal to the product of the root of each term.
To use the product property of square roots to simplify a radical expression, first write the radicand as the product of a perfect square and a factor that does not contain a perfect square. Then use the product property of square roots to write the expression as a product. Finally, simplify the radical expression.
Another useful property for simplifying radical expressions is the quotient property of square roots; it is used to divide radical expressions. The property states that the root of a rational number is equal to the root of the numerator divided by the root of the denominator.
In a similar fashion, the quotient property can be used to simplify a radical expression by first writing the expression as the root of the numerator divided by the root of the denominator, then simplifying the root in the numerator and the root in the denominator, and finally simplifying the resulting radical.
Expressions and Equations Work with radicals and integer exponents.
CCSS.MATH.CONTENT.8.EE.A.2
Transcript Simplifying Radical Expressions
Long, long ago, somewhere in the deep blue of the Caribbean Sea. Two rival pirate captains were madly in love, and as you can imagine, this was quite a complicated situation. To keep their dalliance a secret, they pretended to be mortal enemies, and to prove this, they constantly pretended to try to overpower the other. Captain Bonny hoisted her sails due east while Calico Jack headed south. Bonny had the wind at her back, so she traveled twice as fast as Jack. Only two hours later and with a heavy heart, she wondered how far she was from her paramour’s sloop.
Simplifying radical expressions
Being a math whiz, the lovelorn captain used simplified radical expressions to figure out the distance. Let’s look at her calculations: Bonny travelled a distance equal to 4x, and Jack travelled a distance equal to 2x. Notice the right angle?
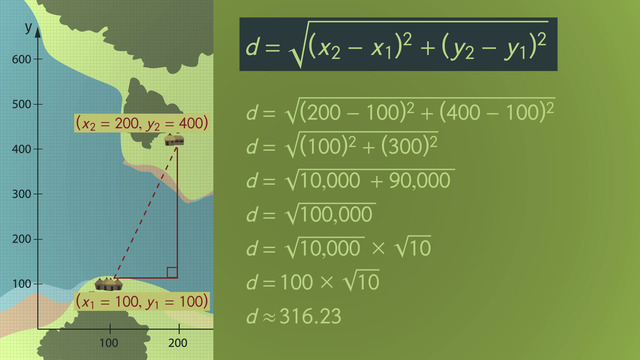
Because the points are in the shape of a right triangle, she used the Pythagorean Theorem to solve for the unknown length. Remember, the Pythagorean Theorem is: a² + b² = c² and 'c' is the hypotenuse, which is the longest side. The hypotenuse is always located opposite the right angle. Now, by subbing in the lengths she knows, Bonny can calculate the unknown length by finding the square root of 20 x².
The notation of roots
Let’s investigate the proper notation for roots. I bet you always wondered about this. The small number is called the index, and it indicates the root. A root of 2 indicates the second root, or the square root; if no number is present, the second root is assumed. The radical is the boxy shape, and the radicand is the number under the box. Understanding and using the correct terms for math can make calculations easier!
Two Properties to solve problems
There are two properties that will help us to solve problems that include square roots. First, let’s review the Product Property of Square Roots:
The square root of the product of 'ab' is equal to the square root of 'a' times the square root of 'b'.
Let’s take a look at an example: what is the square root of 27? First, factor out any perfect squares. In case you forgot, a perfect square is a number that is the square of a rational whole number. Perfect squares are 4, 9, 16, 25, and so on. Back to root 27. Using the Product Property of Square Roots, we can factor out the perfect square of 9. Then, just do the math. The end result is 3 times the square root of 3, or simply, three root three.
The second property is the Quotient Property of Square Roots. The square root of the fraction 'a/b' is equal to the square root of 'a' divided by the square root of 'b'. Let’s sub in some numbers to make this easier to understand. The square root of the fraction 49 over 81 is equal to the square root of 49 over the square root of 81 or 7 over 9.
Back to Captain Bonny. How did she simplify the radical expression of the square root of 20 x²? First, she looked for perfect square factors of 20, oh there’s one: 4! x² is obviously a perfect square, so we can group these two terms together. The rest of the calculations are easier than firing a cannon. The square root of 20x² can be simplified to 2x times the square root of 5.
And speaking of firing a cannon. Is this for real? Oh, so that was her plan all along!
Simplifying Radical Expressions exercise
-
Determine the distance $c$.
HintsYou can use the Pythagorean theorem to determine the missing length.
Don't forget to simplify your answer.
You can simplify your answer using the product property of roots.
SolutionThe distance the ships have traveled and the distance between them form a right angle. We can use the Pythagorean theorem to find the distance between the two ships. The distance between them is the hypotenuse. We have
$a^2 + b^2 = c^2$.
Substituting in known values,
$(2x)^2 + (4x)^2 = c^2$,
and simplifying gives
$4x^2 + 16x^2 = c^2$
$20x^2 = c^2$.
Taking the root of both sides gives
$\sqrt{20x^2} = c$.
Now we have an expression for $c$, and we must simplify it as much as possible. We can do this using the product property of roots:
$c = \sqrt{20x^2}$.
We can start by separating the radicand (the term the root operator is applied to) into a product of two terms, one of which contains only perfect squares:
$c = \sqrt{4x^2 \times 5}$.
We know that the product property of roots states that
$\sqrt{ab} = \sqrt{a} \times \sqrt{b}$.
We can apply this to our solution, to arrive at
$c = \sqrt{4x^2} \times \sqrt{5}$.
We can then simplify this expression to a final answer:
$c = 2x \times \sqrt{5}$.
-
Explain how to multiply and divide radical expressions.
HintsThe name of the property includes either "product" or "quotient", which gives you a hint about what operation it involves.
The properties don't use addition or subtraction.
SolutionThe product property of roots is used to simplify terms that involve multiplication.
The property states that the root of the product of two terms is equal to the product of the root of each term:
$\sqrt{ab} = \sqrt{a} \times \sqrt{b}$.
The quotient property of roots is used to simplify terms that involve division.
The property states that the root of a rational number is equal to the root of the numerator divided by the root of the denominator:
$\sqrt{\dfrac{a}{b}} = \dfrac{\sqrt{a}}{\sqrt{b}}$.
-
Decide which radical expressions can be simplified.
HintsLook for factor pairs of the radicand, where one pair is a perfect square.
Keep in mind that $4$, $9$, $16$, $25$, and $x^2$ are all perfect squares.
SolutionAll of these radical terms involve multiplication, not division. Therefore we should try to simplify each expression using the product property of roots. A radical term can be simplified using this property if its radicand has a factor that is also a perfect square.
Let's look for factors of each radicand, keeping in mind that $4$, $9$, $16$, $25$, and $x^2$ are all perfect squares.
For the first radical term, $\sqrt{32x^2}$, the radicand $32x^2$ has the factor $16x^2$. The square root of this factor is $4x$, so it is a perfect square. Therefore this radical term can be factored. We can prove this by factoring it:
$~$
$\sqrt{32x^2}$
$= \sqrt{16x^2 \times 2}$
$= \sqrt{16x^2} \times \sqrt{2}$
$= 4x \times \sqrt{2}$ ✓
$~$
Similarly, for the other radical expressions...
- $\sqrt{14}$ the radicand $14$ has no factors which are a perfect square. ✗
- $\sqrt{18x}$ the radicand $18x$ has the factor $9$, which is a perfect square. ✓
- $\sqrt{50}$ the radicand $50$ has the factor $25$, which is a perfect square. ✓
-
Determine the missing length.
HintsIt may help to assign a variable to the side length of one of the squares.
You can find the side length of the square using the area of the square, and the fact that the area is equal to the square of the side length.
Don't forget to simplify radical terms.
SolutionJack labels the side length of a square as $s$. He therefore knows that $x = 2s$.
He can also say that the area of the square, $a$, is $a = s^2$.
He knows that the area of the square is $32$ units, so he substitutes this in to get $32 = s^2$.
He applies opposite operations to isolate $s$: $\sqrt{32} = s$.
Now he must simplify the radical to find the value of $s$:
$s = \sqrt{32}$
$s = \sqrt{16 \times 2}$.
Using the product property of roots, he gets
$s = \sqrt{16} \times \sqrt{2}$.
Simplifying gives
$s = 4 \times \sqrt{2}$.
Jack can now find the missing value $x$:
$x = 2s$
$x = 2 \times 4 \times \sqrt{2}$
$x = 8 \sqrt{2}$.
-
Label the parts of a radical expression.
HintsPay close attention to spelling.
The number that indicates what root is being taken is called the index.
SolutionThe small number is called the index. It indicates which root is being taken. It is equal to two in the case of a square root.
The boxy shape that looks a bit like a check mark is called the radical.
The large number, inside the radical, is called the radicand.
-
Simplify the radical expressions.
HintsThe different expressions sometimes share common factors. It may help to start by simplifying each radical expression without looking at the answers.
Each expression can be simplified using the product property of roots.
SolutionEach expression can be simplified using the product property of roots. Let's simplify each radical expression.
For $\sqrt{32}$, $16$ is both a factor of the radicand, and is a perfect square. Let's factor this number out of the radicand: $\sqrt{16 \times 2}$. Now we can used the product property of roots to simplify the radical expression: $\sqrt{16} \times \sqrt{2}$. This simplifies to $4 \times \sqrt{2}$.
Similarly, we can simplify $\sqrt{18}$ into $3 \times \sqrt{2}$.
The radical expression $\sqrt{12}$ becomes $2 \times \sqrt{3}$.
And the expression $\sqrt{48}$ simplifies to $4 \times \sqrt{3}$.
















wooowwww love story yassssss!!!