Multiplying Special Case Polynomials
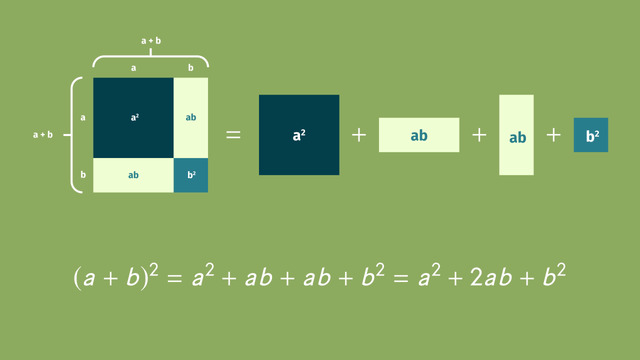

Basics on the topic Multiplying Special Case Polynomials
Are you getting tripped up and slowed down by using the FOIL and area model methods to factor and find the products of polynomials? When working with polynomials, it’s important to keep an eye out for patterns that can help you solve problems quickly and accurately. Watch this video, and you just might learn some new tricks to help you work with special case polynomials.
For the square of a binomial sum, be aware the product is a perfect square trinomial: (a+b)(a+b) = a² + 2ab + b². For the square of a binomial difference, the product is another perfect square trinomial: (a-b)(a-b) = a² -2ab + b². Notice when the terms in the binomials are added, the middle term in the product is positive, and when the terms in the binomials are subtracted, the middle term in the product is negative. The product of a binomial sum and a binomial difference is the difference of two squares or a DOTS: (a+b)(a-b) = a² – b². To identify a DOTS, look for perfect squares.
Watching out for patterns can help you work with polynomials. If you can learn to recognize these three patterns, you can work smart rather than working so darn hard.
Understand the relationship between zeros and factors of polynomials.
CCSS.MATH.CONTENT.HSA.APR.B.2
Transcript Multiplying Special Case Polynomials
GSquared and FoxyCooke are competing hackers. They're always trying to best each other. This time, they're trying to hack into a company’s security system. Whoever gets into the system first will be the winner of eternal fame and glory. GSquared is at the first security wall. To gain access to the first level, he has to simplify this expression, the sum of 'a' and 'b' squared, AKA the sum of 'a' and 'b' times the sum of 'a' and 'b'.
The binomials
GSquared knows a good strategy when he sees one. He uses an area model to find the product of the two binomials.To set up the area model, he divides a rectangle into 2 rows and 2 columns and labels each of the 4 sections with a term from the 2 binomials. Then he calculates the area of each section and writes it down in the corresponding section of the area model.
(a)(a) = a²,
(a)(b) = ab,
(b)(a) = ab,
(b)(b) = b².
Calculate the product of two binomials
He adds the four terms together, groups the like terms and finally, writes the expression in the standard form. The result? a² + 2ab + b². He knows he's got this, so he enters the password…Gosh darn it. That FoxyCooke got here first. GSquared was too slow. Does Foxy know a faster way to calculate the product of two binomials? She does know a faster way…
Simplify the expression
When Foxy saw the expression, she immediately recognized the pattern. She knows the square of a binomial sum is equal to a perfect square trinomial! GSquared reaches the wall of the 2nd level. Hoping to be faster than last time, he tries a different method to simplify the expression. He uses the FOIL method to simplify the difference of a and b times the difference of a and b.
The FOIL method
FOIL stands for first, outside, inside, and last. This is a mnemonic device used to simplify the product of two binomials. Let's try it out, but we have to go fast! First, multiply the first two terms, (a)(a) = a². Next, multiply the outer terms, (a)(-b) = -ab. Now the inside terms, (-b)(a). The product is '-ab'. Last, the last terms, (-b)(-b) = b².
The perfect square trinomial
Combine the like terms and... the simplified expression is a² - 2ab + b². He enters the password and...Although he used the FOIL method, he's foiled again by Foxy – she beat him a second time. How did she do it? Again Foxy recognized a pattern. This expression is the square of a binomial difference and she used another perfect square trinomial to crack the password in just seconds.
Multiplication problem
Finally the last wall... This time the task is a multiplication problem, 42 times 38. GSquared is a pro at multiplication, so he's not worried... Are you kidding me? That Foxy is a real fast fox. Look how she used the difference of two squares to solve the problem fast like lightning. When you have the expression of the sum of a and b times the difference of a and b, watch what happens when you apply the FOIL method the inner and outer products cancel each other out to leave the difference of two squares!
The DOTS expression
This is also known as a DOTS expression That Foxy, she applied DOTS to the number 42 and 38 rewriting them as 40 plus 2 and 40 minus to get a difference of two squares, then she simplified the exponents and calculated the difference to equal 1,596! She recognized the pattern of a difference of two squares!
Pay attention and you'll start to notice these patterned expressions too, just like Foxy. This summary Foxy used is super helpful to help you learn to recognize the polynomial patterns, so you can save time and be Foxy-fast. Foxy's the clear winner, for sure , but hold on... What’s going on here? It looks as though our two hackers got hacked…by their mom! It`s time for dinner.
Multiplying Special Case Polynomials exercise
-
Calculate the term ${(a+b)^2}$.
HintsImagine you cut the square with side lengths ${a+b}$ into two squares and two rectangles.
The area of the original square is the same as the sum of the two smaller squares and two rectangles.
You can also use the FOIL method to simplify ${(a+b)(a+b)}$.
SolutionThe expression ${(a+b)(a+b)}$, or ${ (a + b)^2}$, can be simplified using the area model.
Imagine a square with side lengths ${a+b}$; its area is ${(a+b)^2}$.
You can divide this square into two smaller squares with sides $ a$ and $b$, respectively, as well as two rectangles with a height $a$ and length $b$.
The areas of the squares are ${a^2}$ and ${b^2}$, while each rectangle has an area equal to ${ ab}$.
Combining the like terms gives us ${(a+b)^2=a^2+2ab+b^2}$.
-
Summarize the multiplication of special binomials.
HintsThe difference of two squares is ${(a+b)(a-b)}$.
You can simplify the expansion of binomials by using the FOIL method.
For ${ (a+b)(a+b)}$, use the FOIL method:
F multiply the first ${a \times a}$
O multiply the outer ${a \times b}$
I multiply the inner ${b \times a}$
L multiply the last ${b \times b}$
SolutionHow can you remember the pattern for multiplying of binomials?
Perfect Square Binomials
${ \begin{array}{rcl} (a + b)(a + b) &=&\\ &=& a^2 + ab + ab + b^2\\ &=& a^2 + 2ab + b^2 \end{array}}$
$~$
${\begin{array}{rcl} (a - b)(a - b) &=&\\ &=& a^2 - ab - ab + b^2\\ &=& a^2 - 2ab + b^2 \end{array}}$
Difference of Two Squares
${\begin{array}{rcl} (a + b)(a - b) &=&\\ &=& a^2 - ab + ab + b^2\\ &=& a^2-b^2 \end{array}}$
-
Use the area model to simplify the expression.
Hints${ \begin{array}{rcl} (4y)^2 &=&\\ 4^2 \times y^2 &=& 16y^2 \end{array}}$
Draw the square and write the areas in the corresponding squares or rectangles.
SolutionIf you have a perfect square binomial such as $(x + a)^2$, you can approach this in two ways:
1.$~$Using FOIL
${\begin{array}{rcl} (x + a)^2 &=&\\ &=& (x + a)(x + a)\\ &=& x^2 + ax + ax + a^2\\ &=& x^2 + 2ax + a^2\\ ~\\ \end{array}}$
2.$~$Using the FOIL shortcut for Perfect Square Binomials
${ \begin{array}{rcl} ~\\ (x + a)^2 &=&\\ &=& x^2 + 2(ax) + a^2\\ \end{array}}$
$~$
${ \begin{array}{rcl} (x + 5)^2&=&\\ &=& x^2 + 2 \times 5x + 5^2\\ &=& x^2 + 10x + 25 \end{array}}$
$~$
${ \begin{array}{rcl} (3 + 3x)^2&=&\\ &=&3^2 + 2 \times 3 \times 3x + (3x)^2\\ &=& 9x^2 + 18x + 9 \end{array}}$
$~$
${ \begin{array}{rcl} (1 + 4y)^2&=&\\ &=&1^2 + 2 \times 1 \times 4y + (4y)^2\\ &=& 16y^2 + 8y + 1 \end{array}}$
$~$
${ \begin{array}{rcl} (2x + 4)^2&=&\\ &=&(2x)^2 + 2 \times 2x \times 4 + 4^2\\ &=& 4x^2+16x+16 \end{array}}$
-
Explain the FOIL method to Jack.
HintsHere you see an example for $(2x+4)^2$ using the area model. This corresponds to the FOIL method.
$(2x + 4)^2 = (2x)^2 + 2x(4) + 4(2x) + 4^2$
Remember, you have to apply the exponent to every term in the parentheses.
${ \begin{array}{rcl} (3y)^2 &=&\\ &=& 3y(3y)\\ &=& 9y^2 \end{array}}$
Look at this example for the FOIL method:
${ \begin{array}{rcl} (2a - b) &=&\\ &=& 2a(2a) + 2a(-b) + -b(2a) + -b(-b)\\ &=& (2a)^2 - 4ab + b^2 \end{array}}$
SolutionWe can expand the given perfect square binomial, $(5x-2y)^2$, using the FOIL method. First, we transform the expression:
${ (5x-2y)^2=(5x-2y)(5x-2y)}$
$~$
Let's start.
F multiply the first ${\large 5x(5x) = 25x^2}$
O multiply the outer ${\large 5x(-2y) = -10xy}$
I multiply the inner ${\large -2y(5x) = -10xy}$
L multiply the last ${\large -2y(-2y) = 4y^2}$
$~$
We still have to combine like terms.
${(5x - 2y)^2 = 25x^2 - 20xy + 4y^2}$
Party on, Jack!
-
Explain the FOIL method.
HintsYou can use the distributive property for ${ a(a-b)=a^2-ab}$ and for ${ -b(a-b)=-ab+b^2}$.
Here is another example.
SolutionWe can simplify ${ (a - b)^2 = (a - b)(a - b)}$ using FOIL multiplication.
For ${ (a + b)(a + b)}$, use the FOIL method:
F multiply the first ${ a \times a}$
O multiply the outer ${ a \times -b}$
I multiply the inner ${ -b \times a}$
L multiply the last ${ -b \times b}$
For the final step, we add all the resulting terms:
${ a^2 - ab - ab + b^2 = a^2 - 2ab + b^2}$
-
Simplify the following expressions.
HintsUse the formulas above and think about what to assign to $a$ as well as to $b$.
For example: $(2x-4)$.
You use the second formula with $a = 2x$ and b = 4$.
You can use those formulas also for calculating products of numbers
${ 22 \times 18 = (20 + 2)(20 - 2)}$.
Now we can plug in ${ a = 20}$ and ${ b = 2}$ in our third formula.
${ \begin{array}{rcl} 22 \times 18 &=& (a + b)(a - b)\\ &=& a^2 - b^2\\ &=& 20^2 - 2^2\\ &=& 400 - 4\\ &=& 396 \end{array}}$
SolutionThese formulas show a pattern to simplify the multiplication of special binomials.
Now, we'd like to practice using these formulas by substituting ${a}$ and ${ b}$ in the expressions:
First expression: $(12 - 3z)^2$
When ${ a = 12}$ and ${ b = 3z}$, we can use the second equation, ${(a + b)^2}$.${ \begin{array}{rcl} (12 - 3z)^2 &=&\\ &=& 12^2 - 2(12)(3z) + (3z)^2\\ &=& 144 - 72z + 9z^2 \end{array}}$
$~$
Second expression: $96 \times 104$
We should recognize that we can use the third formula:${ \begin{array}{rcl} 96 \times 104 &=& (a + b)(a - b) \end{array}}$
Substituting $a = 100$ and $b = 4$, we get:
${ \begin{array}{rcl} &=& (100 - 4)(100 + 4)\\ &=& (100 + 4)(100 - 4)\\ &=& 100^2 - 4^2\\ &=& 10000 - 16\\ &=& 9984 \end{array}}$
$~$
Third expression: $(1 + 9z)^2$
Using the second formula with $a = 1$ and $b = 9z$, we get:${ \begin{array}{rcl} (1 + 9z)^2 &=&\\ &=& 1^2 + 2(1)(9z) + (9z)^2\\ &=& 1 + 18z + 81z^2 \end{array}}$
$~$
Fourth expression: $(-3z - 4)^2$
Given the expression $(-3y - 4)^2$, we can use the first formula, but we have to remember to pay attention to the signs.Using $a = -3y$ and $b = -4$, we get:
${ \begin{array}{rcl} (-3z - 4)^2 &=&\\ &=& (-3z)^2 + 2(-3z)(-4) + (-4)^2\\ &=& 9z^2 - 24z + 16 \end{array}}$

Introduction to Polynomials – Naming Polynomials by Number of Terms

Adding Polynomials
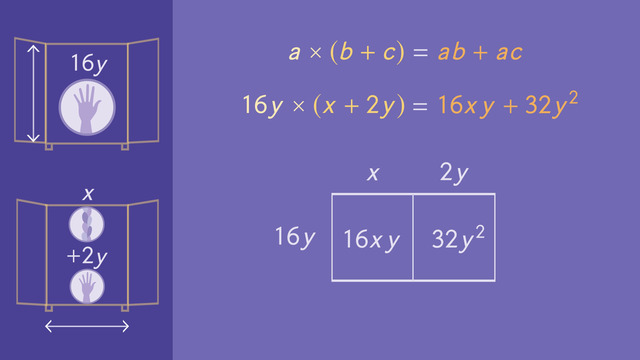
Multiplying Polynomials
Multiplying Special Case Polynomials

Factoring out the GCF

Factoring Trinomials with a = 1

Factoring Trinomials with a ≠ 1

Factoring Special Case Polynomials

Factoring by Grouping

Subtracting Polynomials











