Factoring by Grouping


Basics on the topic Factoring by Grouping
How do you factor a quadratic equation written in the standard form of ax² + bx + c when the a value is greater than 1? You can use a trick.
First, find factors of ac that sum to b. You may want to make a list. Next, write two new terms using the factors, and then group the four terms into binomials making sure when you factor out the greatest common factor, the second binomial is the same.
Let’s use an example: 2x² + 13x +15. Since ac is equal to 30, determine the factors of 30 that sum to the value of b which is 13. The factors are 3 and 10. Now modify the original equation to include the new terms 10x and 3x. The modified equation is 2x² + 10x + 3x + 15. Next, use parentheses to group: (2x² + 10)x + (3x +15). Factor out the GCF: 2x(x + 5) + 3(x + 5), and then write as a binomial pair: (2x + 3) (x + 5). Check your work by foiling.
As you continue to work with polynomials, you will notice there are a limited number of types of equations and if you learn to recognize the formats, factoring and solving becomes much easier. To see more examples of factoring of polynomials by grouping, watch this video.
Understand the relationship between zeros and factors of polynomials.
CCSS.MATH.CONTENT.HSA.APR.B.2
Transcript Factoring by Grouping
Adventure Mike and his girlfriend plan to build a treehouse. Using a snake as a measuring stick, Mike figured out the polynomial expression to represent the total area.
Oh jeez, his girlfriend just remembered – she wants a balcony, so she and Mike can watch the sunset. What can he do? She’s the romantic type. So, to save time, rather than measuring and calculating everything all over again, he can use grouping to factor polynomials.
Standard Form of a Quadratic Polynomial
Let’s take a look at the expression he wrote, 15x²+9x-6. Hmm. This looks familiar, doesn’t it? This expression is in the standard form of a quadratic polynomial, ax²+bx+c, but notice it's a trinomial and 'a' is equal to a number other than 1. To figure out the measurements for the sides of the treehouse, how can Mike factor this expression?
Multiplying Binomials
To show him how to factor by grouping, let’s use another problem as an example. To put this method into perspective, we'll start at the end result, with the factors. Working backwards, first, use the FOIL method to multiply the two binomials. Before combining like terms, we have 3x² + 6x – x – 2. To help you understand factoring by grouping, pay attention to the terms that are highlighted. After combining these like terms, the result is a trinomial in standard, quadratic form with 'a' equal to a number other than 1.
Finding the factored form
Let’s work on Mike’s problem. Okay, so how do you get from the standard form to the factored form when 'a' is not equal to 1? There's a little trick to doing this. We need to find the factors of 'ac' that sum to 'b'. a = 15 and c = -6. So since 'ac' = -90, here's a list of some of the factors of -90 – let's take a look. Hmm can you find the pair of factors that also sum to 9? That's right. -6 and 15 are factors of -90 and sum to 9.
Now, watch carefully while I do some mathemagic. Write two new terms using the factors of 'ac' that sum to 'b', and multiplied by 'x'.
Does this format look familiar? Remember the highlighted terms - from the example problem? Now to group, use parentheses to group the four terms into two binomials. This is a little tricky because you have to group the terms so that, when you factor out the GCF, the remaining binomial is the same for each. Also, be especially careful you don't make a sign error. Last step, combine the two GCFs, to create a new binomial. The polynomial is factored!
Adventure Mike has the measurements for the two sides of the treehouse. If his girlfriend wants a bigger treehouse, it won’t be a problem because he can just adjust the size of the sides.
Let’s fast forward, the treehouse is finally finished. To remember the special moment, Adventure Mike snaps some photos. Let's look Oh no! It seems like Mike has been alone in the jungle - just a little too long…
Factoring by Grouping exercise
-
Explain how to factor the given quadratic polynomial by grouping.
HintsTo factor quadratic polynomials by grouping, first multiply $a$ with $c$. Then sum all pairs of factors of this product and find the pair which sums to $b$.
Working backwards, we have:
$\begin{array}{rcl} (3x-1)(x+2)&=&3x(x+2)-(x+2)\\ &=&3x^2+6x-x-2 \end{array}$
SolutionIn order to factor such a quadratic polynomial,
$ax^2+bx+c$,
with $a$, $b$, and $c$ as coefficients, we must find all pairs of factors of $a\times c$.
Then we search for the pair of factors whose sum is $b$.
Let's have a look at an example: $3x^2+5x-2$.
Here we have $a=3$, $b=5$, and $c=-2$ and thus $a\times c=3\times -2=-6$.
The pairs of factors of $-6$ and their corresponding sums are:
$\begin{array}{rr|r} \text{factor}&\text{factor}&\text{sum}\\ \hline -1&6&5\\ 1&-6&-5\\ -2&3&1\\ 2&-3&-1 \end{array}$
The pair of factors which sums to $5$ is $-1$ and $6$.
The following grouping
$3x^2+5x-2=3x^2+6x-x-2$
then gives us
$3x(x+2)-(x+2)=(3x-1)(x+2)$.
which is the factorization we are looking for.
-
Factor the polynomial $15x^2+9x-6$.
HintsThe product of $15$ and $-6$ is $-90$.
You can write $-90$ as a product of two factors. Find the pair of factors that add up to $9$.
In the example,
$\begin{array}{rcl} (2x+3)(4x-2)&=&2x(4x-2)+3(4x-2)\\ &=&8x^2-4x+12x-6\\ &=&8x^2+8x-6 \end{array}$
we have that $8\times -6=48$, as well as $-4\times 12=48$. We can see that $-4+12=8$.
First multiply $a$ and $b$. Then we check all pairs of factors of $ab$ whose product is $ab$. If we add a pair of factors together and get $b$, then we've found the pair we are looking for.
SolutionTo factor the quadratic trinomial $15x^2+9x-6$ with $a=15$, $b=9$, and $c=-6$, we first look for the pairs of factors of $a\times c$ that sum to $b$.
We have that $a\times c=-90$, so we investigate all pairs of factors of $-90$:
${\small\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c} \text{Factors of }-90&-1,90&1,-90&-2,45&2,-45&-3,30&3,-30&-5,18&5,-18&-6,15&6,-15 \\ \hline \text{Sum of factors }&89&-89&43&-43&27&-27&13&-13&9&-9 \end{array}}$
The sum of the factors $-6$ and $15$ is $-6+15=9$. So this is the pair we want.
Next we group the quadratic polynomial as follows:
$15x^2+9x-6=15x^2-6x+15x-6$.
Grouping the binomials together, we get $(15x^2-6x)+(15x-6)$.
The greatest common factor of the left binomial is $3x$ and of the right binomial is $3$:
$(15x^2-6x)+(15x-6)=3x(5x-2)+3(5x-2)$.
Now we see that both summands have the binomial $5x-2$ as a common factor, and thus we can factor even further:
$3x(5x-2)+3(5x-2)=(3x+3)(5x-2)$.
-
Indicate the coefficients of the quadratic polynomials.
HintsKeep in mind that the $-$ sign belongs to the coefficient.
For the polynomial $3x^2+2x+4$, we have that $a=3$, $b=2$, and $c=4$.
Pay attention: Neiter $x^2$ nor $x$ belong to $a$ or $b$.
SolutionThe standard form of quadratic polynomial is given by
$ax^2+bx+c$, where $a\neq 1$.
Before we start to group quadratic polynomials we have to note the values of $a$, $b$, and $c$.
For the given polynomials, we look for the factor of the quadratic term $x^2$, $a$, the linear term, $b$, and the constant term, $c$:
- For $6x^2+x-2$, we have $a=6$, $b=1$, and $c=-2$.
- For $9x^2-25x-6$, we have $a=9$, $b=-25$, and $c=-6$.
- For $8x^2+4x-12$, we have $a=8$, $b=4$, and $c=-12$.
- For $8x^2+14x+3$, we have $a=8$, $b=14$, and $c=3$.
-
Factor the given polynomial.
Hints$ax^2+bx+c$ is the standard form of a quadratic polynomial.
For example, with $x^2-x+1$, we have that $a=1$, $b=-1$, and $c=1$.
Look for the pair of factors of $a\times c$ that sum to $b$.
Once you group a polynomial into two binomials, each binomial has a greatest common factor. So you can factor the greatest common factor from each binomial.
SolutionTo factorize the trinomial $6x^2+x-2$ we first look at the coefficients: Here we have $a=6$, $b=1$ and $c=-2$.
We're looking for the pairs of factors of $6\times (-2)=-12$ which sum to $1$.
$\begin{array}{rr|r} \text{factor}&\text{factor}&\text{sum}\\ \hline -1&12&11\\ 1&-12&-11\\ -2&6&4\\ 2&-6&-4\\ -3&4&1 \end{array}$
Now we can stop: We've found the factors $-3$ and $4$.
We can rewrite $6x^2+x-2$ as follows:
$6x^2+x-2=(6x^2-3x)+(4x-2)$.
Just look at the two resulting binomials in parentheses. The greatest common factor of the first one is $3x$ and of the second one is $2$:
$(6x^2-3x)+(4x-2)=3x(2x-1)+2(2x-1)$.
Now we see that both summands have the binomial $2x-1$ as a factor in common. So we factor to get, $3x(2x-1)+2(2x-1)=(3x+2)(2x-1)$.
The side lengths Adventure Mike was looking for are then $3x+2$ and $2x-1$.
-
Complete the following table of factors and sums.
HintsThe product of a pair of factors must be $-90$. If you know one factor, just divide $-90$ by that factor to get the other factor in the pair.
An example of a pair of factors of $-90$ and their sum:
SolutionFor $15x^2+9x-6$, we first multiply $15\times -6=-90$.
We then know that we are looking for all pairs of factors of $-90$, and one pair in particular which sum up to $9$.
Let's calculate the products and sums of all pairs of factors of $-90$:
- $-1\times 90=-90$ and $-1+90=89$
- $1\times (-90)=-90$ and $1-90=-89$
- $-2\times 45=-90$ and $-1+90=89$
- $2\times (-45)=-90$ and $2-45=-43$
- $-3\times 30=-90$ and $-3+30=27$
- $3\times (-30)=-90$ and $3-30=-27$
- $-5\times 18=-90$ and $-5+18=13$
- $5\times (-18)=-90$ and $5-18=-13$
- $-6\times 15=-90$ and $-6+15=9$
- $6\times (-15)=-90$ and $6-15=-9$
-
Consider the appropriate factorization.
HintsYou can either factor by grouping or use the FOIL method for binomials.
An example of the FOIL method:
$\begin{array}{rcl} (5x+1)(x+5)&=&5x^2+5x(5)+1x+1(5)\\ &=&5x^2+26x+5 \end{array}$
Remember: First, Outer, Inner, Last.
If you'd like to factor $ax^2+bx+c$ by grouping then:
- Find all pairs of factors of $a\times c$.
- Check which pair sums to $b$.
SolutionTo match the quadratic polynomial in standard form with its factorization, you can either factor the quadratic polynomial or multiply the binomials.
Let's go over how to use both methods with the polynomial $2x^2-11x+12$.
Factoring the Polynomial:
First we note that $a=2$, $b=-11$ and $c=12$.
First multiply $a$ and $c$ to get $2\times 12=24$.
Next look for the pair of factors of $24$ which sum to $-11$; the pair we are looking for is $-8$ and $-3$.
Then group to get $2x^2-11x+12=(2x^2-8x)-(3x-12)=2x(x-4)-3(x-4)$.
Then factor out the greatest common factors of the binomials to get $2x(x-4)-3(x-4)=(2x-3)(x-4)=(-2x+3)(-x+4)$.
Lastly, multiply each binomial with $-1$.
Multiplying the Binomials:
You can also use FOIL multiplication with $(3x-4)(2x-2)$.
We have that $(3x-4)(2x-2)=6x^2-6x-8x+8=6x^2-14x+8$.

Introduction to Polynomials – Naming Polynomials by Number of Terms

Adding Polynomials
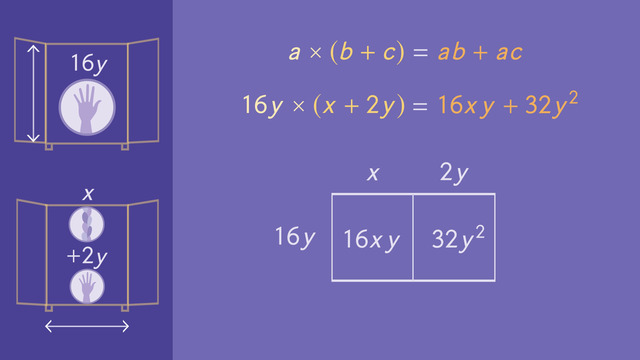
Multiplying Polynomials
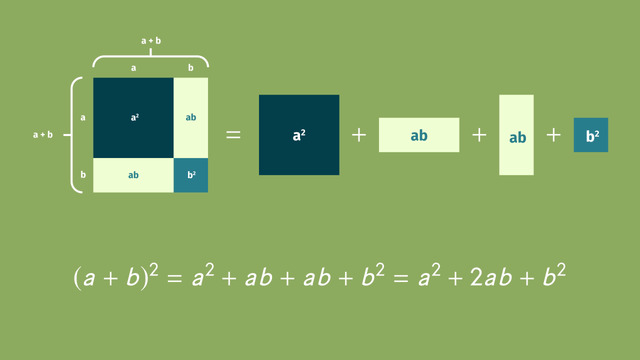
Multiplying Special Case Polynomials

Factoring out the GCF

Factoring Trinomials with a = 1

Factoring Trinomials with a ≠ 1

Factoring Special Case Polynomials

Factoring by Grouping

Subtracting Polynomials











