Multiplying Polynomials
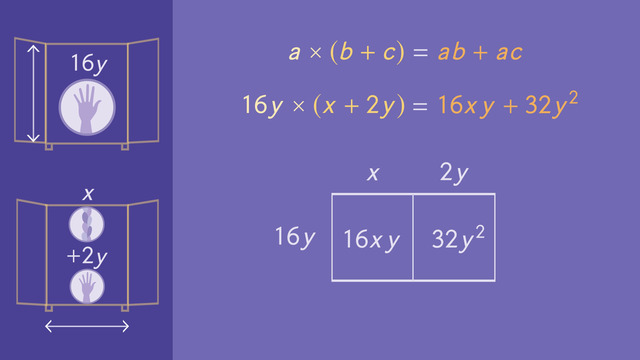

Basics on the topic Multiplying Polynomials
Summary of Multiplying Polynomials
Multiplying polynomials combines the laws of exponents for multiplication and adding polynomials.
To multiply two polynomials, we use the distributive property, [a(b +c + d) = ab + ac + ad], to make sure that each term of one polynomial is multiplied with every term of the other. Then, we add the results by combining like terms. There are different situations to consider:
- Multiplication of a Monomial by another Monomial
e.g. (5xy)(-2y) = -10xy² - Multiplication of a Monomial by a Polynomial
e.g. (-3x)(2x² - 5x + 1) = (-3x)(2x²) + (-3x)(-5x) + (-3x)(1) = -6x³ + 15x² - 3x - Multiplication of a Polynomial by another Polynomial
e.g. (x + 5)(-x² + 8x - 3) = (x)(-x²) + (x)(8x) + (x)(-3) + 5(-x²) + 5(8x) + 5(-3)
= -x³ + 8x² - 3x - 5x² + 40x - 15
= -x³ + 3x² + 37x - 15
For example, let's say that the length of a rectangular window is 5 feet more than its width, w². With this information we can write an algebraic expression for the area of the window: we have that its width = w² and its length = w² + 5. So the area of the rectangular window = w²(w² + 5) = w⁴ + 5w².
Perform arithmetic operations on polynomials.
Common Core
CCSS.MATH.CONTENT.HSA.APR.A.1
Let's practice: multiplying polynomials Exercises
With the following exercises on the topic of multiplying polynomials, you can test whether you have understood everything. Test your knowledge now!
Transcript Multiplying Polynomials
”Stuck in her tower, watchin' the hours pass,
MC Prince's gonna be put on blast.
For makin' Rap wait, that ain't cool,
ensconced in the tower like a fool,
With no tools, no hope and no measure,
an empty room gives a girl no pleasure”
”Her hands, her thumbs 'n that hair is what she'll apply
to the situation she needs to rectify,
...to deck out her room with some fly gear
b'fore she goes crazy like King Lear
For a sick new room to make her feel jovial,
Rap's gotta know how to multiply polynomials”
Defining the unkown quantities
Let's help Rap-Punzel measure her room using her long locks as a measuring tool. The dimensions of her rectangular room are eight times the length of the section of her hair that she uses to measure. The length of her hair is an unknown quantity; we’ll call this 'x'. The length of her room is 40 times the width of her hand. The width of her hand is another unknown quantity, which we'll call 'y'.So, the width of the room is 8x, and the length of the room is 40y.
Do you remember how to calculate the area of a rectangle? Of course you do! You multiply the length times the width. To figure out the area of Rap-Punzel's room, multiply the two monomials. 8x(40y). 8(40) = 320, and x(y) = xy, so the product of the two monomials is 320xy. Next, Rap-Punzel measures the closet. The length is 16 times the width of her hand, or 16y. The width is 1 times the length of her hair plus 2 times the width of her hand, giving us the binomial x + 2y.
Multiplying Polynomials
Again, find the area by multiplying, but this time you multiply a monomial by a binomial. Let’s work this out. To do this, you can use the Distributive Property. Remember the Distributive Property? a(b+c) = ab + ac? You can apply this property to numbers, variables and polynomials. For this expression, a = 16y, b = x, and, c = 2y.
Now solve by distributing the 16y to the two terms that are summed inside the parentheses, so the resulting binomial is 16xy + 32y². You can also set this expression up using an area model created with one row and 2 columns. The row is labeled 16y, and 2 columns are labeled x and 2y to model the x plus 2y. Multiply the row times each column to calculate the area of each of the rectangle's sections. The area of the first rectangle is 16xy, and the area of the second is 32y². Add them together and you get the same answer as before, 16xy + 32y².
Rap-Punzel uses the width of her hand and also her thumb to measure the length and width of her magical mirror. The length of the mirror is 8 times her hand and 7 times her thumb. She knows her thumb is about an inch wide. The width then, is 6 times her hand and 5 times her thumb.
FOIL Method
We can use a special method to calculate the area of the magical mirror. This method, the FOIL method, works only when you multiply two binomials. To FOIL, multiply the first two terms of each binomial. Next, multiply the outer terms of each binomial. Then, multiply the inner terms and last, multiply the last terms. Check it out!? It kind of looks like a claw! Let’s try it out using the measurements of the mirror. First, 8y(6y) = 48y². Outer, 8y(5) = 40y. Inner, 7(6y) = 42y and Last, 7(5) = 35. Combine the like terms and rewrite the terms in the standard form, listing the exponents in order from greatest to least. 48y² + 82y + 35.
Area Model
There's another method to solve this. You can also use the area model. This time, the area model is set up using 4 rectangles, to represent each of the four terms in the two binomials. The four rectangles are arranged in 2 rows and 2 columns. To find the products, multiply the rows by the columns to find each area, add the like terms, and write the result in standard form. Using the area model, what's the product of the two binomials? Just the same as before: 48y² + 82y + 35.
Multiplying trinomials by binomials
Lastly, Rap-Punzel measures her bed. The width of the bed is 2 hair lengths minus 2 hand widths plus 3 thumbs, and the length is 7 hand widths plus 5 thumbs. A trinomial times a binomial?! What can Rap-Punzel do to figure out the area of the bed? She can’t FOIL because you only use the FOIL method to multiply two binomials, but she can use the always-dependable Distributive Property.
Let’s distribute! Again, use the Distributive Property as your guide to rewrite the expression. Multiply the trinomial by the first term of the binomial, 7y, and then multiply the trinomial by the second term of the binomial, 5. Now add both of the results together. As always, write it in standard form. You can also use the area model; this time, set it up with 3 rows and 2 columns. Watch out for the negative signs when you calculate the area for each rectangular section and also when you combine like terms. Just like before, the product of the two polynomials is -14y² + 14xy + 11y + 10x + 15.
”With her room all done and er'thing in its place,
Rap moves the mirror to reveal a space,
A hole in the wall, what a trip
time to escape and begin her courtship,
of Prince MC, oh where can he be?”
In the tower, that's where...eh, c'est la vie!
Multiplying Polynomials exercise
-
Multiply two binomials using the FOIL method.
HintsFOIL stands for:
Multiply the First,
Multiply the Outer,
Multiply the Inner, and
Multiply the Last.
Here is an example for multiplication using the FOIL method:
Remember to combine like terms.
SolutionWe use the FOIL method for multiplying:
$(8y+7)\times(6y+5)=...$
Multiply the First: $\rightarrow$ $(8y)(6y)=48y^2$
Multiply the Outer: $\rightarrow$ $(8y)(5)=40y$
Multiply the Inner: $\rightarrow$ $(7)(6y)=42y$
Multiply the Last: $\rightarrow$ $(7)(5)=35$
Lastly, add all the terms together and combine the like terms. We then get:
$\begin{array}{rcl} (8y+7)\times(6y+5)&=&48y^2+40y+42y+35\\ &=&48y^2+82y+35 \end{array}$
-
Determine the area of Rap-Punzel's closet.
HintsThe distributive property helps us with multiplying a monomial by a binomial:
In the following picture, we see how to calculate the area of a rectangle:
SolutionFirst we assign the variable $x$ to represent the length of Rap-Punzel's hair, and $y$ to represent the length of her hand.
The height of her closet is then given by $16y$ and the width is then given by $x+2y$.
We get the area by multiplying the height by the width of the closet, like so: $(16y)\times (x+2y)$.
Using the distributive property, we get that the area of her closet is $16xy+32y^2$.
-
Calculate the area of the bed using the area model.
HintsFor each row, multiply the monomial for that row with the monomial of each column.
Pay attention to the signs of terms.
Lastly, add all terms together and combine like terms.
SolutionYou can see how to use the area model to solver our problem in the following picture.
Let's check the picture line by line:
- First line: $2x\times6y=12xy$ and $2x\times 9=18x$
- Second line: $y\times 6y=6y^2$ and $y\times 9=9y$
- Third line: $-2\times 6y=-12y$ and $-2\times 9=-18$
$12xy+6y^2+18x+9y-12y-18=12xy+6y^2+18x-3y-18$.
Lastly we arrange this result from largest degree to smallest,
$6y^2+12xy+18x-3y-18$.
-
Check the area model for the given products.
HintsDon't forget about the sign!
Here is an example for $(x+y)\times(x+y)$:
Solution- First: $(2x-3)\times(3x+2)$.
Lastly, we add the terms and combine like terms to get
$6x^2+4x-9x-6=6x^2-5x-6$
$~$
- Second: $(3x+4y)\times (2-3y)$.
We add up the terms to get
$6x-9xy+8y-12y^2=-12y^2-9xy+6x+8y$.
$~$
- Third: $(6-4x)\times (4x-3)$.
Adding the terms and combining like terms gives us
$24x-18-16x^2+12x=-16x^2+36x-18$.
$~$
- Fourth: $(y+x)\times (4x+2y)$.
Lastly we add the terms and combine like terms to get
$4xy+2y^2+4x^2+2xy=4x^2+2y^2+6xy$
-
Decide which statements are true about the FOIL method.
HintsHere is an example for the distributive property:
A monomial is a single term; for example $3x$.
An example of a binomial is $3x-4y$, which is composed of two monomials.
A trinomial is composed of three monomials, like $3x-4y+4$.
Here is an example of the FOIL method with $(8y+7)\times (6y+5)$:
SolutionThe FOIL method only works for two binomials.
$~$
Let's have a look at an example:
$(8y+7)\times(6y+5)=...$
F multiply the first $(8y)(6y)=48y^2$
O multiply the outer $(8y)(5)=40y$
I multiply the inner $(7)(6y)=42y$
L multiply the last $(7)(5)=35$
$~$
If we only have two monomials we don't have inner or outer terms.
$~$
To multiply a monomial with a binomial we use the distributive property. For example, $8y\times(6y+5)=48y^2+40y$.
-
Solve the following products.
HintsAs seen in the following example, to multiply two monomials multiply the coefficients:
If you have to multiply a binomial by a monomial, use the distributive property:
You can use the FOIL method to multiply two binomials:
Multiply the First,
Multiply the Outer,
Multiply the Inner, and
Multiply the Last.
You can also use the area model; it all depends on your preference.
Solution1. $3y\times 4y=3\times 4\times y\times y=12y^2$.
$~$
2. To multiply a monomial with a binomial, use the distributive property:
$3y\times (4y+3)=3y\times 4y+3y\times 3=12y^2+9y$
$~$
3. Use the FOIL method for $(4x-3)\times (2x+y)$:
- Multiply the First $4x\times 2x=8x^2$.
- Next multiply the Outer $4x\times y=4xy$.
- Now multiply the Inner $3\times 2x=6x$.
- Last multiply the Last $3y$.
$~$
4. Lastly we multiply a monomial with a trinomial,
$4x\times(2x+3y-4)$.
We use the distributive property two times:
$\begin{array}{rcl} 4x\times(2x+3y-4)&=&4x\times(2x+3y)+4x\times (-4)\\ &=&4x\times 2x+4x\times 3y-16x\\ &=&8x^2+12xy-16x. \end{array}$

Introduction to Polynomials – Naming Polynomials by Number of Terms

Adding Polynomials
Multiplying Polynomials
Multiplying Special Case Polynomials

Factoring out the GCF

Factoring Trinomials with a = 1

Factoring Trinomials with a ≠ 1

Factoring Special Case Polynomials

Factoring by Grouping

Subtracting Polynomials










PLZZZZZ MORE RAPUNZEL VIDS!!!!!
RAPunzel do some more
I love the rap, but plz… WORK ON YO BARS!!!!