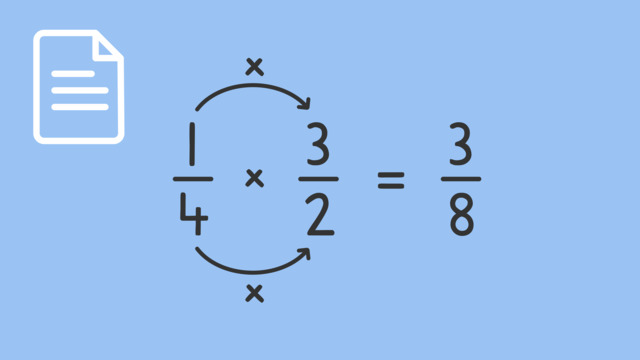Multiplying Fractions Less than 1
- Multiplying Fractions Less than One
- Understanding Fractions – Definition
- How Do We Multiply Fractions?
- Multiplying Fractions Less than One – Practice
- Multiplying Fractions Less than One – Real World Application
- Multiplying Fractions Less than One – Summary
- Multiplying Fractions Less than One – Frequently Asked Questions
Learning text on the topic Multiplying Fractions Less than 1
Multiplying Fractions Less than One
When you're sharing a delicious pie or measuring ingredients for baking cookies, you're often working with fractions to describe less than a whole. Understanding how to multiply fractions that are smaller than one is especially useful in the kitchen or when dividing an object into smaller sections. Learning to multiply fractions is an important skill that can help you in practical situations.
Understanding Fractions – Definition
Fractions represent parts of a whole item or a set. They consist of a numerator, the number above the fraction bar, and a denominator, the number below the fraction bar. The numerator tells us the number of parts we have, and the denominator tells us how many of those parts are needed to make up a whole.
How Do We Multiply Fractions?
Multiplying fractions involves multiplying the numerators together, and doing the same with the denominators. This combines the parts to give a new fraction.
Simplifying fractions before you multiply them can make the numbers smaller and easier to work with, which makes solving the problem faster and less confusing! It's like cutting up your food into smaller pieces before eating—it makes the task much easier to handle.
Suppose you need to multiply $\frac{4}{6}$ and $\frac{9}{12}$.
Simplify each fraction first: * $\frac{4}{6}$ simplifies to $\frac{2}{3}$ (since both 4 and 6 can be divided by 2). * $\frac{9}{12}$ simplifies to $\frac{3}{4}$ (since both 9 and 12 can be divided by 3).
Now multiply the simplified fractions: * $\frac{2}{3} \times \frac{3}{4} = \frac{6}{12}$, which then simplifies to $\frac{1}{2}$.
By simplifying the fractions first, you deal with smaller numbers, making the multiplication easier and quicker!
Multiplying Fractions Less than One – Practice
Let's work through some guided examples together:
Multiplying Fractions Less than One – Real World Application
Let's practice how multiplying fractions can be applied to everyday situations, such as adjusting recipes. This skill helps you modify quantities accurately according to your needs.
Multiplying Fractions Less than One – Summary
Key Learnings from this Text:
- Multiplying fractions involves multiplying the numerators together and the denominators together.
- The result of multiplying two fractions less than 1 is a smaller fraction, also less than 1.
- Simplify your answer if possible to make it easier to understand and use.
- Applying multiplication of fractions to real-life scenarios can reinforce understanding and proficiency.
Explore more about fractions and other mathematical concepts here to become a fractions expert!