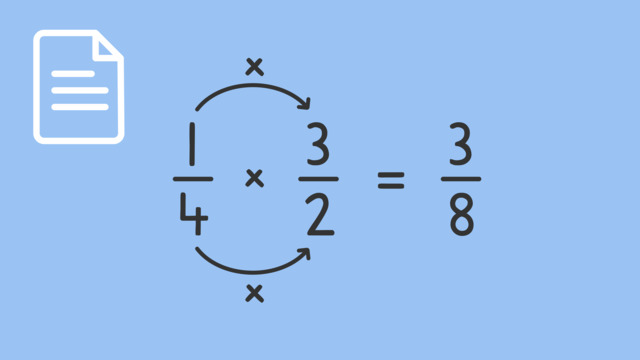Dividing Whole Numbers by Unit Fractions Using Models
- Dividing Unit Fractions by Whole Numbers
- Dividing Unit Fractions by Whole Numbers Explanation
- How to Divide Fractions by Whole Numbers
- Dividing Unit Fractions by Whole Numbers – Example
- Dividing Unit Fractions by Whole Numbers— Guided Practice
- Dividing Unit Fractions by Whole Numbers – Application
- Dividing Unit Fractions by Whole Numbers – Summary
- Dividing Unit Fractions by Whole Numbers – Frequently Asked Questions


Basics on the topic Dividing Whole Numbers by Unit Fractions Using Models
Dividing Unit Fractions by Whole Numbers
Dividing unit fractions by whole numbers is an important concept in 5th-grade mathematics. Understanding this process builds on the already obtained division and fraction knowledge and is crucial for developing strong foundational skills in working with rational numbers, such as Ordering Rational Numbers.
A unit fraction is a fraction where the numerator (top number) is 1, and the denominator (bottom number) is a whole number. Examples include $\frac{1}{2}$, $\frac{1}{3}$, and $\frac{1}{4}$.
Dividing Unit Fractions by Whole Numbers Explanation
When we divide a unit fraction by a whole number, we find out how many of those fractions fit into one part of the whole. This process can be thought of as splitting a unit fraction into smaller, equal parts as identified by the whole number.
How to Divide Fractions by Whole Numbers
There are logical steps you can take to divide unit fractions by whole numbers.
- Identify the Fraction and the Divisor: Identify the unit fraction and the whole number you're dividing by.
- Divide the Fraction: Divide the unit fraction into as many equal parts as the whole number indicates.
- Determine the New Fraction: Each part of the split unit fraction becomes a smaller unit fraction, because you’re dividing the unit fraction into smaller, equal parts.
It is important to understand that when dividing a unit fraction by a whole number, your answer will be smaller than what you started with. This means the new denominator will be a bigger number as a result.
Dividing Unit Fractions by Whole Numbers – Example
Let's explore this concept with a detailed example.
Example 1: Dividing $\frac{1}{4}$ by 3
Identify the Unit Fraction and Divisor:* The unit fraction is $\frac{1}{4}$ and the divisor is the whole number 3.
Divide the fraction: Imagine a pie cut into 4 equal parts. Take one of these parts ($\frac{1}{4}$). Now divide this $\frac{1}{4}$ into 3 further equal parts.
Determine the new fraction: Each of these new parts is a smaller fraction of the original quarter piece. After dividing, each of the 3 smaller sections is $\frac{1}{12}$ of the whole pie.
Dividing Unit Fractions by Whole Numbers— Guided Practice
This time, we will walk through the steps together to divide $\frac{1}{8}$ by 3.
Dividing Unit Fractions by Whole Numbers – Application
Let’s apply what we’ve learned with some exercises:
Dividing Unit Fractions by Whole Numbers – Summary
Key Learnings from this Text:
Dividing unit fractions by whole numbers helps us understand how to split a fraction into smaller, equal parts.
The result of this division is always a smaller unit fraction.
Visualization tools like pie charts and fraction bars can aid in understanding this concept.
Here are the steps you should follow in a simple table:
| Step | Description | Example: Dividing $\frac{1}{8}$ by 3 |
|---|---|---|
| 1. Identify the Fraction and Divisor | Start with a unit fraction and the whole number you're dividing by. | Unit Fraction: $\frac{1}{8}$, Divisor: 3 |
| 2. Visualize the Division | Imagine a visual representation of the fraction. | Picture a cake cut into 8 equal slices. Focus on one slice $\frac{1}{8}$. |
| 3. Divide the Fraction Further | Divide the unit fraction into as many equal parts as the number indicates. | Divide the $\frac{1}{8}$ slice of the cake into 3 smaller, equal parts. |
| 4. Determine Each New Part | Each new part represents a smaller fraction of the whole. | Each part is $\frac{1}{24}$ of the entire cake. |
Continue practicing this concept by exploring Dividing Whole Numbers by Unit Fractions Using Models.
Dividing Unit Fractions by Whole Numbers – Frequently Asked Questions
Dividing Whole Numbers by Unit Fractions Using Models exercise
-
What does each keyword mean?
HintsA fraction contains a numerator and a denominator. Which is the top and which is the bottom?
Examples of unit fractions are
$\frac{1}{3} , \frac{1}{5} , \frac {1}{2} , \frac{1}{10}$
What do you notice about these?
A cake is split into six equal slices, the splitting is called division and the individual slices are fractions of the cake.
SolutionA fraction is a part of a whole.
A numerator is the top number in a fraction.
A denominator is the bottom number in a fraction.
Division is sharing or splitting a number into equal parts.
A unit fraction is a fraction where the numerator is one.
-
How many quarters are there in three chocolate bars?
HintsThe model should represent the question. First, check how many chocolate bars are in the question.
Next, check how many pieces each bar is cut into. The denominator of the unit fraction tells you this.
Finally, count the number of pieces in total.
SolutionHere we can see the correct answer.
There are three chocolate bars split into quarters (four pieces). Counting the pieces gives 12 pieces, therefore, the answer is $3 \div \frac{1}{4} = 12$.
-
Dividing a whole number by a unit fraction.
HintsThe first number tells us how many items there are.
The denominator of the unit fraction tells us how many parts the item is split into.
Two cakes split into four equal slices would be represented by the math sentence $2 \div \frac{1}{4} = 8$
SolutionThe image shows the correct solutions.
Sweets: $3 \div \frac{1}{4} = 12$
Chocolate bars: $2 \div \frac{1}{6} = 12$
Pizza: $4 \div \frac{1}{3} = 12$
Muffins: $6 \div \frac{1}{2} = 12$
-
Divide the whole numbers by the unit fraction.
HintsWhen dividing a whole number by a unit fraction we are counting how many times the fraction is in the whole.
When dividing a whole number by a unit fraction the quotient will always be a number greater than the whole number you started with.
If you have five pizzas and divide each pizza in half, how many slices would you have?
SolutionIn the image we can see the first solution:
$\bf{5 \div \frac{1}{2} = 10}$ because there are $2$ equal pieces in each of the $5$ wholes.
--------------------------------------------------------------------------------------------
$\bf{4 \div \frac{1}{4} = 16}$ because there are $4$ equal pieces in each of the $4$ wholes.
$\bf{9 \div \frac{1}{3} = 27}$ because there are $3$ equal pieces in each of the $9$ wholes.
$\bf{6 \div \frac{1}{3} = 18}$ because there are $3$ equal pieces in each of the $6$ wholes.
-
How many quarters are there in two cakes?
HintsEach cake is represented by one whole. There are two whole cakes.
The denominator tells us how many equal pieces the cakes are split into. In the image we can see that each cake has been split into four equal pieces.
Another way to read the question is - the two cakes are divided into quarters, how many pieces are there?
Look at the image for a similar question. There are $3$ muffins, the whole number is written first. It is divided into thirds, the fraction is written after the division sign.
SolutionThe correct maths sentence is $2 \div \frac{1}{4}$ because there are two cakes each divided into quarters.
There are $\bf{8}$ quarters in the two cakes.
-
Five cakes are cut into thirds. How many slices are there?
HintsThere are five cakes, this is your whole number.
Each cake is split into equal slices. The denominator of the unit fraction tells you how many equal slices.
Each cake has three equal slices.
SolutionYou have five cakes, each one is split into thirds.
This means that each of the five cakes is split into three slices. There are $\bf{15}$ slices in total.
$5 \div \frac{1}{3} = 15$