Adding 3 Digit Numbers Using Standard Algorithm
- Adding Three-Digit Numbers
- What Are Three-Digit Numbers? – Introduction
- Foundational Steps to Add Three-Digit Numbers
- Step-by-Step Guide to Three-digit Addition with Carrying Over
- Adding Three-Digit Numbers – Common Mistakes
- Adding Three-Digit Numbers – Conclusion
- Adding Three-Digit Numbers – Frequently Asked Questions


Basics on the topic Adding 3 Digit Numbers Using Standard Algorithm
Adding Three-Digit Numbers
Three-digit numbers are integral in various mathematical calculations and daily applications. If you're looking for resources and strategies to help your child or student with three-digit addition, you've come to the right place! We offer a variety of tools and tips to make learning three-digit addition a breeze. Read our educational text about three-digit numbers, refer to the three-digit addition video and apply your knowledge by using our 3 digit addition math worksheets.
What Are Three-Digit Numbers? – Introduction
Three-digit numbers range from 100 to 999.
Three-digit numbers are never smaller than 100 and never greater than 999. Each number has three digits: one in the hundreds place, one in the tens place, and one in the ones or units place.
Place value is crucial when working with three-digit numbers, as it informs us of a digit's value. Recognizing the hundreds, tens, and ones place is vital for performing calculations like addition with three digits correctly. Let’s have a look at the number 367 in a place value chart. The digits are placed in the hundreds (H), tens (T) and ones place (O):
| H | T | O |
|---|---|---|
| 3 | 6 | 7 |
Foundational Steps to Add Three-Digit Numbers
Once pupils understand three-digit numbers, they can begin learning how to add them. There are essential steps to simplify the process. Three-digit numbers can be difficult to add, so always use a place value chart or use a standard written method to add three-digit numbers.
1. Prepare for your calculation
Write down the numbers in a standard written format, aligning digits according to their place value.
2. Always start with the ones place
Begin by adding the digits in the ones place. If the sum is a two-digit number, write down the digit in the ones place and carry over the ten to the tens place.
Understanding carrying over in addition Carrying over is a fundamental concept when the sum in the ones and tens place is a two-digit number. It involves adding the carried-over number to the sum of the digits in the next place.
3. Move on to adding tens
Once you added the unit digits, move on to adding the digits in the tens place. Do not forget to also add any numbers that you carried over from adding the unit digits. If the sum is a two-digit number, write down the unit and carry over the ten to the hundreds place.
4. Move on to adding hundreds
Once you added the digits in the tens place, move on to adding the digits in the hundreds place. Do not forget to also add any numbers that you carried over from adding the tens digits. If the sum is a two-digit number, write down the sum in the hundreds and thousands place.
Step-by-Step Guide to Three-digit Addition with Carrying Over
Let’s look at the example equation and do it together, step by step. Let’s complete 391 + 139. 1. Prepare for your calculation
Write down the first number 391, and right underneath it 139, in a standard written format. Align digits according to their place value - make sure that 9 is under 1, 3 under 9, and 1 under 3. See the example below:
2. Always start with the ones place
Begin by adding the digits in the ones place. In this case, we will add 9 and 1. As you know, the sum of these two digits is 10. This means that you will have to write down 0 in the ones place and carry 1 ten over.
Understanding Carrying Over in Addition Carrying over is a fundamental concept when the sum in the ones and tens place is a two-digit number. It involves adding the carried-over number to the sum of the digits in the next place.
3. Move on to adding tens
Once you added the unit digits, move on to adding the digits in the tens place. Here we will need to add 3 tens and 9 tens. However, let’s not forget that there is one more ten that we carried over from the unit's place. In this case, 3 plus 9 plus 1 equals 13. As this sum is over 10, we will have to carry over again. See the example below:
4. Move on to adding hundreds
Once you added the digits in the tens place, move on to adding the digits in the hundreds place. Here we 1 hundred and 3 hundred, their sum equals 4 hundred. But do not forget to also add the 1 hundred we carried over from the tens column! Write the digit 5 in the hundreds place. Well done, you have added two three-digit numbers and their sum is 530 - five hundred and thirty. Look at the representation below:
Adding Three-Digit Numbers – Common Mistakes
Common errors include forgetting to carry over or carrying over incorrect values. Also, pay attention to zeros in the ones or tens place. It is important to never skip them and always remember to keep them as place value holders. Practice and attention to detail can help avoid these mistakes.
Adding Three-Digit Numbers – Conclusion
Mastering the addition of three-digit numbers is essential for students, as it lays the groundwork for more advanced mathematical concepts and applications. With understanding, practice, and the use of available resources, students can efficiently and accurately add three-digit numbers. Consistent practice and engagement with various learning tools and materials will facilitate mastery of this fundamental skill.
The key steps to successful three-digit addition are:
| Step # | What to do |
|---|---|
| 1 | Prepare for your calculation |
| 2 | Always start with the ones place |
| 3 | Move on to adding tens |
| 4 | Move on to adding hundreds |
Adding Three-Digit Numbers – Frequently Asked Questions
Transcript Adding 3 Digit Numbers Using Standard Algorithm
Mr. Squeaks is taking off on the trip of a lifetime! He is going to visit a magical place that his beloved grandpa used to tell him stories about. He’s so excited about this trip and has never traveled this far, so he wants to record every moment in his journal! We can help figure out how far away his destination, is by totaling up the distance he travels each day. "Adding Three-Digit Numbers Using Standard Algorithm" Let’s look at Mr. Squeaks’ flight log to calculate how far he traveled. To find the total distance, we’ll start with his travel of day one and day two combined. First, set up the problem by writing one hundred forty-two(...) over one hundred twenty-six. Make sure to include the addition sign, so we remember the operation. Start with the ones place. (...)what is two plus six? We put the eight directly underneath this place value. Move to the left and look at the tens place. How many tens are there in forty and twenty? There are SIX TENS in the number sixty. Write the digit six in the tens place, directly below the line. Continue moving left to the hundreds place. Even though you see the digit one, these have the value of one hundred. We say one hundred plus one hundred equals two hundred. In the answer, we write a two under the hundreds column. WOW! So far Mr. Squeaks has traveled two hundred, sixty-eight FEET! The next day he continues another one hundred and twenty-three feet. Let’s add that to our travel log. For our next problem, we have two hundred, sixty-eight and one hundred twenty-three. We have the eight over the three in the ones place,(...) the six over the two in the tens(...) and the two over the one for the hundreds. Again, we want to go back over to the ones place to start adding. Eight and three more, make eleven. What error do you notice in this answer? ...We can not have two digits in one place value. This ONE would be REGROUPED to the tens place. There are now three digits to add in the tens column. We add the tens by starting with the numbers that we already have in the problem. Six tens plus two tens make eight tens(...)and now we add one more group of ten. We have ninety, or NINE TENS. Since we don’t have to regroup, we move over to add the hundreds place. Two hundred and one hundred equals three hundred. In all, he has gone three hundred, ninety-one feet! Mr. Squeaks is almost to his destination(...)one more day to travel! On his final day, he adds another one hundred thirty-nine feet. Pause the video and try this one on your OWN before we go over it. What did you notice about the regrouping when solving this problem? We had to regroup TWICE(...)both in the tens and hundreds place. Let’s take a look at how we added up these numbers. Starting at the ones place, one plus nine makes ten. What digit do we write underneath the ones place? Zero(...) because there are zero ones in the number ten. The one moves over to the tens place and is added in with nine and three(...) for a total of thirteen tens. Thirteen tens is the same as having one hundred and three tens, so we regroup again. In the hundreds place, we add(...) three hundred and one hundred and one hundred more. The sum is five hundred, so we put a five in the hundreds place. MR. SQUEAKS HAS TRAVELED FIVE HUNDRED AND THIRTY FEET!! Remember(...) in standard algorithm, we line up numbers vertically, or one top of the other, based on place values... We start by adding with the ones place(...) and move to the left to add the tens(...) and again to add the hundreds. Sometimes we need to regroup into the next place value when our sum is greater than ten. Mr. Squeaks steps off the plane. It was the most BEAUTIFUL thing he had ever seen! His grandpa would be SO PROUD! [Mr. Squeaks lands steps off the plane and walks towards the most beautiful sight. Then we see the World's Largest Hamster Wheel (maybe with a glowing light behind it) He looks down at his photo and he looks back up. He has a huge smile on his face. The video ends with side-by-side pictures of his trip and his grandpa's. ]
Adding 3 Digit Numbers Using Standard Algorithm exercise
-
What is the place value of the underlined digit?
HintsPut your number in the columns below.
Is the underlined digit in the hundreds, tens or ones column?
SolutionIf your number has 3 digits it will have a hundreds, tens and ones place.
3 0 6 Tens
3 hundreds 0 tens 6 ones
2 7 1 Hundreds
2 hundreds 7 tens 1 one
9 8 1 Ones
9 hundreds 8 tens 1 one
-
Can you find the mistake in the solution?
HintsMake sure the answers have been placed in the correct columns.
Since the answer from the tens column is more than 2 digits, we need to carry the tens number over to the hundreds column.
SolutionFor the ones place: 3 + 5 = 8
For the tens place: 4 + 7 = 11
We need to regroup the digit in the tens place to the hundreds column. So you are left with a 1 in the tens place.
For the hundreds place: 1 + 2 + 2 = 5
500 + 10 + 8 = 518
-
Solve the equation by placing the digits into the correct boxes.
HintsFirst, make sure you have put all of the digits for the number you're adding in the correct place.
Start by adding the ones, then the tens, and lastly the hundreds place.
Don't forget if your answer in the ones or tens column is greater than 9, you need to regroup the digit in the tens of the number to the next column.
SolutionOnce the digits are in the correct column:
- Add the ones column first. 4 + 3 = 7.
- Then add the tens column. 4 + 6 = 10. We need to regroup the 1 to the hundreds column. So we're left with a 0 in the tens column.
- Finally add the hundreds column. 1 + 3 + 2 = 6.
-
Solve the equations.
HintsFor this example, looking at the answer in the tens column, the 1 in 12 needs to be regrouped to the hundreds column. Then, the hundreds column will be 1 + 7 + 6.
Are there any that need to be regrouped for these equations above?
Start adding the ones place first.
Then add the tens place.
Finally add the hundreds place.
Solution473 + 326 = 799
306 + 291 = 597
651 + 367 = 1,018
-
What's the solution?
HintsAdd the digits in the ones column first.
3 + 5 =
Add the digits in the tens column next.
4 + 2 =
SolutionAdd the digits in the ones column first 3 + 5 = 8
Then add the digits in the tens column 4 + 2 = 6
Finally add the digits in the hundreds column 2 + 1 = 3
243 + 125 = 368
-
Solve the answers to the equations.
HintsPut the numbers on top of each other in the place value chart. Make sure all digits are in the correct column.
SolutionPut the numbers on top of each other in the place value chart.
Add the digits in each column, starting with the ones, then tens, and lastly, hundreds.
For 362 + 244:
Add the ones: 2 + 4 = 6
Then add the tens: 6 + 4 = 10 We need to regroup the 1 to the hundreds column.
Lastly, add the hundreds: 1 + 3 + 2 = 6
362 + 244 = 606
______________________________
For the rest of the equations:
271 + 149 = 420
745 + 639 = 1384
549 + 207 = 756
365 + 256 = 621

Adding a 1-Digit Number to a 2-Digit Number

Order in Adding
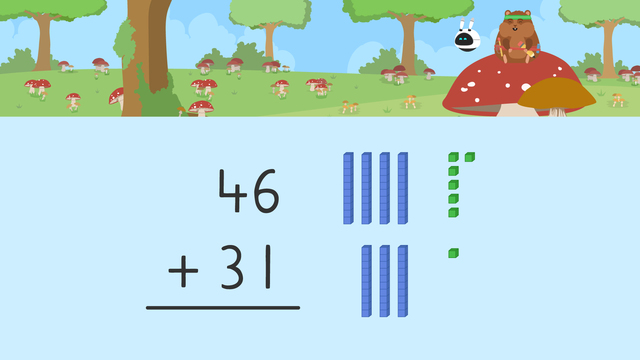
Using Place Value to Add
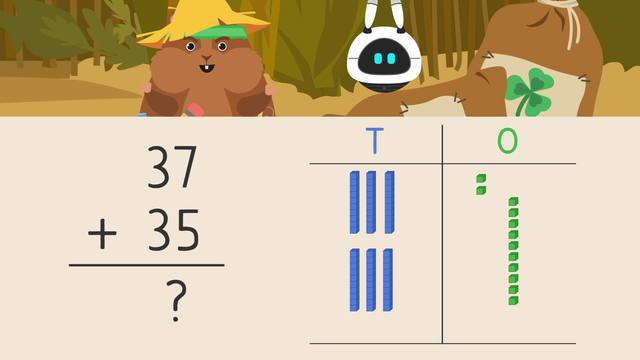
Using Place Value to Add Two Digit Numbers (Regrouping)
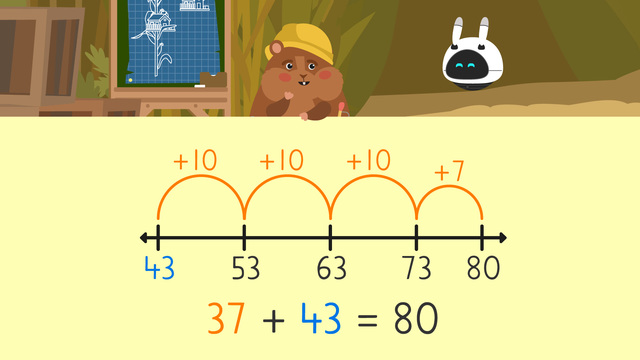
Make a Number Line to Add

Make a Number Line to Add — Let's Practice!
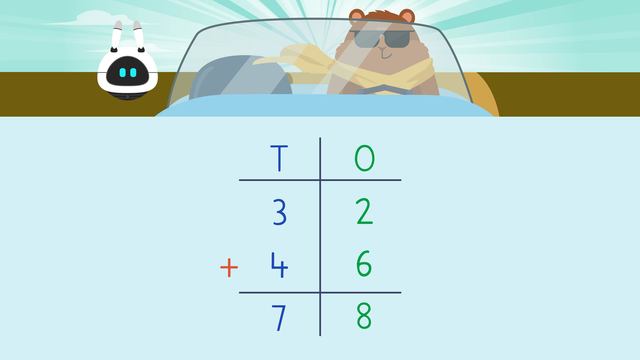
Addition Using Expanded Form

Compensation in Addition — Let's Practice!

Addition with Regrouping - Ten

Three Digit Addition with Regrouping - Expanded Form

Adding 2 Digit Numbers Using Standard Algorithm

Adding 3 Digit Numbers Using Standard Algorithm
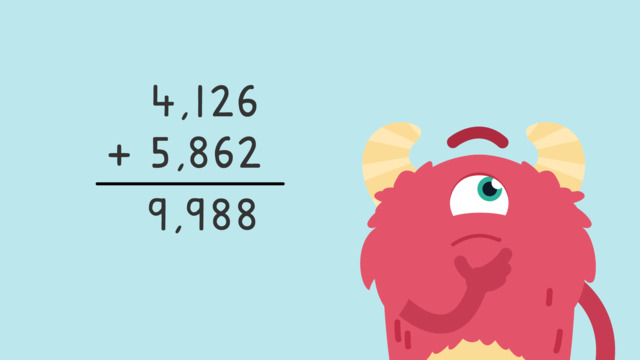
Adding Larger Numbers — Let's Practice!
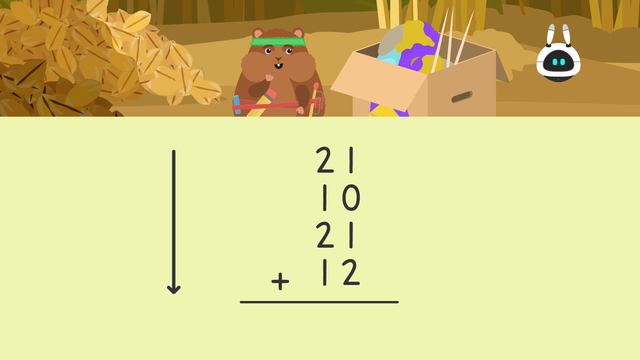
Adding Four Two Digit Numbers












