Writing Equivalent Algebraic Expressions with Addition and Subtraction
- Writing Equivalent Algebraic Expressions with Addition and Subtraction – Definition
- Understanding Equivalent Algebraic Expressions – Explanation
- Like Terms

Basics on the topic Writing Equivalent Algebraic Expressions with Addition and Subtraction
Writing Equivalent Algebraic Expressions with Addition and Subtraction – Definition
When we talk about algebra, we often find different expressions that can represent the same value or idea. This concept is crucial not just in mathematics but in solving problems in everyday life where flexibility and adaptation to various representations can lead to easier solutions. An equivalent algebraic expression is an expression that, although it may look different, has the same value as another expression when the variable(s) are substituted with the same number(s).
Equivalent algebraic expressions are different algebraic expressions that represent the same value.
Understanding Equivalent Algebraic Expressions – Explanation
To master the art of writing equivalent expressions, a fundamental skill in algebra, it's essential to understand not just the process of adding and subtracting expressions effectively, but also to deeply comprehend the components that make up algebraic terms and expressions. This comprehension includes recognizing and distinguishing between variables, constants, and coefficients, in addition to identifying like terms. Engaging with writing numerical expressions can significantly enhance your ability to manipulate and understand these algebraic concepts.
| Word | Definition | Example |
|---|---|---|
| Variable | A symbol representing unknown values that can change. | In $2x + 3$, $x$ is the variable. |
| Constant | A fixed value that does not change. | In $2x + 3$, $3$ is the constant. |
| Coefficient | A numerical factor that multiplies a variable in an algebraic expression. | In $2x + 3$, $2$ is the coefficient of $x$. |
| Term | A single mathematical expression consisting of a constant, variable, or both, possibly multiplied together. | $2x$ and $3$ are both terms in the expression $2x + 3$. |
Like Terms
Like terms are terms in an algebraic expression that have the same variable raised to the same power. The process of simplifying an expression by adding or subtracting like terms is known as combining like terms. This is a foundational skill for working with algebraic expressions.
Adding and Subtracting Algebraic Expressions
Adding or subtracting algebraic expressions involves combining like terms by adding or subtracting their coefficients. This method is straightforward yet powerful, allowing us to simplify complex expressions into more manageable forms.
Simplify $4x + x$
- Identify like terms: In the expression $4x + x$, both terms are like terms because they contain the same variable, $x$.
- Add the coefficients of like terms: The coefficient of $x$ in the term $x$ is $1$ (since $x$ is the same as $1x$). Therefore, when adding $4x$ and $x$, you are essentially adding $4x + 1x$.
- Perform the addition: Add the coefficients $4$ and $1$ to get $5$.
- Write the simplified expression: After adding the coefficients, the simplified expression is $5x$.
Simplify $7n + 3m - 5n + m$
- Identify like terms: In the expression $7n + 3m - 5n + m$, $7n$ and $-5n$ are like terms because they both contain the variable $n$. Similarly, $3m$ and $m$ are like terms because they both contain the variable $m$.
- Add the coefficients of like terms: The coefficients of $n$ terms are $7$ and $-5$, and for $m$ terms are $3$ and $1$ (since $m$ is the same as $1m$).
- Perform the addition: Add the coefficients of $n$ terms $7$ and $-5$ to get $2$, and add the coefficients of $m$ terms $3$ and $1$ to get $4$.
- Write the simplified expression: After adding the coefficients, the simplified expression is $2n + 4m$.
Simplify $-6w + w - k + 2k$
- Identify like terms: In the expression $-6w + w - k + 2k$, $-6w$ and $w$ are like terms because they both contain the variable $w$. Similarly, $-k$ and $2k$ are like terms because they both contain the variable $k$.
- Add the coefficients of like terms: The coefficients for $w$ terms are $-6$ and $1$ (since $w$ is the same as $1w$), and for $k$ terms are $-1$ (since $k$ is the same as $-1k$) and $2$.
- Perform the addition: Add the coefficients of $w$ terms $-6$ and $1$ to get $-5$, and add the coefficients of $k$ terms $-1$ and $2$ to get $1$.
- Write the simplified expression: After adding the coefficients, the simplified expression is $-5w + k$.
Practice combining like terms on your own now.
Writing Equivalent Algebraic Expressions – Application
Example 1: Imagine participating in a month-long fitness challenge. In the first week, you plan to complete $x$ minutes of cardio and double that amount in strength training. In the second week, you aim to increase your cardio by $30$ minutes while keeping strength training constant. How can you express the total minutes spent on each activity over the two weeks?
Expression:
First week cardio: $x$ minutes.
First week strength training: $2x$ minutes.
Second week cardio: $x + 30$ minutes.
Total minutes on cardio over two weeks: $x + (x + 30)$.
Total minutes of strength training over two weeks: $2x$ (no change in the second week).
Combining Like Terms:
Total cardio minutes: $2x + 30$.
Total strength training minutes: $2x$.
Example 2: You're working on an art project that requires blue and yellow paint. On the first day, you use $b$ ounces of blue paint and $y$ ounces of yellow paint. The next day, inspired, you decide to double your usage of blue paint but use half the amount of yellow paint. How can you express the total paint used?
Expression:
First day blue paint: $b$ ounces.
Second day blue paint: $2b$ ounces.
Total blue paint used: $b + 2b$.
First day yellow paint: $y$ ounces.
Second day yellow paint: $\frac{y}{2}$ ounces.
Total yellow paint used: $y + \frac{y}{2}$.
Combining Like Terms:
Total blue paint: $3b$ ounces.
Total yellow paint: $\frac{3y}{2}$ ounces.
Example 3: Your book club decides to read $n$ pages of a novel each week. However, during the second week, the club agrees to read an additional $10$ pages to finish earlier. How can you express the total pages read after two weeks?
Expression:
Week 1 pages: $n$.
Week 2 pages (with additional): $n + 10$.
Combining Like Terms:
- Total pages read after two weeks: $2n + 10$.
Try some on your own!
Writing Equivalent Algebraic Expressions with Addition and Subtraction – Summary
Key Learnings from this Text:
Equivalent algebraic expressions show the same value, useful in algebra and daily problem-solving.
Like terms share the same variable and power, vital for the simplification process.
A coefficient is a number multiplying a variable; a constant lacks a variable.
Simplifying expressions by adding/subtracting like terms aids in managing complex algebra problems.
Writing Equivalent Algebraic Expressions with Addition and Subtraction – Frequently Asked Questions
Transcript Writing Equivalent Algebraic Expressions with Addition and Subtraction
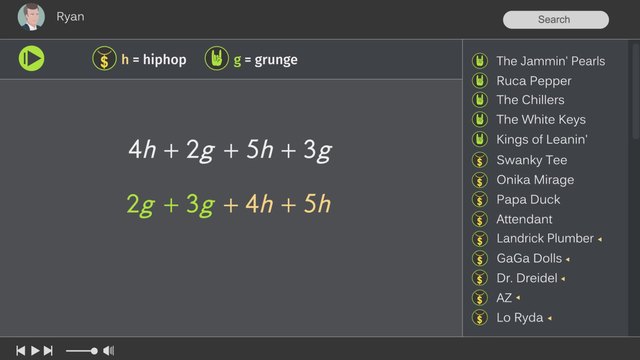
At the Top 40 Commutative Retirement Center, Ryan Secrets gets ready to host his annual New Year's Eve party. He's determined to make the party a big success because last year, he made a big mistake. He asked the guests to bring their own music and then he let them play whatever song they wanted in no particular order. As you can imagine, it was complete chaos! But, this year, Ryan has a plan to make a playlist by grouping the songs by genre. Let's help Ryan organize his playlist by writing equivalent algebraic expressions with addition and subtraction. Let's say you have a party and a friend brings four hip-hop songs and two grunge songs. Using ‘h’ to represent the hip-hop songs and ‘g’ to represent the grunge songs you can describe this situation with the algebraic expression, '4h plus 2g'. Now, imagine another friend brings 5 hip-hop songs and 3 grunge songs. You can write this as '5h + 3g'. Now, how many songs of each genre do you have? To write an equivalent expression, first, let's use the Commutative Property of Addition so that terms with the same variable are written together... These are called like-terms. Like-terms are terms in an algebraic expression that have the same variable raised to the same power. That means we combine the g’s and then the h’s by adding their coefficients, giving us '5g plus 9h'. Remember, coefficients are the numbers in front of the variables.
Okay, it's time to get this year’s party started! Three retirees just came in like a wrecking ball and each one brought music. What kind of music did they bring? They brought electronic dance pop and rock ballads. One of them brought 3 pop songs and 4 rock ballads another brought 2 electronic dance and 5 pop songs. And the last brought 4 electronic dance songs. Ryan Secrets removes three 3 rock ballads 2 pop .and 3 electronic dance songs because these songs are so five minutes ago. Let's help Ryan write an equivalent expression for this situation. First, use the Commutative Property to reorder the terms in alphabetical order then, just like we did before, we combine the like terms. Now, Ryan Secrets has some great playlists. This music is H...O...T -- HOT! So remember, when writing equivalent algebraic expressions use the Commutative Property of Addition to reorder the terms then combine like-terms. To help you remember this know that the word ‘commutative’ comes from the word ‘commute’, which means to go back and forth or move around. Ryan Secrets' system to reorder the playlist worked. This year's bash is a big success. Oh! It’s just after six in the evening; the party must be in full swing by now. Hmmm...what a shame...I guess no one's ringing in the new year!
Writing Equivalent Algebraic Expressions with Addition and Subtraction exercise
-
Write Equivalent Algebraic Expressions with Addition.
HintsIn order to simplify expressions, you can combine terms that have the same variable.
Coefficients are the numbers that come in front of the variable.
SolutionWhen writing algebraic expressions, your goal is to write the expression in the simplest form by combining like terms.
You can rearrange terms in an expression to group the like terms using the commutative property. Remember, the term "commute" means "to move." Therefore, the commutative property of addition allows you to reorder or move the terms around without changing the value of the expression.
Combining like terms means to add the coefficients, or the numbers in front of the variables, of the terms with the same variable together. Since the expression has two terms with $g$ and two terms with $h$, you can add the terms in each of these sets together. $2g+3g$ results in $5g$. $4h+5h$ results in $9h$.
Since $g$ represents grunge songs and $h$ represents hip-hop songs, there are a total of $5$ grunge songs and $9$ hip-hop songs on the playlist.
-
Simplify Algebraic Expressions with Addition and Subtraction.
HintsRemoving a song means that the coefficient should be negative.
When combining like terms, add the terms that have positive coefficients and subtract the terms that have negative coefficients.
SolutionWhen you subtract one term from another, this is equivalent to adding the opposite, or inverse, of that term. For example, if you want to subtract $4d$ from $7d$, this can be written as $7d+(-4d)$.
In the example, since you are removing $3$ rock ballads, $2$ pop songs, and $3$ electronic dance songs, you can express this by adding the inverses of each of these values; $-3r$, $-2p$, and $-3d$, respectively. This produces the expression $3p+4r+2d+5p+4d+(-3r)+(-2p)+(-3d)$.
Since you need to reorder the terms alphabetically to combine like terms, the expression is now written as $2d+4d+(-3d)+3p+5p+(-2p)+4r+(-3r)$.
Combining like terms results in the expression $3d+6p+1r$. Since the coefficient of $r$ is $1$, this could also be written as $3d+6p+r$.
Interpreting the coefficients and the variables, the playlist is left with $3$ electronic dance songs, $6$ pop songs, and $1$ rock ballad.
-
Write Algebraic Expressions from Real-world Scenarios.
HintsUse the given variables to write an expression to represent each sentence.
Determine whether you are adding or subtracting the terms in the algebraic expression.
Solution- In the first scenario, since the drama club is eating the bags of snacks that she brought to share, you need take the number of bags of each snack she brought, $10c+7p$ and subtract the number of bags eaten, $4c+6p$. This results in:
- In the second scenario, since you are trying to figure out how much both Lorenzo and Maya spend together, you will need to add the two expressions together. Lorenzo spends $12+3m$ dollars, and Maya spends $4+6m$ dollars. This results in:
- In the last scenario, since Michael is looking for a total of the number of each genre of books he read, you will need to add all of the expressions that represent books read each month together. This results in:
-
Match expressions with their equivalent forms.
HintsReorder the terms so they are in alphabetical order.
Pay careful attention to the signs before each term, as this tells you to add or subtract.
SolutionWhether you are simplifying expressions with integer or fractional coefficients, it is important to reorder the terms in alphabetical order first before you start adding or subtracting.
- For the first expression, you can reorder the terms to get $5x+(-2x)+3y+6y$. Remember, adding a negative number is equivalent to subtracting that number, so you can also express this as $5x-2x+3y+6y$. Combining the like terms results in an expression of $3x+9y$.
- The second expression already includes the operation of subtraction. When you reorder the terms, it is important to take the operation with the term it precedes. This results in the expression $9x+2x-4x-6y+3y-6y$. When combining the like terms, note that the first $y$ term is $-6y$. Adding $-6y+3y$ results in $-3y$, which in turn means that $-6y+3y-6y$ is $-9y$. Therefore, the correct simplified expression is $7x-9y$.
- In the third expression, although it contains fractions, you can still treat this like any other integer-only expression. Reordering the terms results in $5w-3w+\frac{1}{2}x+\frac{5}{2}x+3y-2y$. Combining like terms and adding the fractions, which already have a common denominator, produces the expression $2w+3x+y$.
- In the last expression, although not all fractions have the same denominator, you can reorder the terms so that all terms that have the same variable and a common denominator are together as well. For example, you can write this expression as $3w-2x+6x+\frac{3}{4}y-\frac{1}{4}y+\frac{1}{2}y$. Since $\frac{3}{4}y-\frac{1}{4}y+\frac{1}{2}y=\frac{2}{4}y+\frac{1}{2}y$, and $\frac{2}{4}y$ reduces to $\frac{1}{2}y$, the $y$ terms simplify to $\frac{1}{2}y+\frac{1}{2}y$, or $\frac{2}{2}y$, which is just $y$. Therefore, this entire expression is equivalent to $3w+4x+y$.
-
Create Algebraic Expressions from Scenarios.
HintsDo not combine two terms unless they are like terms.
A one time fee or cost does not need a variable.
If there are two separate items, there should be two variables.
SolutionIn the taxi ride scenario, every mile costs $\$ 2$. This cost can be represented by $\$ 2x$, where $x$ represents the number of miles. Since you would have to pay $\$ 3$ regardless of how long the taxi ride is, this is a constant value and does not need to be associated with a variable. Therefore, this entire cost can be represented by $2x + 3$ dollars.
For the scenario with Dominic, since he is buying two separate kinds of tickets, each type of ticket should be represented by a different variable. You can let $x$ represent the cost of a baseball ticket and $y$ represent the cost of a football ticket. Because he buys $3$ baseball tickets and $2$ football tickets, the total cost can be written as $3x+ 2y $ dollars.
For the fair scenario, admission to the fair is a one-time fee of $\$ 5$, so you do not need to associate this cost with a variable. Each ride, however, costs $2$ dollars. If you let $x$ represent the number of rides ridden, then the cost of the entire time at the fair can be written as $2x+ 5$ dollars.
For the scenario with Alexandra, she is purchasing two separate kinds of snacks: nachos and popcorn. You can let $x$ represent the cost of an order of nachos and $y$ represent the cost of a bag of popcorn. Therefore, the total cost of all of her snacks is $ 4x+ 3y$.
Because none of these expressions have like terms, they cannot be simplified any further.
-
Identify the correct expressions.
HintsA variable with no coefficient has a coefficient of $1$.
Equivalent expressions can be rewritten in any order, so long as the coefficient stays attached to its respective variable.
SolutionWhen simplifying expressions, there may be several ways to express equivalent expressions, so long as you are combining like terms properly.
In the first situation, Gabby wrote the expression correctly because she properly subtracted $8x-2x$ to get $6x$.Therefore, $8x+7y-2x+2y$ is equivalent to $6x+9y$. While John added the $y$ terms properly, he thought that the $x$ disappeared when he subtracted $8x-2x$.
In the second situation, Jamal wrote the expression correctly because he kept the coefficients attached to their corresponding variables when he reordered the terms. $7x+1$ is the same as $1+7x$. Jessica, however, reversed the coefficients of the two terms when she reordered the expression. $7x+1$ is not equivalent to $1x+7$.
In the last situation, Isaac simplified the two terms correctly because he added the coefficients of the two $y$ terms. Since $y$ can also be written as $1y$, $y+y$ is equivalent to $1y+1y$, which is equivalent to $2y$. Taylor added the exponents of the two $y$ terms instead.