Writing Products as Sums and Sums as Products

Basics on the topic Writing Products as Sums and Sums as Products
To express a product as a sum, apply the distributive property of multiplication over addition. And the other way around, to express a sum as a product, apply factoring. The ability to rewrite an expression in a different form allows flexibility and opens the mind to various possibilities in solving a mathematical problem. Learn how to express products as sums and sums as products by helping superhero En Fuego prepare a training regimen that would allow her to match the skills of her arch-rival superhero Ice Queen, the reigning champion, in a duel for this year’s upcoming Superhero supremacy showdown. Common Core Reference: CCSS.MATH.CONTENT.7.EE.A.1
Transcript Writing Products as Sums and Sums as Products
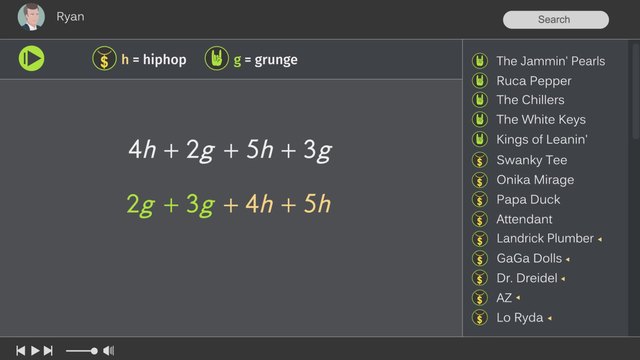
Two superheroes, En Fuego and the Ice Queen are lifelong rivals and are locked in a neverending duel for superhero supremacy. The last time they locked horns, the Ice Queen won. En Fuego, has been training hard to get even and win this year’s upcoming showdown. En Fuego can analyze the Ice Queen's abilities and create her own training regimen by expressing products as sums in differing ways. Let's give En Fuego a copy of the Ice Queen’s training routine so she can calculate the current abilities of the Ice Queen. Last year, the Ice Queen was able to change the temperature of objects by 32 degrees per second and create 2 ice spikes per showdown. Therefore, we can write 32x where 'x' represents seconds and then add 2 to represent the two icicles. This year, the Ice Queen’s training regimen allowed her to improve by a factor of 4. This means that we should multiply the Ice Queen's performance last year by 4. We can distribute the 4 over the parentheses, giving us 4 times 32x plus 4 times 2. Next, we can multiply and combine any like terms to get our final expression of the Ice Queen's updated powers. Last year, En Fuego was only able to change the temperature by 16° per second and produce one fireball per showdown. We can write the expression for En Fuego's powers like this: 16x represents by how much En Fuego can change the temperature per second and since she was able to produce one fireball per showdown, we'll add one. This year, En Fuego would like to at LEAST be as good as the Ice Queen. But how will En Fuego know how much to train? En Fuego wants to be able to change the temperature by 128 degrees per second and produce 8 fireballs...just like the Ice Queen. For En Fuego, we can write 128x to represent the change in temperature by 128 degrees per second plus 8 to represent the fireballs. En Fuego knows she has to increase her powers by more than a factor of 4, so she makes a little table to track her progress. As we said before, last year's performance can be described by 16x plus 1. Since En Fuego has to better her performance by at least a factor of 4, we'll start there. By increasing her performance by a factor of 4, En Fuego would be able to change the temperature by 64° per second and produce 4 fireballs per showdown. This isn't good enough. What if she increased her performance by a factor of 6? Now she's able to change the temperature by 96° per second and produce 6 fireballs! En Fuego is not quite satisfied with this. She at LEAST has to get even with the Ice Queen. Let's try increasing En Fuego's performance by a factor of 8 and see what happens. Bingo! If En Fuego can perform 8 times better than she did last year, she'll have a fighting chance against her rival: the Ice Queen. As we've just seen, there might be different ways to express products and sums. Let's take the expression 128x plus 8 and divide it up in a few different ways. Since both 128 and 8 are even numbers, we can also write this expression by taking out a 2 from each of the terms. If we do this, we get something that looks like this: This is read as: two times the quantity 64x plus 4. Alternatively, since both 128 and 8 are divisible by 4, we can do the same thing as before, but just divide by 4 instead of 2. Hey! This looks familiar! It's the expression of the Ice Queen's abilities from last year multiplied by a factor of 4. We can also divide 128 and 8 by 8, which would look like this: Hey! This looks familiar as well! It's the expression of En Fuego's abilities from last year multiplied by a factor of 8. As you can see, there are several different ways to write products as sums or sums as products. With both of the superheroes done with their respective training regimens. They face off once again in this year's competition. Looks like they’ll need to swim their way outta here.
Writing Products as Sums and Sums as Products exercise
-
Explain how to express the product $4(32x+2)$ as a sum.
HintsHere you see the distributive property.
Take care of the notation
- $a+b$ is a sum.
- $a\times b$ is a product.
Just look at the following example that looks quite similar:
$5(4x+2)=(5)(4x)+(5)(2)=20x+10$.
SolutionThe last year results of Ice Queen can be expressed by the term $32x+2$, where $x$ is the number of seconds.
With rigorous training, the Ice Queen improved last year's results by a factor $4$. So we have to multiply the sum above by $4$ to get $4(32x+2)$.
Next we use the distributive property to get $4(32x+2)=(4)(32x)+(4)(2)$.
Last, we combine like terms: $4(32x+2)=128x+8$.
-
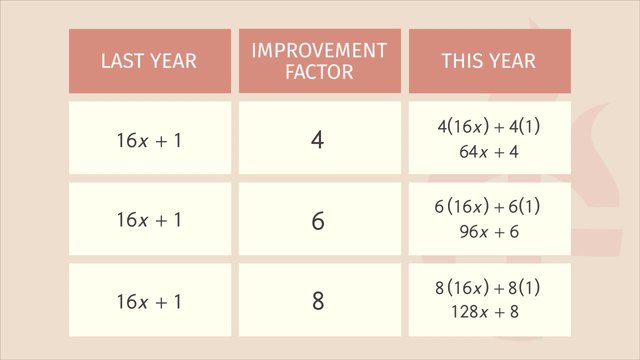
Determine how the different factors alter the expression $16x+1$.
HintsUse the distributive property, $a(b+c)=(a)(b)+(a)(c)$.
For example, $4(16x+1)=(4)(16x)+(4)(1)$.
SolutionHere you see the complete table.
Let's fill it in step by step.
In the left column, you see last year's results of En Fuego.
In the middle column, the improvement factor is written down.
You have to multiply last year's results with this factor each time to get the improvement results for this year:
- $4(16x+1)=(4)(16x)+(4)(1)=64x+4$
- $6(16x+1)=(6)(16x)+(6)(1)=96x+6$
- $8(16x+1)=(8)(16x)+(8)(1)=128x+8$
-
Explain how to express the sum $120x+16$ as a product.
HintsYou can also factor out $8$:
- $\frac{120x+16}8=15x+2$
- $120x+16=8(15x+2)$
You can check the resulting product using the distributive property.
SolutionTo write this sum as a product we first look for all factors of the first as well as the second summand.
- $120x=(2)(2)(2)(3)(5)(x)$
- $16=(2)(2)(2)(2)(2)$
Let's start with the factor $2$:
For this we divide the whole sum by $2$: $\frac{120x+16}2=60x+8$.
The other way round we can write the common factor in front of a set of parentheses $2(~~~)$. Inside the parentheses we write the sum $60x+8$ to get in total
$120x+16=2(60x+8)$.
Similarly we can factor out $4$:
- $\frac{120x+16}4=30x+4$
- $4(~~~)$ and last we put the sum $30x+4$ inside the parentheses.
Once again we factor out $8$.
- $\frac{120x+16}8=15x+2$
- $8(~~~)$ and last we put the sum $15x+2$ inside the parentheses.
Last we can state that each product is correct. Usually one factors out the greatest common factor. Here it's $8$.
-
Write each sum as a product.
HintsYou can check each product using the distributive property.
Keep in mind, that you can factor out any factor in common.
For example, $24x+16=2(12x+8)=4(6x+4)=8(3x+2)$.
SolutionTo write a sum as a product, we have to find factors in common for both summands.
The other way round we can check the product using the distributive property. So we can state that factoring and using the distributive property are opposite operations.
Let's start with the sum $125x+15$.
- $125x=(5)(5)(5)(x)$
- $15=(3)(5)$
$~$
The next sum is $132x+33$.
- $132x=(2)(2)(3)(11)(x)$
- $33=(3)(11)$
$~$
The next sum is given by $120x+30$.
- $120x=(2)(2)(2)(3)(5)(x)$
- $30=(2)(3)(5)$
$~$
There is just one sum left: $136x+8$.
- $136x=(2)(2)(2)(17)(x)$
- $8=(2)(2)(2)$
-
State how to express the product $4(16x+1)$ as a sum.
HintsIf you multiply a factor by a sum, you use the distributive property, $a(b+c)=(a)(b)+(a)(c)$.
Combining like terms means, for example, $(5)(2)(y)=10y$.
Here the numbers $5$ as well as $2$ have been multiplied to $10$.
The result on the right side should be a sum.
SolutionFirst, we multiply the factor by each sum in the parentheses:
- $(4)(16x)$
- $(4)(1)$
- $(4)(6x)=64x$
- $(4)(1)=4$
-
Represent products as sums and vice versa.
HintsThere is one calculation without any mistake.
To write a product as a sum use the distributive property.
Just look at the example beside.
To write a sum as a product look for the common factors of all given terms. For example,
- $24x=(12)(2x)$
- $12y=(12)(y)$
- $36=(3)(12)$
Next divide each term by the common factor.
You can check your factorization by using the distributive property.
SolutionKeep the following in mind:
- To write a product as a sum use the distributive property.
- The other way round, to write a sum as a product look for common factors of all given terms.
$~$
$\mathbf{124x+24}$
- $124x=(2)(2)(31)(x)$
- $24=(2)(2)(2)(2)(3)$
- $124x\div 4=31x$
- $24\div 4=6$
$~$
$\mathbf{4(13x+5)}$
Here we have to use the distributive property: we multiply each term in the sum by $4$ and combine the like terms:
$4(13x+5)=(4)(13x)+(4)(5)=52x+20$.
$~$
$\mathbf{24x+12y-36}$
The common factor here is $12$. Dividing each term by $12$ leads to
- $24x\div 12=2x$
- $12y\div 12=y$
- $36\div 12=3$
$~$
$\mathbf{24(x+2y-6)}$
Again we use the distributive property
$24(x+2y-6)=(24)(x)+(24)(2y)-(24)6$
and combine the like terms
$24(x+2y-6)=24x+48y-144$.