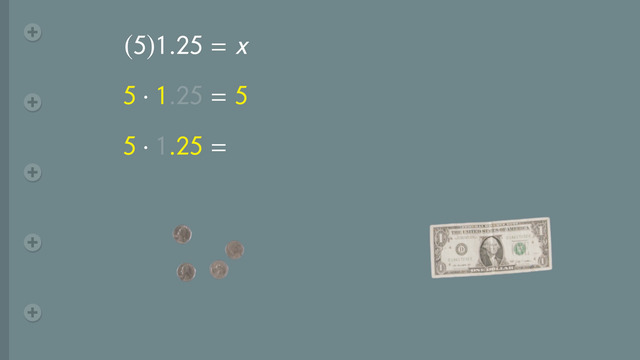What Makes a Number Sentence True or False?


Basics on the topic What Makes a Number Sentence True or False?
Constructing a number sentence from a real world situation is a critical step in using mathematics in everyday life. Checking the validity of a number sentence, which can either be an equation or an inequality, is an important skill to develop. The proper recognition and understanding of the relationship that exists among the components of a number sentence is the key in developing and strengthening one’s problem-solving and analytical skills. Learn what makes a number sentence true or false by helping Zippy find his dog, Strumpy, who ran into an old abandoned amusement park as he figures out the truth of the number sentences written on the electrical box and the ferris wheel’s control panel. Common Core Reference: CCSS.MATH.CONTENT.6.EE.B.5
Transcript What Makes a Number Sentence True or False?
Late one night, Zippy and his dog Strumpy are out for a walk when all of a sudden, Strumpy catches a scent and takes off! It looks like he ran into the old, abandoned amusement park. Hey...those look like...paw prints in the mud! But it's getting dark...so, it's hard to tell. If only there was a way to turn these lights on. That's when Zippy sees an electrical box. But there are some strange numbers and symbols written on it. It looks like in order to find his dog and solve this mystery. Zippy is going to need to figure out what makes a number sentence true or false. Take a look at the three number sentences written on the electrical box… Do you see anything strange about them? Some of these number sentences are definitely not true. But which ones? The first number sentence reads "4 + 6 is less than 9".
But 4 + 6 is equal to 10, and 10 is greater than 9, so this number sentence is definitely false. Next: 3 times 6 is equal to 18. This number sentence is true because the expressions on both sides of the equal sign are equal to 18. Finally, 22 is greater than or equal to 11 plus 12.
Well, 11 plus 12 is equal to 23, so this last number sentence is false. But how does this help Zippy find Strumpy? Zippy flips the inequality symbols to make all three number sentences true and look there, the lights turned on! But wait a second. What’s that noise? That’s definitely not Strumpy! Let's get out of here! Back at the entrance he hears a bark coming from the direction of the Ferris Wheel. How did Strumpy get up there? Let´s get him down! Zippy finds the ferris wheel's control panel and, just like the electrical box, there are three number sentences written on it but these number sentences have variables. How can he figure out which ones are true and false if he doesn't have a number to substitute in for 'x'? Zippy finds a weird punch card with the number 10 written on it just lying next to the control panel. Maybe this will help him find Strumpy? Maybe if we substitute 10 in for 'x', we can make one of these number sentences true! Let's try it out. If we substitute 10 in for 'x' in the first sentence we get 25 minus 10 is less than 15. Since 15 is not less than 15, this number sentence is false. If we substitute 10 in the next sentence. We get 13 is greater than or equal to 10 plus 4, or 14.
13 is not greater than or equal to 14, so this is false too. Last chance 70 divided by 10 is equal to 7. Yes! That's a true number sentence! Zippy inserts the number 10 card and is about to turn on the Ferris Wheel but wait a minute it looks like somebody wants to help... Oh. Well that was nice of him. Maybe that swamp monster isn’t so bad after all maybe the whole time, he just wanted to be swamp friends.
What Makes a Number Sentence True or False? exercise
-
Identify the false number sentences.
HintsFirst, simplify the given expressions.
Next, decide if the relation becomes true.
Just look at the following examples:
- $13>12$
- $13\ge12$
- $13=13$
There is only one true sentence.
SolutionPoor Ziggy. He lost his dog. Unfortunately, he has to solve different problems to turn the lights on so that he can see where his dog has gone:
- $4+6<9$? Is this true or false? First, we do addition on the left side of the relation sign: $4+6=10$. Sure, $10$ is not smaller than $9$ and thus this sentence is false.
- $3\times 6=18$? What about this sentence? Again we calculate the product $3\times 6$. The result is $18$. Thus this sentence is true.
- $22\ge 11+12$? Again we do addition first $11+12=23$. But $22$ isn't greater or equal to $23$. So this sentence is false too.
-
Analyze the number sentences.
HintsFirst, put $x=10$ into the sentence. For example, $10+x$ leads to $10+10=20$.
Next, decide if the relation is true or false. For this, remember
- $20>15$
- $20\ge 20$
- $20=20$
Pay attention: $20\ge 20$, but $20\not > 20$.
SolutionZiggy has to put $x=10$ in for each sentence to check the sentences.
$\mathbf{25-x<15}$ leads to $25-10=15<15$? This is false because $15=15$ but not less than $15$.
$\mathbf{13\ge x+4}$ leads to $13\ge 10+4=14$? But $13<14$ and so this sentence is false too.
$\mathbf{\frac{70}x=7}$ leads to $\frac{70}{10}=7$? Sure, this is true.
-
Determine which numbers make the number sentences true.
HintsPut each value for $x$ in the equation first. Check the inequality after.
Five values for $x$ which satisfy the inequality.
There is only one value for $x$ which fulfills neither the equation nor the inequality.
SolutionNot again, Ziggy thinks. He has to solve another problem to get a coke and a taco for relaxation time.
Let's start with the equation: $3\times x=15$. We check it with each given value for $x$.
- $x=1$ $\rightarrow$ $3\times 1=3\not = 15$
- $x=2$ $\rightarrow$ $3\times 2=6\not = 15$
- $x=3$ $\rightarrow$ $3\times 3=9\not = 15$
- $x=4$ $\rightarrow$ $3\times 4=12\not = 15$
- $x=5$ $\rightarrow$ $3\times 5=15$ ✓
- $x=6$ $\rightarrow$ $3\times 6=18\not = 15$
Enjoy your relaxation time with your dogs, Ziggy.
-
Find the mistakes.
HintsFirst, calculate the given terms. For example $3\times 7=21$.
Differentiate between $<$ and $\le$. Just look at the following example:
- $12\le 12$ but
- $12\not < 12$.
$\le$ includes $=$. In the same way $\ge$ includes $=$.
SolutionThe dogs are sleeping and Ziggy is still a little jumpy. What's the best you can do when you're jumpy: check relation sentences of course! So this is what Ziggy does.
- $3+7\le10$? First, he does the addition on the left side $3+7=10$. This sentence is true because $\le$ includes $=$.
- $3+7<10$ looks quite familiar. What's the difference? Here we have the $<$ sign and, sure, $10$ is not less than $10$. Thus this sentence is false.
- $x+7\le 10$. Here we have a variable $x$ for which we put $2$ in to get $2+7=9\le10$. This is a true sentence.
- $3\times 7>10$. Again we do the math first, i.e. $3\times 7=21$. $21>10$? Absolutely, this is a true sentence.
- $3\times 7-11>10$. This looks a little bit more complicated. First, we determine the left side to get: $3\times 7-11=21-11=10$. But $10$ isn't greater than $10$ itself. This sentence is false.
- $7-3\ge 5$? The difference is $7-3=4$ and $4$ is less than $5$. This sentence is false too.
-
Categorize the different kinds of number sentences.
HintsLook at the relation sign in the given sentence.
You have to assign two sentences to each relation sign.
$<$ means "less than" and $>$ means "greater than".
Just read the sentences from left to the right and not the other way round.
SolutionIn each of the following sentences the relation sign is highlighted, so you can recognize it directly:
- $4+6 \mathbf{\color{#669900}{<}} 9$
- $25-x \mathbf{\color{#669900}{<}} 15$
- $22 \mathbf{\color{#669900}{>}} 11+12$
- $13 \mathbf{\color{#669900}{>}} x+4$
- $3\times 6 \mathbf{\color{#669900}{=}} 18$
- $70\div x\mathbf{\color{#669900}{=}} 7$
-
Determine the relation sign to make the number sentence true.
HintsThe relation sign isn't unique. You can use different ones to make the sentence true.
Just look at the following example:
$3$ ___ $4$.
Here you can put in $<$ as well as $\le$ in place of the ___ to make this sentence true.
Simplify the terms as much as possible first.
SolutionFirst, we have $3\times (5+4)$ ___ $30-6$:
Simplify the given expression using PEMDAS:
- $3\times (5+4)=3\times )=27$
- $30-6=24$
Next, we have $3\times 5+4$ ___ $60\div 2$:
- $3\times 5+4=15+4=19$
- $60\div 2=20$
Then we have $3\times 5-6$ ___ $27\div(2+1)$
- $3\times 5-6=15-6=9$
- $27\div(2+1)=27\div 3=9$
Finally, we have $3\times 5-6$ ___ $27\div(3\times 3)$:
- $3\times 5-6=15-6=9$
- $27\div(3\times 3)=27\div9=3$