Unknown Area Problems on the Coordinate Plane


Basics on the topic Unknown Area Problems on the Coordinate Plane
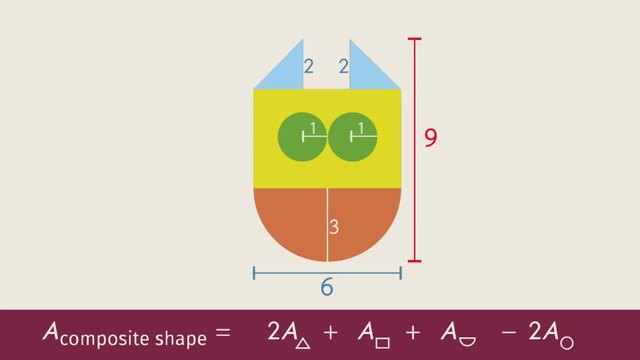
A composite shape is an irregularly-shaped figure that can be broken up into simpler, more basic shapes like rectangles, squares, triangles, trapezoids, circles, or even half circles. The area refers to the number of square units that can fit in the region bounded by the composite shape. To compute for its area on a coordinate plane, first, split up the composite shape into non-overlapping basic shapes and identify the x and y coordinates of all relevant vertices if the basic shape is a polygon or the endpoints of a diameter if the basic shape is a circle or a half circle. Then, find the area of each individual basic shape by evaluating the appropriate area formula and computing for the necessary dimensions based on the coordinates. Finally, compute for the area of the composite shape by combining the areas of the individual basic shapes and get the actual area of the foundation by multiplying the resulting area on the coordinate plane by the corresponding scale factor. Learn how to determine the area of composite shapes on a coordinate plane by helping Mr. Tad Dunlop, a real estate tycoon, and his construction site manager interpret the architect’s building plan for the foundations of two new skyscrapers in Grid City. Common Core Reference: CCSS.MATH.CONTENT.6.G.A.3
Transcript Unknown Area Problems on the Coordinate Plane
Welcome to Grid City. Mr. Tad Dunlop, a real estate tycoon, is working on a project to build two new skyscrapers. But just as they are about to lay the foundation, the construction site manager reports that they’ve miscalculated the amount of cement needed. So it looks like Mr. Dunlop and the site manager are going to have to go back to the architect's plans for the project. This way they can figure out the area of composite shapes on a coordinate plane. Let's apply a coordinate plane to the architect's plans. The shapes represent the foundations of the skyscrapers. Each of the boxes on the grid represents an area of 100 square meters, which will be the scale for our grid. For squares and rectangles, we can find the area by counting the number of squares inside the shape. But for all other shapes, we're going to have to find another way to calculate area. Let's take a look at the plan for building 1. To figure out how much concrete is needed, we could just count the number of square units inside. But this could take a long time, and we can't count the partial squares accurately. So to calculate the area, we can’t just count the squares inside the shape. But what we can do, is break it up into smaller shapes that are easier to work with. When we combine smaller shapes to make one larger shape, we call the larger shape a 'composite shape'. If we divide here and here, we can create a rectangle, a triangle, and a half-circle. Okay, now let’s calculate the area of these individual shapes. To find the area of the rectangle, we first need to know the side lengths. In order to find out how long the sides are, we first need to look at the coordinates that make up the rectangle. Notice how the y-coordinates are the same here and here, so to find the length of this side, we simply need to find the difference in the x-coordinates. 10 minus 2 is 8, so this side length is 8. We also need the height of the rectangle. Finding this is easy! We just have to subtract the y-coordinates. Hey! Would you look at that! Both of the sides are the same length, which makes this rectangle a square. So to find the area, we just take our 8 units and square it. That gives us 64 square units. Now for the area of the triangle. We already know the base is 8 units long because it's the same length as the square's side. The height can be found by finding the difference between the y-coordinates of this vertex and the base. Since the area of a triangle is one half the base times the height, we can just substitute our known values and calculate the area. That gives us a total of 20 square units. For our final piece, let’s calculate the area of the semicircle. The area of a circle is pi, 'r' squared. So a semicircle, or half a circle, is one-half times that. The radius is equal to 4 units. So we square that, then divide by half to get 8π. Using 3.14 for pi, we get about 25.12 square units. Now, to calculate the area of the whole composite shape, just add these three areas together. So, the composite area of the foundation of building 1 is approximately 109.12 square units. There is one more building in this development. We can see that it has four sides, but it’s not a square or a rectangle. Can you see any simple shapes in this composite shape? Look at that! That looks like a trapezoid, and a triangle. The formula for the area of a trapezoid is one-half times the sum of the two bases times the height. That formula looks weird, right? But let's look at the pieces of the formula. Look at that! One-half times the quantity base 1 plus base 2. That's the formula for the average length of the two bases! In order to find out how long the bases are, we first need to look at the coordinates that make up the trapezoid. Notice how the y-coordinates are equal. To find the length of base 1, we simply need to find the difference in the x-coordinates. To find the length of base 2, we just have to repeat the same process. We also need the height of the trapezoid. We can get the height of the trapezoid by subtracting the y-coordiates of our two bases. 10 - 6 is 4, so our height is 4 units. Now to do the math. We substitute our base lengths and height into the equation. As always, parentheses first, then multiplication, then multiplication one more time. The area of the trapezoid is 40 square units. Let's look at the triangle next. The base of the traingle is the same as base two of the trapezoid. The height is established by subtracting the y-values, 4 from 6. We can substitute our base and height values. So the area of the triangle is 8 square units. Now we just need to add the area of the trapezoid with the area of the triangle to find the total composite area. Remember, since each of our units is 100 square meters, we need to multiply both our final composite shapes by 100 to find the total area of the foundation of the buildings. By combining all the shapes we know the total area. That results in 15,712 square meters to cover in cement. Now Mr. Tad Dunlop and his site manager have enough information to order the cement and it looks like it's just arriving to the building site. Hey that's a nice statue, but I didn't see it in the building plans. We might have to take another look at those numbers.
Unknown Area Problems on the Coordinate Plane exercise
-
Explain how to calculate the area of a composite shape on a coordinate plane.
HintsYou can determine each needed length by subtracting coordinates of the given points.
For example, the radius of the circle is given by
$r=\frac{10-2}2$
Taking the formula for the area of a rectangle:
$A=lh$
If $h=12$ and $l=8$ we still have to plug in those values.
$A=(12)(8)=96$ units squared.
SolutionHere you see the separation of the given shape in (from top to the bottom) a semicircle, a rectangle, and a triangle.
So we need the corresponding formulas for the different shapes, as well as the values to plug in those formulas.
Let's start with the rectangle. First, we determine the length $l$ as well as the height $h$ using the coordinates of the given points
- $l=10-2=8$
- $h=13-5=8$
$A=s^2$
where $s$ is the length of the side of the square. Here $s=8$, which we plug in the formula to get
$A=(8)^2=64$ units squared.
Let's establish the area of the triangle using the formula
$A=\frac{1}{2}bh$
- $b=l=8$ the length of the rectangle.
- $h=5-0=5$
$A=\frac{1}{2}(8)(5)=20$ units squared.
There's just the semicircle left. For this, we need the following formula for area of a circle:
$A=\pi r^2$
and multiply it by $\frac{1}{2}$ because a semicircle is half of a circle. Then, we plug $r=4$
$A\approx\frac{1}{2}(3.14)(4^2)\approx(8)(3.14)\approx 25.12$ units squared.
Lastly, we have add all those results to get the total area:
$64+20+25.12=109.12$ units squared.
The wanted area is $109.12\cdot 100~m^2=10,912~m^2$.
-
Determine the area of the composite shape.
HintsBoth lengths $b_1$ as well as $b_2$ are given as the difference of the x-coordinates of the given points.
You could also count the units by the number of boxes.
The sum of $b_1$ and $b_2$ is $20$.
Notice there is a height of the trapezoid and a different height of the triangle.
SolutionThe given shape can be separated into one trapezoid and one triangle.
All of the needed lengths or heights can be determined as the difference of coordinates of the given points.
The formula for the area of a trapezoid is given by
$A=\frac12(b_1+b_2)h$
So, we need
- $b_1=0-(-12)=12$
- $b_2=-2-(-10)=8$
- $h=10-6=4$
$A=\frac12(12+8)(4)=40$ units squared.
For the triangle we need the formula
$A=\frac{1}{2}bh$
with
- $b=b_2=8$
- $h=6-4=2$
$A=\frac12(8)(2)=8$ units squared.
We still have to add those results to get the total area
$40+8=48$ units squared. Last we multiply this value with $100$ to get the $m^2$
$48\times 100=4800~m^2$
-
Determine the area of the new amusement park.
HintsYou can break this composite shape up into a semicircle, right triangle, and rectangle.
Recall that the area of a right triangle is half the area of a rectangle.
Use the following formulas:
- Circle: $A=\pi~r^2$
- Rectangle: $A=lh$
- Triangle: $A=\frac12bh$
SolutionIn the image you can see how we've broken up the composite shape to 3 shapes we already know.
- Area of the Semicircle
We plug the radius in the formula for a circle:
$A=\pi~r^2$
to get
$A_1=(3.14)(1.5)^2=7.065\approx 7.1$ square units.
- Area of the Rectangle
$l=10-4=6$
$h=4-1=3$
Now we plug those values in the formula for area of a rectangle:
$A=lh$
This gives us $A_2=(6)(3)=18$ square units.
- Area of the Right Triangle
Any side of the triangle can be a base. All that matters is that the base and the height must be perpendicular. The height is the line from the opposite vertex and perpendicular to the base.
$h=7-4=3$
$b=10-4=6$
Then we use the area of a triangle formula: $A=\frac12bh$
So we get $A_3=\frac12(6)(3)=\frac12(18)=9$ square units.
- Area of the Composite Shape
-
Find the errors in the calculations for the area of the composite shapes.
HintsYou can estimate the lengths as well as the areas using the coordinate plane.
Use the following formulas:
- Circle $A =\pi~r^2$
- Square $A =s^2$
- Trapezoid $A=\frac12(b_1+b_2)(h)$
- Triangle $A=\frac{1}{2}bh$
There are a total of five mistakes.
SolutionFor composite shapes we need a few formulas. The formulas we need for these figures above are:
- Circle $A=\pi~r^2$
- Square $A=s^2$
- Trapezoid $A=\frac12(b_1+b_2)(h)$
- Triangle $A=\frac{1}{2}bh$
$~$
Square and Semicircle
The needed lengths are
- $r=\frac{4-1}{2}=1.5$
- $s=4-1=3$
- Semicircle $A =\pi~(1.5)^2\approx7.1$ square units
- Square $A=3^2=9$ square units
$~$
Trapezoid and Triangle
The needed dimensions are for the trapezoid:
- $b_1=3-(-2)= 3 +2=5$
- $b_2=4-(-1)=4+1=5$
- $h=10-6=4$
- $b=5$
- $h=2$.
- Trapezoid $A=\frac12(5+5)(4)=(5)(4)=20$ square units
- Triangle $A=\frac12(5)(2)=\frac12(10)=5$ square units
$~$
Trapezoid and Semicircle
The needed values are
- $b_1=2-(-1)=3$
- $b_2=4-(-2)=6$
- $h=9-6=3$
$A_{\text{trapezoid}}=\frac12(3+6)(3)=(4.5)(3)=13.5$ square units.
The semicircle has the radius $r=\frac{b_2}2=3$ and thus we have
$A_{\text{half circle}}=\pi~(3)^2\approx28.26$ square units.
So, we still have to add those results. This gives us the total area of the composite shape
$A=13.5+28.26=41.76$ square units.
-
Find the formulas for the different shapes.
HintsTake the special triangle, a right triangle. This is the half of a rectangle. So the area is the half of the product of both legs.
A square is a special rectangle.
The area of a rectangle is given by the formula $A=lh$,
where $l$ is the length and $h$ the height.
SolutionTo determine areas of composite shapes you have to memorize several formulas for areas:
- A circle with the radius $r$ has the area $A=\pi r^2$ where $\pi\approx 3.14$.
- A square with the side length $s$ has the area $A=s^2$.
- A triangle with the base, $b$, and the corresponding height, $h$, has the area $A=\frac{1}{2}bh$.
- A trapezoid has two parallel sides with base lengths $b_1$ as well as $b_2$. The height of the trapezoid is $h$. So we use the following formula to determine the area $A=\frac{1}{2}(b_1+b_2)(h)$.
-
Determine how expensive the new school’s playground is going to be.
HintsThis composite shape is made up of a triangle and a trapezoid.
Use the following formulas:
- Triangle $A=\frac12(b)(h)$
- Trapezoid $A=\frac12(b_1+b_2)(h)$
$b_1$ and $b_2$ are the lengths of the parallel sides of the trapezoid.
For example $b_1=4-(-1)=4+1=5$.
The height of the trapezoid is $h=12-8=4$.
The side length of the triangle is $b=b_1=4-(-1)=4+1=5$ and the height is $h=8-5=3$.
Don't forget to include the correct units in your answer.
SolutionThis composite shape is made up of a trapezoid and a triangle
The needed lengths for the trapezoid are:
- $b_1=4-(-1)=5$
- $b_2=3-(-3)=6$
- $h=12-8=4$.
- $b=b_1=5$
- $h=8-5=3$.
- Trapezoid: $A=\frac12(5+6)(4)=(11)(2)=22$ square units
- Triangle: $A=\frac12(5)(3)=\frac12(15)=7.5$ square units
Each square unit corresponds to $100~ft^2$. This gives us the area
$A=29.5\times 100=2950~ft^2$. Since each square foot costs a dollar the resulting amount the class has to collect is $ \$ 2,950.00$.