Volume of Prisms

Basics on the topic Volume of Prisms
After this lesson, you will be able to find the volume of a prism using a general formula, and understand where it comes from.
The lesson begins by teaching you that the volume of a prism is equal to the product of its height and area of its base. It leads you to learn how to find the volume of a prism using a general formula. It concludes with a summary on how to find the volume of any prism.
Learn about the volume of prisms by helping Dr. Evil choose the right tank for his piranhas.
This video introduces new concepts, notation, and vocabulary such as a prism (a solid object with two identical ends and flat sides) and the volume of a prism.
Before watching this video, you should already be familiar with finding the areas of polygons, like rectangles, squares, and triangles.
After watching this video, you will be prepared to learn how to apply the general formula for the volume of a prism.
Common Core Standard(s) in focus: 7.G.B.4 and 7.G.B.6 A video intended for math students in the 7th grade Recommended for students who are 12-13 years old
Transcript Volume of Prisms
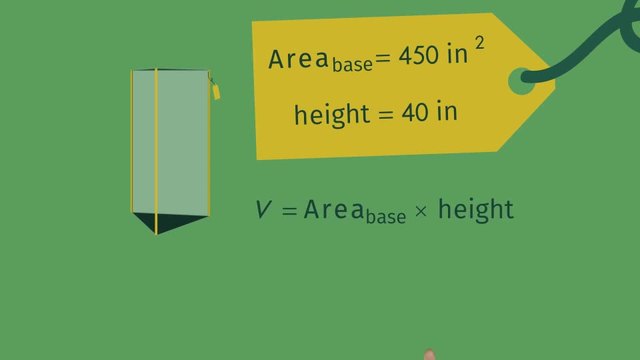
Call now to receive your shipment of premium, evil piranhas! But wait, if you order within the next 3 minutes, you'll receive the best discount ever! Don't miss this amazing deal-of-a-lifetime! Dr. Evil was so convinced by the infomercial that he absolutely had to add some piranhas to his evil caché of animals. The only problem is that he needs to purchase an evil fish tank before they are delivered, so he decides to check out the local, evil pet shop. But in order to figure out the correct size, he needs to calculate the Volume of Prisms. Since he ordered 8 piranhas and since each piranha needs at least 3,000 cubic inches of water to remain evil, he'll need a tank with a volume of at least 24,000 cubic inches to ensure that the piranhas have enough evil space to swim around evily. There are so many evil aquariums to choose from, but which is the most evil? First, he sees an aquarium that's a triangular prism, which is a prism with a triangle as its base. Unfortunately, the total volume isn't listed in the store. So, let's help Dr. Evil figure out the volume of the tanks. From the info tag, we can see that the triangular base has an area of 450 square inches and that the height of the tank is 40 inches. How can we use this information to help Dr. Evil calculate the volume of this tank? The volume of any prism is the area of its base times its height. By substituting in the values for the area of the base and the height, the volume of this triangular prism comes out to be 18,000 cubic inches. Unfortunately, that's too small for all the evil fish Dr. Evil wants. Besides, Dr. Evil doesn't want to be evil to his evil fish. Next, Dr. Evil takes a look at the classic evil aquarium, shaped like a rectangular prism. It's called a rectangular prism because the base of the tank is a rectangle. We can see that the info tag says that the width of the tank is 48 inches, the depth is 21 inches, and the height is 35 inches. In order to use the same formula – the volume of the prism equals the area of the base times the height – we need to help Dr. Evil figure out the area of the base. We just don't know the area of the rectangle yet, but if you remember, the formula for the area of a rectangle is simply the product of its two sides. In the case of this evil aquarium, the area of the base can be found by multiplying the width by the depth. This leaves us with the formula for the volume: width times depth times height. Substituting in the values gives us a volume of 35,280 cubic inches. Great! That's plenty evil enough! All of his new piranhas will have enough space for their evil fishy doings. Let's review. When calculating the volume of a prism, you just need to know two things: the area of the base and the height. Then, to get the volume, you simply multiply those two together. Be sure to check the units before you multiply! You don't want to multiply feet times meters! That would be evil! Additionally, the shape of the base doesn't matter, the formula always works. The volume of a prism equals the area of the base times the height, or 'v' equals 'b' times 'h'. Now, he's back at home and his evil fish tank is all set up. A delivery comes and he eeeeevily opens the box. Toy fish? That's not what he ordered... or is it? Remember, always be sure to read the EVIL fine print!
Volume of Prisms exercise
-
Identify the steps for calculating the volume of rectangular prisms.
HintsAll prisms have a 2-dimnesional shape on the bottom of the 3-dimensional figure. For example, a rectangular prism has a rectangular base.
The area of the base is calculated by the area formula for the given figure.
- For example, a rectangular prism has a rectangular base and the area of a rectangle is length $\cdot$ width, or $lw$, where $l$ represents length and $w$ represents width.
The volume of a rectangular prism with length $15~\text{in}$, width $8~\text{in}$, and height $17~\text{in}$, can be calculated by the formula,
- $V=15 ~\text{in} \cdot 8~\text{in}\cdot 17~\text{in}$
- Therefore, the volume is $2,040~\text{in}^3$.
SolutionVolume is the amount of 3-dimnesional space an object occupies.
When calculating the volume, you need to know two things:
1. The area of the base.
2. The height of the prism.
Then, to get the volume, we multiply them together.
- Volume $=$ area of the base $\cdot$ height
The base of a rectangular prism is a rectangle and the area of a rectangle is the product of the two sides.
- Area of Base $=$ length $\cdot$ width
- $V=$ length $\cdot$ width $\cdot$ height
- $V=lwh$
- $V=Bh$ where $B$ represents the area of the base.
The volume of a rectangular prism with length $47~\text{in}$, width $20~\text{in}$ and height $32~\text{in}$ can be calculated by the formula,
- $V=$ $47~\text{in}\cdot 20~\text{in}\cdot 32~\text{in}$
-
Sort the steps for calculating the volume of a triangular prism.
HintsRemember to always start with the needed formula. Here that is $V=Bh$ where $B$ is the area of the prism's base, and $h$ is the height of the prism.
Next, find the area of the base which is represented by $B$.
$B$ can vary depending on the type of prism.
- If the prism is rectangular, $B$ is the area of a rectangle, $lw$, where $l$ is the length of the rectangle and $w$ is the width of the rectangle.
A triangular prism with height $18~$in and a triangular base that measures $16~$in across its base, and $12~$in high, is calculated using the following steps:
1. $V=Bh$
2. $B=\frac{1}{2}16~\text {in}\cdot 12~\text {in}$
3 $B=96~\text{in}^2$
4. $V=96~\text{in}^2\cdot 18~\text{in}$
5. $V=1,728~\text{in}^3$
SolutionThe following steps are used to calculate a triangular prism with height $17~\text{in}$, and a triangular base that measures $10~\text{in}$ across its base and $5~\text{in}$ high.
1. $V=Bh$
2. $B=\frac{1}{2}\cdot10~\text{in}\cdot 5~\text{in}$
3. $B=25~\text{in}^2$
4. $V=25~\text{in}^2\cdot 17~\text{in}$
5. $V=425~\text{in}^3$
Important Side Notes:
1. $B$ represents the area of the base, and can vary depending on the type of prism.
- If the prism is rectangular, $B$ is the area of a rectangle, $lw$, where $l$ is the length of the rectangle and $w$ is the width of the rectangle.
- If the prism is traingular, $B$ is the area of a triangle, $\frac{1}{2}bh$, where $b$ is the base of the triangle and $h$ is the height of the triangle.
- The height of the triangular base.
- The height of the triangular prism.
-
Calculate the volume of right prisms.
HintsThe volume of a prism is, $V=Bh$, where $B$ represents the area of the base and $h$ represents the height of the prism. The area of the base is different for each type of prism.
The volume for the rectangular prism above is,
- $V=lwh$
- $V=15~\text{in}\cdot 3~\text{in}\cdot 13~\text{in}$
- $V=585~\text{in}^3$
The volume for the triangular prism above is,
- $V=\frac{1}{2}\cdot b\cdot h_{1}\cdot h_{2}$
- $V=\frac{1}{2}\cdot 27~\text{in}\cdot 11~\text{in}\cdot 42~\text{in}$
- $V=6,237~\text{in}^3$
SolutionThe volume of a prism is $V=Bh$, where $B$ represents the area of the base and $h$ represents the height of the prism.
1. The rectangular prism with a length of $27$ inches, a width of $9$ inches, and a height $14$ inches has a volume of,
- $V=lwh$
- $V=27~\text{in}\cdot 9~\text{in}\cdot 14~\text{in}$
- $V=3,402~\text{in}^3$
- $V=\frac{1}{2}\cdot b\cdot h_{1}\cdot h_{2}$
- $V=\frac{1}{2}\cdot 42~\text{in}\cdot 19~\text{in}\cdot 51~\text{in}$
- $V=20,349~\text{in}^3$
- $V=lwh$
- $V=24~\text{in}\cdot 7~\text{in}\cdot 11~\text{in}$
- $V=1,848~\text{in}^3$
- $V=s\cdot s\cdot s$
- $V=13~\text{in}\cdot 13~\text{in}\cdot 13~\text{in}$
- $V=2,197~\text{in}^3$
- $V=\frac{1}{2}\cdot b\cdot h_{1}\cdot h_{2}$
- $V=\frac{1}{2}\cdot 37~\text{in}\cdot 30~\text{in}\cdot 17~\text{in}$
- $V=9,435~\text{in}^3$
-
Solve real-world problems involving the volume of right prisms.
HintsThe volume of a prism is, $V=Bh$, where $B$ represents the area of the base and $h$ represents the height of the prism.
- The area of a rectangular base is, $B=lw$.
- The area of a triangular base is, $B=\frac{1}{2}bh$.
The volume of a box that is $5$ feet long, $3$ feet wide and $7$ feet high is,
- $V=lwh$
- $V=5~\text{ft}\cdot 3~\text{ft}\cdot 7~\text{ft}$
- $V=105~\text{ft}^3$
The volume of a $6$ foot long tent with a triangular face that measures $4$ feet along the base and $5$ feet high is,
- $V=\frac{1}{2}\cdot b\cdot h_{1}\cdot h_{2}$
- $V=\frac{1}{2}\cdot 4~\text{ft}\cdot 5~\text{ft}\cdot 6~\text{in}$
- $V=60~\text{ft}^3$
Solution1. A family is moving from New York to California and is renting a truck to transport their boxes and furniture. The truck measures $26$ feet long, $8$ feet high and $7$ feet wide. The volume inside the truck is $1,456~\text{ft}^3$.
- To calculate the volume, you should recognize that the back of a moving truck is shaped like a rectangular prism.
- The volume of a rectangular prism is, $V=lwh$.
- Therefore the volume is $V=26~\text{ft}\cdot 8~\text{ft}\cdot 7~\text{ft}=1,456~\text{ft}^3$.
- To calculate the volume, you should recognize that a box of Tobblerone chocolate is shaped like a triangular prism.
- The volume of a triangular prism is, $V=\frac{1}{2}\cdot b\cdot h_{1}\cdot h_{2}$.
- Therefore the volume is $V=\frac{1}{2}\cdot 1.3~\text{in}\cdot 1.4~\text{in}\cdot 8.3~\text{in}=7.533~\text{in}^3$.
- Box A is $20$ inches long, $8$ inches wide, and $7$ inches high.
- Box B is $15$ inches long, $12$ inches wide, and $5$ inches high.
- To calculate the volume, you should recognize that a box is shaped like a rectangular prism.
- The volume of a rectangular prism is, $V=lwh$.
- The volume for Box A is $V=20~\text{in}\cdot 8~\text{in}\cdot 7~\text{in}=1,120~\text{in}^3$.
- The volume for Box B is $V=15~\text{in}\cdot 12~\text{in}\cdot 5~\text{in}=900~\text{in}^3$.
- Since $1,120~\text{in}^3$ is greater than $900~\text{in}^3$, Jordan picks Box A.
-
Review the area of shapes and names of 3-D objects.
HintsThe name of a 3-D prism generally includes the shape of their base. However, there are a few exceptions.
To calculate the area of a triangle we need to know the dimensions of its base and height.
The area of a circle with a radius of $2$ cm is approximately equal to $12.57$ cm$^2$.
A cone is a solid or hollow object which tapers from a circular base to a point.
A cylinder is a solid object with:
- two identical flat ends that are circular
- and one curved side.
SolutionBlue Square*
- The area of a square with side lengths, $s$, is $A=s^2$.
- A cube and a square prism are two 3-D shapes with a square base.
- The area of a rectangle with length $l$ and width $w$ is $A=lw$.
- A rectangular prism is a 3-D shape with a rectangular base.
Pink Triangle
- The area of a triangle with base $b$ and height $h$ is, $A=\frac{1}{2}bh$.
- A triangular prism is a 3-D shape with a triangular base.
- The area of a circle with radius $r$ is, $A=\pi r^2$.
- A cylinder and a cone are two 3-D shapes with a circular base.
-
Calculate the volume of the 3-D object.
HintsThe volume of a prism is, $V=Bh$, where $B$ represents the area of the base and $h$ represents the height of the prism.
The base area is represented many different ways, and is dependent on the base shape of the prism.
Two rectangular prisms that are attached together is called a composite rectangular prism. Multiple volumes of rectangular prisms make up the volume of a composite rectangular prism.
SolutionThe volume of a prism is $V=Bh$, where $B$ represents the area of the base and $h$ represents the height of the prism.
1. Composite Rectangular Prism
The volume of the first rectangular prism with dimensions $7~\text{cm}$ by $2~\text{cm}$ by $5~\text{cm}$ is,
- $V=[lw]h$
- $V=7~\text{cm}\cdot 2~\text{cm}\cdot 5~\text{cm}$
- $V=70~\text{cm}^3$
- $V=[lw]h$
- $V=4~\text{cm}\cdot 4~\text{cm}\cdot 2~\text{cm}$
- $V=32~\text{cm}^3$
- $V=70~\text{cm}^3+32~\text{cm}^3=102~\text{cm}^3$
- $V=[\pi \cdot r^2]\cdot h$
- $V=3.14 \cdot 3~\text{cm}^2\cdot 9~\text{cm}$
- $V=254.34~\text{cm}$
- $V=[\frac{1}{2}(b_1+b_2)\cdot h_{1}]\cdot h_{2}$
- $V=\frac{1}{2}(6~\text{cm}+9~\text{cm})\cdot 5~\text{cm}\cdot 18~\text{cm}$
- $V=675~\text{cm}^3$
- $V=[\frac{1}{2}\cdot b\cdot h_{1}]\cdot h_{2}$
- $V=\frac{1}{2}\cdot 20$cm$\cdot 12~\text{cm}\cdot 25~\text{cm}$
- $V=3,000~\text{cm}^3$


















@Samayah frfr no cap
"Call now to receive your shipment of premium, evil piranhas! But wait, if you order within the next 3 minutes, you'll receive the best discount ever! Don't miss this amazing deal-of-a-lifetime!" can the sofatutor team plzzz make this an ad for YT or TNF? this is hilarious
LMAO WHYYYY PIRANHAS???
WHO WANTZ EVIL PIRANHAS
and also its toy fish bruh