Surface Area of Prisms, Cubes, and Boxes

Basics on the topic Surface Area of Prisms, Cubes, and Boxes
The total surface area of a prism is the sum of the areas of its lateral faces and its two bases, which is not so different from the cube or box. A cube is a prism having six square faces (both lateral faces and bases), thus its surface area is the sum of the areas of its six square faces. A box is a prism having 3 pairs of congruent faces, namely two pairs of its lateral faces and its bases; thus, its surface area is twice the sum of the areas of the three faces with their congruent pair. Learn how to calculate surface area of a prism, cube, and box by helping Sam Torpintino, an aspiring movie director, keeps his movie map just right in order to impress the studio executive for his new movie idea, “Attack of the Really Really Big Slugs from Outer Space” . Common Core Reference: CCSS.MATH.CONTENT.6.G.A.4
Transcript Surface Area of Prisms, Cubes, and Boxes
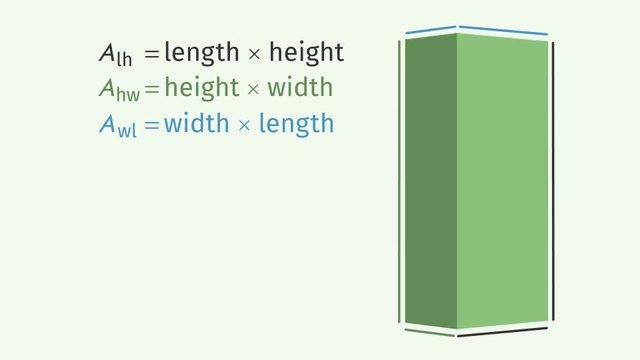
Sam Torpintino is an aspiring movie director who is looking for his big break. He’s pitching his latest idea to a big time studio executive: Attack of the Really, Really Big Slugs from Outer Space, but the studio executive needs a bit of convincing. In Torpintino’s new movie, a famous scientist, Navy SEAL, and men’s fashion model is elected President, but on his first day in office, the world is attacked by an onslaught of really, really big space slugs. In order to save the city, he hatches a plan to cover all the buildings in a thin layer of salt, which will protect the city from the slugs’ slime. However, to get the math just right, the director needs our help with calculating the surface area of prisms, cubes and boxes. The calculations for the surface area of cubes and boxes are not so different from each other. Each of these shapes has 6 total sides. There’s a top and bottom, a right and left face, and a front and back face. Surface area is just the sum of the areas of each of the faces. The area of each face is calculated by multiplying the two dimensions that make up the face, length times height, height times width, or width times length. If we just look at this face of the building, the length is 85 feet and the height is 190 feet. 85 times 190 is 16,150 square feet. But this was just the front face, so we need to multiply it by two to get the back face as well. This gives us 32,300 square feet. By rotating the box a bit, we see that there are two more areas that need to be calculated. Multiplying a height of 190 feet times a width of 50 feet, we get 9,500 square feet. Again, we multiply this result by two to get 19,000 square feet, since there is another face that's the same size. The only thing that’s left is the top and bottom. This time, we multiply the width of 50 feet times the length, 85 feet, giving us 4,250 square feet. Again, we multiply this result by two, providing us with an additional 8,500 square feet. By summing all the areas, we get the total surface area of the building. But, since we don't have to cover the bottom of the building in salt, we can subtract the surface area of the base, giving us 55,550 square feet. The process of finding surface area for a box is often represented by the formula: Surface area equals two times the length times width, plus two times the height times length, plus two times the width times height. But this can be written shorter by using the first letter of each dimension like this. Finding the surface area of a cube is very similar, and a bit easier. We can start with the formula we found for the surface area of a box. But since the length, width, and height of a cube are all the same, we can use the same value to calculate the area of each face. Let's just call that value "side". A cube has the same number of faces as a box, but each has the area of side times side, so we can simply multiply 6 times the length of a side squared, to obtain the total surface area. Not all of the buildings in the city, however, are shaped like boxes and cubes. There are a few more eccentric structures that have triangular shapes on the top and bottom, like this. Fortunately, calculating the surface area of these structures, known as prisms, is very similar to what we’ve already done. But in this case, we just have three sides and a top and bottom. So we can calculate the surface area by calculating 3 times the height times the triangle side length for the rectangular faces and adding two times the area of the triangular top and bottom, which, if you remember, is one-half the base of the triangle times the height of the triangle. Normally, we'd need to multiply the area of the triangle face by two to get the full surface area, but like before, we don't need to cover the base of the building in salt, so we leave that out of our expression. This weird-looking building is 100 feet tall and has a rectangular side length of 36.5 feet. The roof and floor of the building are equilateral triangles with a side length of 36.5 ft. The height of this equilateral triangle is 31.61 feet. So, after multiplying and combining like terms, if our hero collects 11,526.8825 square feet of salt for this building, he’ll be able to keep the slugs at bay. Let’s check back in with Sam Torpintino and see how the pitch is going. It looks like Sam Torpentino is showing off what he wants to do for the climactic scene of his movie, but the studio executive doesn’t look impressed. Yeah, but can you really blame him? Who would ever greenlight a movie all about surface area and giant slugs…??
Surface Area of Prisms, Cubes, and Boxes exercise
-
Determine the surface area of the given rectangular prisms and cubes.
HintsThe area of face $ A $ is $ 5 \times 8 $, or $40 ~\text{units squared}.$ There are $2$ of these, so that's $ 80 ~\text{units squared}.$
The area of face $ B $ is $ 6 \times 8 $, or $48 ~\text{units squared}.$ There are two of those, so that's $ 96 ~\text{units squared}.$
The area of face $ C $ is $ 5 \times 6 $, or $ 30 ~\text{units squared}.$ There are two of those, so that's $ 60 ~\text{units squared}.$
The total surface area is $80+96+60$, or $236 ~\text{units squared}.$
The cube shown has side length $ 3 $. The area of face $ D $ is $3 \times 3 $, that is, $ 3^2 $, or $9$.
There are six such faces, so the total surface area is $ 6 \times 9$, or $ 54 ~\text{units squared}$.
The total surface area of the rectangular prism shown is the sum of the areas of each labelled face ($A$, $B$, $C$), DOUBLED.
The total surface area is given by the following equation:
$SA = 2lh + 2wh +2lw$
The total surface area of a cube is $6$ times the area of one face. The area of face $D$ is $s \times s$, or $s^2$. There are six such faces, so the total surface area is $6s^2$.
SolutionThe surface area of the rectangular prism shown is given by the formula:
$ SA = 2lh + 2wh +2lw $.
For the first problem, $l=3$, $w=4$, and $h=5$. Therefore:
$ SA = 2lh + 2wh +2lw $. $ SA = 2(3\times5) +2(4\times5)+2(3\times4) $. $ SA =2(15) + 2(20) +2(12) $ $ SA =30 +40 +24 $ $ SA = 94 ~\text{units squared}$
The surface of the cube shown is given by the equation:
$SA =6s^2$
For the second problem, $s=2$, therefore:
$SA = 6(2^2)$ $SA = 6(4)$ $SA =24 ~\text{units squared}$
-
Explain how to calculate the surface area of the triangular prisms.
HintsA rectangular prism is composed of two triangular bases (orange in the diagram), and three rectangular faces (blue in the diagram).
The area of a triangle is $\frac{1}{2}bh$. The height is always perpendicular to the base. If the area of one triangle is $\frac{1}{2}bh$, the area of two such triangles is $2\cdot\frac{1}{2}bh$, or $bh$.
A triangular prism has three lateral faces that are rectangles. The height of the rectangles is the same for each. The areas of the rectangles in the diagram are $ah$, $bh$, and $ch$.
SolutionThe triangular base of the first prism has a base length of $6$ and a height of $4$. So the area of the triangle is $\frac12(6)(4)=12$. There are two such triangles and the area of the two triangles combined is $24$. There are two $5\times10$ rectangular faces. Each has an area of $50$. The remaining rectangular $6\times10$ face has an area of $60$. The total surface area is $24 + 100 + 60 =184 ~\text{units}^2$.
The second prism has a triangular base whose area is $\frac{1}{2}bh$. There are two such triangles, so their combined area is $2\cdot\frac{1}{2}bh$, or $bh$. There are two rectangular faces with area $wl$, and one with area $bl$. The total surface area is $bh+2wl+bl$.
-
Solve for the surface area of the 3-D objects.
HintsThe surface area of a rectangular prism with dimensions $lwh$ is $2lw+2lh+2wh$.
The surface area of the triangular prism shown is twice the area of the base, plus the area of the three lateral faces (the rectangles).
$SA=2\cdot \frac{1}{2}bh + al + bl + cl$
This simplifies to:
$SA=bh + al + bl + cl$
SolutionThe smallest figure is rectangular prism with dimensions $3\times10\times1$.
$SA=2\cdot(3)(10)+2\cdot(3)(1)+2\cdot(10)(1)$
$SA=2\cdot30+2\cdot3+2\cdot10$
$SA=60+6+20$
$SA=86 ~\text{u}^2$
The next largest figure is the triangular prism with a triangular base with sides lengths of $5$, $12$, and $13$.
$A_\text{triangle}=\frac{1}{2}(12)(5)$
$A_\text{triangle}=(6)(5)$
$A_\text{triangle}=30$
$A_\text{two triangles}=2\cdot30$
$A_\text{two triangles}=60$
$SA=60+(5)(1)+(12)(1)+(13)(1)$
$SA=60+5+12+13$
$SA=90 ~\text{u}^2$
The third largest figure is the rectangular prism with dimensions $3\times4\times5$.
$SA=2\cdot(3)(4)+2\cdot(4)(5)+2\cdot(3)(5)$
$SA=2\cdot12+2\cdot20+2\cdot15$
$SA=24+40+30$
$SA=94 ~\text{u}^2$
The largest figure is the triangular prism with a triangular base with base length $12$ and height $8$.
$A_\text{triangle}=\frac{1}{2}(12)(8)$
$A_\text{triangle}=(6)(8)$
$A_\text{triangle}=48$
$A_\text{both triangles}=96$
$SA=96+(12)(1)+10(1)+10(1)$
$SA=96+12+10+10$
$SA=128 ~\text{u}^2$
-
Apply surface area to real world problems.
HintsIf the top and bottom of a rectangular prism have dimensions $l\times w$, with a height of $h$, we can represent such a prism with the diagram shown. The surface area is given by the formula:
$SA=2lw+2wh+2lh$
The prism shown has dimensions $l\times w\times h$. Suppose we are only interested in the lateral area, the four shaded rectangles. If we unfold the figure as shown, we can see that they form a large rectangle, the base of which is equal to the perimeter of the base of the original prism. That's $2l+2w$. To find the lateral area, we multiply this perimeter times the height. So the lateral area of a rectangular prism is the perimeter of the base times the height.
$A_\text{lateral}=(2l+2w)h$
How much greater is the lateral area of the prism on the right than that of the prism on the left? The perimeter of each base is $10$ units. The prism on the left is 5 units tall, while the prism on the right is $7$ units tall. The prism on the right is $2$ units taller than the one on the left. To find the difference in lateral area, shaded red, we multiply the perimeter of $10$ times a height of $2$. That's $20 ~\text{u}^2$.
SolutionFor the first problem, we know the prism has a base that is $5\times7$ and a height of $10$.
$SA=2\cdot(5)(7)+2\cdot(5)(10)+2\cdot(7)(10)$
$SA=2\cdot35+2\cdot50+2\cdot70$
$SA=75+100+140=315 ~\text{in}^2$
For the second problem, the pond is $10\times20$ with a height of $5$. We are interested in the lateral area, that is, the area of the four rectangles that are NOT the top and bottom. We can calculate the area of two of the adjacent rectangles then double those values:
$A_1=(10)(5)=50$
$A_2=(20)(5)=100$
$A_\text{lateral}=2\cdot50+2\cdot100$
$A_\text{lateral}=100+200=300 ~\text{ft}^2$
Another way is to calculate the perimeter of the base, then multiply times the height:
$P=2\cdot10+2\cdot20=60$
$A_\text{lateral}=60\cdot5=300 ~\text{ft}^2$
For the third problem, the perimeter of each base is $50$. The height of the first prism is $3$ and the height of the second is $5$, and we are interested in the difference. That's the lateral area of the prism shaded in red, with a a height of $2$.
$A_\text{lateral}=50\cdot2=100 ~\text{m}^2$
For the fourth problem, we have a prism that is $10\times12\times3$. We can frost all faces except the bottom. We could find the area of each rectangular face and add them. We can also find the lateral area using the perimeter of the base, then add the area of one base.
$P=2\cdot10+2\cdot12=44$
$A_\text{lateral}=44\cdot3=132$
$A_\text{top}=(12)(10)=120$
$A_\text{frosting}=252 ~\text{in}^2$
-
Find the area of rectangles and triangles.
HintsThe area of a rectangle is base times height. That's $A = bh $.
The area of a triangle is half the base times the height. That's $A = \frac{1}{2}bh $.
Even if the triangle is obtuse, and the height of the triangle is drawn outside of the triangle, the area is still half the base times the height. Extending the base with a dotted line helps us visualize the height.
The units for area are square units, like $\text{ft}^2$, $\text{km}^2$, and $\text{cm}^2$. Cubic units like $\text{ft}^3$ are for volume, and units like $\text{ft}$ are for length.
SolutionThe area of the first triangle is half the base times height.
$A = \frac{1}{2}(4)(3) $
$ A= 6 ~\text{cm}^2 $
The area of the rectangle is base times height.
$A = (4)(3) $
$A = 12 ~\text{cm}^2 $
The area of the next figure, a triangle, is half base times height.
$A = \frac{1}{2}(4)(3) $
$ A = 6 ~\text{cm}^2 $
The area of the last figure, a triangle, is half base times height.
$ A = \frac{1}{2}(6)(4) $
$ A = 12 ~\text{cm}^2 $
-
Find the surface area of prisms and cylinders.
HintsTo find the surface area, we can always find the area of each face, but with fractions like this, there is a better way. First, let's choose the $\frac14 \times \frac14$ face as the base.
$A_\text{base}=(\frac14)(\frac14)=\frac18$
$A_\text{two bases}=\frac18+\frac18=\frac14$
The lateral area (the area of the remaining rectangles that are not the base) is the perimeter of the base, times the height.
$P=4\cdot\frac14=1$
$A_\text{lateral}=(1)(7 \frac12)=7 \frac12$
$SA=\frac14+7\frac12$
$SA=0.25+7.5=7.75~\text{units}^2$
The surface area of a cylinder can be found by finding area of the bases, and then finding the lateral area. To find the lateral area, we will use the method described in the last tip. We find the perimeter of the base, and multiply times the height. The base of a cylinder is a circle, and the perimeter of a circle is called circumference. Here are two useful formulas:
$A_\text{circle}=\pi r^2$
$P_\text{circle}=C=2 \pi r$
The area of the base in this diagram is $\pi r^2$. There are two of them, so that's $2\pi r^2$. The lateral area is the circumference of $2\pi r$ times the height of $h$. That's $2 \pi r h$. Therefore:
$SA_\text{cylinder}=2 \pi r^2 + 2 \pi r h$.
SolutionFor the first figure, let's select the $\frac12 \times \frac12$ face as the base.
$A_\text{base}=(\frac12)(\frac12)=\frac14$
$A_\text{two bases}=2\cdot\frac14=\frac12$
Let's find the lateral area by finding the perimeter of the base and multiplying by the height of $9 \frac12$.
$P=4\cdot\frac14=1$
$A_\text{lateral}=(2)(9 \frac12)=19$
$SA=19 +\frac12=19\frac12=19.5~\text{units}^2$
For the second figure, let's first find the area of the triangular base:
$A_\text{base}=\frac12(1)(\frac34)$
$A_\text{two bases}=2\cdot\frac12(1)(\frac34)$
$A_\text{two bases}=\frac34$
Now let's find the lateral area by finding the perimeter of the base and multiplying by the height.
$P=1+\frac34+1\frac14=3$
$A_\text{lateral}=3\cdot2=6$
$SA=6+\frac34=6.75~\text{units}^2$
For the third figure, we find the area of the base, a circle, and double it. Then we find the perimeter of the base, otherwise known as the circumference, and multiply times the height.
$A_\text{circle}=\pi(5)^2=25\pi$
$A_\text{two circles}=2\cdot25\pi=50\pi$
$C=2\pi(5)=10\pi$
$A_\text{lateral}=10\pi\cdot20=200\pi$
$SA=200\pi+50\pi=250\pi~\text{units}^2$
For the last figure, we are given the area and the perimeter of the base.
$A_\text{base}=16$
$A_\text{two bases}=32$
$P=20$
$A_\text{lateral}=20 \cdot 10 =200$
$SA=200+32=232~\text{units}^2$