Volume of Simple 3D Shapes
- Volume of a 3D Shape
- Understanding Volume – Definition
- Volume Formulas for 3D Shapes – Examples
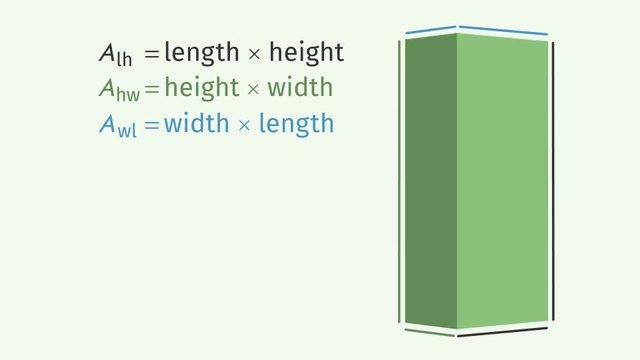
- Volume of a Rectangular Prism
- Volume of a Cube
- Volume of a Triangular Prism
- Volume of a Cylinder


Basics on the topic Volume of Simple 3D Shapes
Volume of a 3D Shape
Volume is a fundamental concept in geometry and everyday life, allowing us to quantify the three-dimensional space occupied by an object. From filling a swimming pool to baking a cake, understanding volume is essential for a myriad of activities.
Understanding Volume – Definition
Volume is the measure of the amount of space an object occupies in three dimensions. It’s commonly measured in cubic units, such as cubic centimeters (cm$^3$), cubic feet (ft$^3$), or cubic liters (l$^3$).
In terms of mathematics, volume is a property of three-dimensional shapes, and calculating it often requires knowledge of certain formulas that apply to these shapes.
Volume Formulas for 3D Shapes – Examples
There are all different types of 3D shapes and each of them uses a different formula to calculate the volume. Here is a table showing some common 3D shapes, what they look like and the formula used to find their volume.
| Shape | Description | Volume Formula | Illustration Request |
|---|---|---|---|
| Rectangular Prism | A box-shaped figure | $V = l \times w \times h$ |  |
| Cube | A six-sided figure with equal sides | $V = s^{3}$ | 
|
| Triangular Prism | A prism with triangular bases | $V = \frac{1}{2} \times b \times h \times l$ |  |
| Cylinder | A circular solid figure | $V = \pi \times r^{2} \times h$ |
 |
Volume of a Rectangular Prism
Example: Find the volume of a rectangular prism with a length of 10 cm, a width of 4 cm, and a height of 5 cm.
Solution:
Identify the dimensions: Length = 10 cm, Width = 4 cm, Height = 5 cm.
Apply the volume formula for a rectangular prism: Volume = Length x Width x Height.
Calculate: Multiply the dimensions: 10 cm x 4 cm x 5 cm = 200 cm³.
Result: The volume of the rectangular prism is 200 cm³.
Volume of a Cube
Example: Find the volume of a cube with sides of length 3 cm.
Solution:
Identify the length of the side: The side length is 3 cm.
Apply the volume formula for a cube: Volume = Side$^{3}$.
Calculate: Cube the side length: 3 cm x 3 cm x 3 cm = 27 cm$^{3}$.
Result: The volume of the cube is 27 cm$^{3}$.
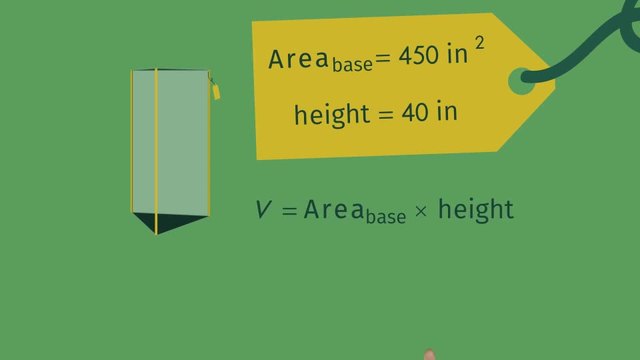
Volume of a Triangular Prism
Example: Find the volume of a triangular prism with a base of 6 cm, a height of the triangle of 4 cm, and a length of 10 cm.
Solution: 1. Identify the dimensions: Base = 6 cm, Height of the triangle = 4 cm, Length = 10 cm.
Apply the volume formula for a triangular prism: Volume = $\frac{1}{2} \times \text{Base} \times \text{Height of the triangle} \times \text{Length}$.
Calculate: Multiply the dimensions: $\frac{1}{2} \times 6 \text{cm} \times 4 \text{cm} \times 10 \text{cm} = 120 \text{cm}^{3}$.
Result: The volume of the triangular prism is 120 cm³.
Volume of a Cylinder
Example: Find the volume of a cylinder with a radius of 5 cm and a height of 7 cm.
Solution:
Identify the dimensions: Radius = 5 cm, Height = 7 cm.
Apply the volume formula for a cylinder: Volume = $\pi \times \text{Radius}^{2}\times \text{Height}$.
Calculate: Multiply the dimensions: $\pi \times(5\text{cm})^{2} \times 7 \text{cm} \approx 549.78 \text{cm}^{3}$.
Result: The volume of the cylinder is approximately 549.78 cm³.
Volume of Simple 3D Shapes – Practice
Volume of Simple 3D Shapes – Summary
Key Learnings from this Text:
- Volume measures the space occupied by a 3D object and is expressed in cubic units.
- For simple 3D shapes, specific formulas allow us to calculate their volume.
- These principles have practical applications in various fields from engineering to daily tasks.
- Understanding and calculating volume is crucial for efficient space management.
Volume Formulas for Simple 3D Shapes – Frequently Asked Questions
Transcript Volume of Simple 3D Shapes
The Mad Hatter is a world-renowned milliner...he makes hats and news of his brilliance has reached the queen. The queen needs a headpiece for a splendid party she's attending. His creations are always the talk of the town but now, he needs boxes for the hats before they're presented to the queen! To do this, he needs to know how to find the volume of simple three dimensional shapes. For the card hat, he needs a rectangular box for the triangular hat, he needs a triangular box, or prism and for the teapot hat, he needs a circular box, or cylinder. The Mad Hatter decides to put his first fashioning in a rectangular box. Let's help him figure out the volume of the boxes he needs. In order to find the volume of any three-dimensional object, you first have to find the area of the base and then multiply the result by the length of the remaining side, which we'll call height. The dimensions of the first hat are: 12 inches for the length 10 inches for the width and 16 inches for the height. Multiplying these two dimensions gives us the area of our first shape, a rectangle. 12 inches times 10 inches is 120 square inches. Then, we multiply 120 by the remaining side, 16, giving us 1,920. Since we're also multiplying the units the units for the volume of the box are ‘inches cubed’. Next, let’s help the Mad Hatter get his Hatter hat into a triangular box. In order to find the volume of the box, which is in the shape of a triangular prism the concept is the same...find the area of one planar face and multiply that by the remaining dimension. The box measurements are: 24 inches for the base of the triangle 16 inches for the height of the triangle and 18 inches for the height of the box. This time, we need to first find the area of the TRIANGLE and then multiply by the remaining dimension, height. We know the formula to find the area of triangles is one-half times the base times the height. Substituting in our measurements and multiplying gives us 192 square inches for the area of the triangular base. Then, multiplying the area of our triangle, 192 square inches, by the remaining dimension, a height of 18 inches gives us the volume of the triangular prism, 3,456 cubic inches. The Mad Hatter is particularly pleased with his last creation, which he’ll put in a special, round box. For this, we only need two measurements: the radius of the hat and its height. The radius of this hat is 25 inches and it’s 51 inches tall. Just like in the other examples, we need to find the area of one planar face and then multiply the result by the remaining dimension. In this case, our planar face is a circle, so we can substitute the equation for the area of a circle in our general equation for volume. Remember that the area of a circle is given by the formula pi ‘r’ squared. We simply have to plug in the values we know to get the area of the circle and then multiply that area by the remaining measurement, height. Doing so gives us 625π square inches for the area. We then need to multiply this by the height, 51 inches, to get the volume. So a box to hold the teapot hat has to have a volume of 31,875π. If we substitute 'pi' with 3.14... We get 100,087.5 cubic inches as the final volume of the cylindrical box. Okay, to review. When finding the volume of simple shapes you first need to find a face of the shape whose area doesn't change with the height. For each of our shapes, we first found the area of the base and then multiplied the result by the height. The area of the rectangular shape is found by multiplying length times width the area of the triangular base is given by the equation one-half base times height and the equation for the area of a circle is pi 'r' squared. Multiplying each of these areas by height gives us volume. Now that the hats are packed away in boxes, let's see which one the queen has chosen. The queen absolutely LOVES the teapot hat but there's something different about THIS hat...
Volume of Simple 3D Shapes exercise
-
Decide which statements about volume are true.
HintsHere are the formulas for the base area and volume of a rectangular prism.
If you divide a rectangle with a diagonal, you get two congruent triangles. Therefore, each triangle has half the area of the rectangle.
SolutionCalculating the volume of a prism always follows the same general idea:
- First, determine the area of the base: the units will be $in^2$ or $ft^2$ or ...
- Then, multiply this area by the height of the prism, because the base is repeated that many times. The resulting units will be $in^3$ or $ft^3$ or ...
There are several area formulas that are used quite often and should be memorized:
- circle: $A=\pi\cdot r^2$ where $r$ is the radius.
- triangle: $A=\frac12 base_{\Delta}\cdot height_{\Delta}$.
- rectangle: $A=lw$ where $l$ is the length and $w$ is the width.
-
Determine the volume of a cylinder.
HintsThe concept for the calculation of the volume of a prism is always the same:
- Determine the area of the base.
- Multiply this area by the height of the prism.
Because $pi$ is greater than $1$, the result using an approximation of $\pi$ must be greater than the factor by which you multiply $\pi$.
SolutionWe use the volume formula
$V=Area_{\circ}\cdot height_{box}$
- Putting the radius $r=21~in$ in the area formula we get $Area_{\circ}=\pi(25~in)^2=625\pi~in^2$.
- Now we multiply this result by $height_{box}=51~in$. This results in $V=31,875\pi~in^3$.
- Putting $\pi\approx 3.14$ in this result gives us $V\approx 31,875(3.14)~in^3=100,087.5~in^3$.
-
Identify formulas for the 3-D objects and their cross sections.
HintsLook at the labeling of the 3-D shapes.
You have to assign an area as well as a volume formula to each shape.
The volume formula must match the area formula.
SolutionHere you can see all the formulas for area and volume of rectangular prisms, triangular prisms, and cylinders.
Rectangular prism
- The base area is given by $area_{\square}=l\cdot w$.
- We multiply this by the remaining length $h$ to get the volume $V=l\cdot w\cdot h$.
- The base area is given by $area_{\Delta}=base_{\Delta}\cdot height_{\Delta}$.
- We multiply this by the height of the box $h$ to get the volume $V=base_{\Delta}\cdot height_{\Delta}\cdot h$.
- The base area is given by $area_{\circ}=\pi\cdot r^2$.
- We multiply this by the height of the box $h$ to get $V=\pi\cdot r^2\cdot h$.
-
Solve these real world problems.
HintsFor the volume of a rectangular prism, just multiply the side lengths
$V=l\cdot w\cdot h$.
Pay attention when rounding numbers:
- $3.1415$ rounded to two decimal places results in $3.14$.
- $2.71828$ rounded to two decimal places results in $2.72$.
Use the circumference formula for a circle:
$C=2\cdot \pi\cdot r$.
Substitute the value for the circumference and solve for the radius.
The volume of a cylinder is given by
$V=\pi\cdot r^2\cdot h$
where $r$ is the radius and $h$ the height of the cylinder.
SolutionPool 1 For this pool we just have to multiply the side lengths:
$V=(48~in)^2\cdot (12~in)=27,648~in^3$
Pool 2 Since this pool is a cylindrical prism, we have to use the volume formula for cylinders
$V=\pi\cdot r^2\cdot h$
where $r$ is the radius and $h$ the height of the cylinder. Plugging in the known values we get
$V=\pi\cdot (36~in)^2\cdot (8~in)= 10,368 \pi~in^3\approx10,368 \cdot 3.14~in^3= 32,555.52 ~in^3$
Thus, we can conclude that the square prism holds less water than the cylinder.
$ $
A standard $8.5$ by $11$ inch sheet of paper
Cylinder A is formed by bringing the two longer sides around together.
So we can determine the radius with $8.5=2\cdot \pi\cdot r$. Dividing by $2\cdot pi\approx 2\cdot 3.14=6.28$ we get $r\approx 1.35~in$.
Now we can put this in the volume formula for cylinders we used above:
$V=\pi\cdot (1.35~in)^2\cdot (11~in)= 20.0475 \pi~in^3\approx20.0475 \cdot 3.14~in^3\approx 62.95 ~in^3$
Cylinder B is formed by bringing the two shorter sides together.
Here we determine the radius by using $11=2\cdot \pi\cdot r$. Dividing by $2\cdot pi\approx 2\cdot 3.14=6.28$ we get $r\approx 1.75~in$.
Now we can put this in the volume formula for cylinders from above:
$V=\pi\cdot (1.75~in)^2\cdot (8.5~in)= 26.03125 \pi~in^3\approx 26.03125 \cdot 3.14~in^3\approx 81.74 ~in^3$
-
Identify the shapes.
HintsEach prism has a base and a top face which are congruent.
A pyramid has a base and a peak.
Each corner of the base, for example a square or a rectangle, is connected with this peak.
Here you see a sphere. This is not a prism.
SolutionWhat are the common features of prisms?
- The bottom and top faces are congruent.
- They consist of the bottom and top faces, plus several rectangles or a curved surface
A cube has only squares as faces. All of the six faces are congruent.
A prism with a circle as the bottom and top face is called a cylinder.
Last, we have to investigate a prism with triangles as the bottom and top faces: This is a triangular prism.
-
Find mistakes in the volume calculations.
HintsDon't forget about units! Each time you multiply an area ($in^2$) by a length ($in$), you also have to multiply the units.
The formula for the area of a circle is $A=\pi\cdot r^2$.
There are seven mistakes in total.
SolutionMr. Joke's cylinder:
The radius is $r=1.4~in$ and the height $h=2.5~in$.
So we get for the volume
$V=\pi\cdot (1.4~in)^2\cdot (2.5~in)=4.9\pi~in^3\approx 15.4~in^3$
(in the problem above, the radius and height were switched!)
Don't forget about the units: it's $in^3$.
$~$
Paul's Lunchbox:
- First, we multiply all side lengths to get the volume
- Because we know the volume of one slice of bread, $12~in^3$, we just have to divide $48~in^3$ by $12~in^3$ to get the number of slices of bread: It's $4$, not $6$!
Carol's Carrot Cake:
- The formula for a triangle's area is given by $A=\frac12\cdot base_{\Delta}\cdot height_{\Delta}=\frac12(3~in)\cdot(3~in)=4.5~in^2$
- This area must be multiplied by the height $h=6~in$ to get $V=(4.5~in^2)\cdot (6~in)=27~in^3$