The Unit Rate as the Scale Factor


Basics on the topic The Unit Rate as the Scale Factor
After this lesson you will be able to calculate the scale factor in a scale drawing, and create a scale drawing with a given scale factor.
The lesson begins by teaching you that a scale factor is needed to make an enlargement. It leads to calculating unit rates and determining if the unit rates can be used as a scale factor. It concludes with using a scale factor to make a reduction.
Learn about using unit rates as scale factors by helping Junior get his giant rat into a carrying case!
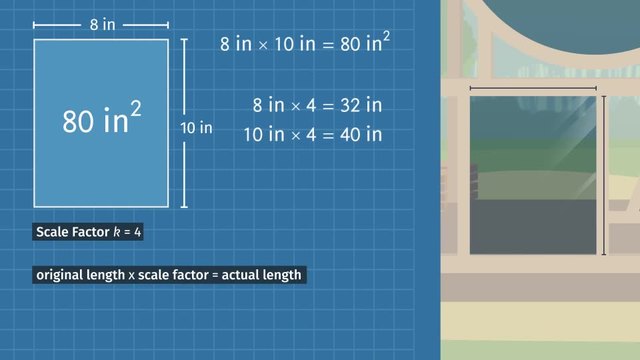
This video includes key concepts, notation, and vocabulary such as: scale factor (also known as the constant of proportionality, is the ratio of any length in the scale drawing to the corresponding length in the actual picture); ratio (a comparative, proportional relationship between two amounts); reduction (a scaled-down picture of the original image); and enlargement (a scaled-up picture of the original image).
Before watching this video, you should already be familiar with equivalent ratios, recognizing if a fractional scale factor is greater than or less than 1, and multiplication and division involving fractions.
After watching this video, you will be prepared to learn how to find missing dimensions in a scale drawing, given the scale factor and dimensions of the original image.
Common Core Standard(s) in focus: 7.RP.A.2b A video intended for math students in the 7th grade
Transcript The Unit Rate as the Scale Factor
Phase one of Junior Moranis's science fair project is now officially complete. Using a growth ray he found in his dad's laboratory, he has successfully enlarged his pet rat, Peter. But now, the question is how can Junior get this giant rat into his normal-sized carrying case so he can submit his project to the science fair? To answer that question, we're going to have to use the unit rate as the scale factor. Junior has already taken the measurements of his carrying case. The height and width are both a foot and a half and the length is two and a half feet. Junior has also measured his pet rat and thinks that he’ll need to enlarge the case so that its new dimensions are 3 by 3 by 5. In order to use the growth ray and make an enlargement of this size, what scale factor should he use? Since a scale factor is just the constant of proportionality between the dimensions of a scaled object to the original we can find it by determining the ratio of any length in the enlarged version to the corresponding length in the original. So let’s calculate some unit rates and see if they reveal a constant of proportionality which we can use as our scale factor. To begin, be sure to create a ratio of corresponding measurements. That is, height to height width to width or length to length. Also, remember we always create ratios of the scaled object to the original. Here, the ratio of the height of the enlargement to the height of the original is 3 to 1-and-a-half. When dividing fractions, we write whole numbers as fractions over 1, so 3 becomes 3 over 1. Then, we convert mixed numbers to improper fractions, so 1 and a half becomes 3 halves. Then we multiply by the reciprocal of the denominator, 2 thirds, and simplify. The result of our division is 2. Now, let's look at the widths. The ratio of enlarged width to original is also 3 to 1-and-a-half, so dividing as before gives us a unit rate of 2. Looking at the lengths, the ratio of enlargement to original is 5 to 2-and-a-half. That’s 5 over 1, over 5 halves. Multiplying by two-fifths, our division once again gives us a unit rate of 2. Since we got the same answer when computing each rate, we have a constant of proportionality, or scale factor 'k', of 2. Remember scale factors greater than 1 result in enlargements and because our scale factor is 2 for every dimension, we have a true enlarged version of the original. We can confirm this by noting that multiplying each dimension of the original by two gives us the corresponding dimension in the enlargement. In his new luxurious carrying case, Peter is ready to be shipped off to the science fair! But Junior has one more sizeable problem to solve before he can go. He has already designed an impressive poster for his project but his teacher insists that he reduce it by a scale factor of one-third. Let’s help Junior scale down his poster so he can get to school and unveil his scientific breakthrough. The poster as he designed it has a gargantuan height of 9 feet. It’s got two side flaps that are each 3 feet wide there is a central rectangle that is 6 feet wide and a circular picture in the middle with a radius of 2 and a quarter feet. We need to create a reduction that is one-third the size of the original. So if we multiply each dimension of the original by a scale factor of one-third, we’ll get the corresponding dimensions of the reduction. Let's start with the height. 9 times one-third is 3, so that will be our reduced height. For the side width, 3 times a third is 1. And for the central width, 6 times one-third reduces to 2. Now for the circular picture. Let’s convert the radius of the circle to an improper fraction, 9 fourths. Multiplying by our scale factor of one-third, we can cross-cancel and the reduced radius of the circle will be 3 fourths. Note that the scale factor was a value between 0 and 1 so we know we created a reduction. To review: A scale factor is the same as the constant of proportionality, just applied to the dimensions of geometric objects. We can divide corresponding measurements to find the scale factor between two proportional objects. We can also multiply by a given scale factor to reduce or enlarge a geometric shape. If the scale factor is greater than 1, it results in an enlargement and if the scale factor is between 0 and 1, it results in a reduction. Meanwhile, back at the science fair which seems to have ended prematurely. Well you've got to expect that a scaled-up rat is going to have a scaled-up appetite. That's just science.