How to Create a Scale Drawing
- Introduction to Scaling Drawings
- Understanding Scaling in Drawing – Definition and Importance
- The Fundamentals of Scaling


Basics on the topic How to Create a Scale Drawing
Introduction to Scaling Drawings
Scaling a drawing is an essential skill for architects, engineers, artists, and hobbyists alike. It allows for the precise increase or decrease of an image's size while retaining its original proportions, shape, and detail. Whether you're creating a large mural from a small sketch or fitting a landscape into a miniature painting, understanding how to scale drawings is vital.
Understanding Scaling in Drawing – Definition and Importance
Scaling in a drawing refers to the proportional enlargement or reduction in the size of an image.
It's crucial in the world of art and design because it helps in visualizing projects at different scales, making replicas, and adjusting the size of images to fit specific formats or spaces.
The Fundamentals of Scaling
Scaling involves mathematically adjusting the dimensions of an image using a scale factor. This could mean doubling, tripling, or halving the size, among other variations.
Accurate scaling ensures that the integrity and aesthetics of the original drawing are preserved, regardless of its new size.
Scaling a Drawing with a Ruler – Example
Scale a 4x6 inch photo to twice its original size.
- Measure the original dimensions: The photo measures 4 inches by 6 inches.
- Determine the scale factor: The desired scale factor is 2 (twice the size).
- Calculate the new dimensions: Multiplying each dimension by the scale factor gives us 8 inches by 12 inches.
- Transfer the measurements to drawing paper: Mark the new dimensions on the larger paper and connect the dots to create the scaled-up outline.
To ensure accuracy, draw a grid over the original image and the new, larger paper with corresponding grid squares. This will help in transferring each part of the image accurately.
Scale an 8x12 inch map to half its original size using a scale factor of 0.5 or $ \frac{1}{2} $.
- Measure the original dimensions: The map measures 8 inches by 12 inches.
- Determine the scale factor: The desired scale factor is 0.5 or $ \frac{1}{2} $ (half the size).
- Calculate the new dimensions: Multiplying each dimension by the scale factor gives us 4 inches by 6 inches.
- Transfer the measurements to drawing paper: Mark the new dimensions on a smaller sheet of paper and connect the dots to create the scaled-down outline.
Scaling Up a Drawing – Exercises
Scaling Drawings – Summary
Key Learnings from this Text:
- Scaling drawings requires a clear understanding of the scale factor concept.
- Consistency and accuracy in measurements are crucial for successful scaling.
- Utilization of grids can aid in maintaining proportional dimensions.
- Different mediums and techniques may be employed based on the required scale and context.
Ensure to review other resources on our platform for additional guidance on scaling drawings and related geometric concepts.
How to Create a Scale Drawing – Hands-On Activity
Here's an activity designed to help students understand scaling by enlarging a candy bar wrapper, a fun and practical application of the concepts discussed:
Scaling Up a Candy Bar Wrapper
Objective: Learn to scale up a drawing accurately using a ruler and grid technique. This activity helps students understand proportional relationships and apply scaling concepts practically.
Supplies Needed * A candy bar wrapper * A ruler * A pencil * Graph paper * Large drawing paper * Colored pencils or markers * A calculator (optional, for more precise calculations)
Scaling a drawing allows you to increase or decrease its size while keeping the proportions of the original image. In this activity, you will scale up a candy bar wrapper to understand how architects, artists, and designers work with different scale factors.
Step 1: Prepare Your Original Wrapper
- Measure the Dimensions: Use a ruler to measure the length and width of your candy bar wrapper. Write these measurements down.
Step 2: Determine the Scale Factor
- Choose a Scale Factor: Decide how much larger you want to make your wrapper. A good starting scale factor for this activity might be 2, 3, or 4. This means you will make the wrapper two, three, or four times larger than the original.
Step 3: Calculate the New Dimensions * Multiply the Original Dimensions: Use the scale factor to find the new dimensions. If your original wrapper is 3 inches by 5 inches and you choose a scale factor of 3:
- New length = original length × scale factor = 3 inches × 3 = 9 inches
- New width = original width × scale factor = 5 inches × 3 = 15 inches
Step 4: Draw a Grid on the Original Wrapper
- Draw a Grid: Using the graph paper, draw a grid over a photocopy or a clear sheet placed over your candy bar wrapper. Make each square in the grid equal to 1 square inch.
- Label the Grid: Number the rows and columns to keep track of each section.
Step 5: Transfer the Grid to Large Drawing Paper
- Draw a Larger Grid: On your large drawing paper, draw a grid that scales up from the original. If your scale factor is 3, each square on your new grid will be 3 inches.
- Use the Same Number of Squares: Ensure that the number of squares on the large grid matches the number of squares on the small grid, just at a larger scale.
Step 6: Copy the Wrapper
- Transfer the Image: Copy what is in each small square on your original wrapper to the corresponding large square on your new grid. This helps in maintaining the proportions and details accurately.
- Color: Once all details are transferred, use colored pencils or markers to color your scaled-up wrapper.
This activity not only teaches you how to scale drawings accurately but also allows you to appreciate the importance of maintaining proportions in design and visual arts.
Scaling Drawings – Frequently Asked Questions
Transcript How to Create a Scale Drawing
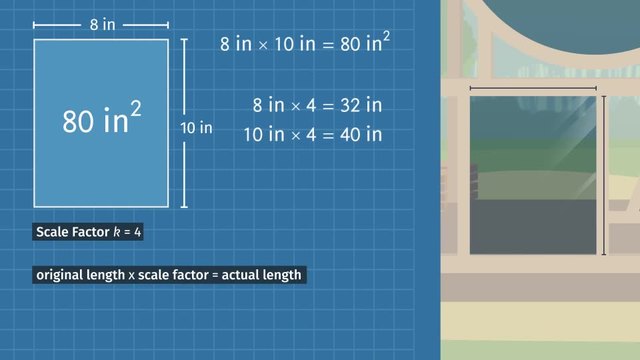
Alexey works in the busiest shipyard in all of Russia. He's an expert at organizing cargo of all shapes and sizes. A ship has just arrived at the docks. It has so much cargo that it is hard to tell if it can all fit in the yard! Alexey decides to create a scale drawing to help him figure out if he can fit all the cargo into the shipyard. The shipyard is 20 meters by 35 meters. To make a scale drawing, we first need to choose a scale factor. Remember, a scale factor is the ratio of any two corresponding side lengths of two similar geometric objects, like the scale drawing of the shipyard and the actual shipyard. Let's choose a scale factor of 2 centimeters in the drawing for every 5 meters in the actual shipyard. To rewrite our scale factor as a fraction, we always take the scale drawing as the numerator and the actual object as the denominator. We would like to use it to figure out how many centimeters in the drawing represents 20 meters in the actual shipyard and how many centimeters in the drawing represents 35 meters. Since we want the scale drawing and the actual shipyard to be proportional to each other, we would like these ratios to be equivalent ratios, meaning that they are all equal to each other. To find out how many centimeters represents 20 meters, we take the first two ratios and let our unknown be 'x', giving us the following equation. Cross-multiplying and solving for 'x', we find that 8 centimeters in the scale drawing represents 20 meters in the actual shipyard. Similarly, we take the last two ratios to figure out how many centimeters represents 35 meters. This gives us an equation. Cross-multiplying and solving for 'x', we get that 14 centimenters represents 35 meters in Alexey's scale drawing. So the dimensions of the shipyard in the drawing are 8 centimeters by 14 centimeters. Now Alexey is ready to pack in some cargo! Looks like the cargo consists of box crates, rectangular containers, and T-shaped cargo? First, the box crates. The crates are 7.5 meters wide and 7.5 meters long. As before, rewriting the scale factor as a fraction, we want to figure out how many centimeters in the scale drawing represents 7.5 meters. As we want the scale drawing of the box crates to be proportional to the actual box crates, we set these ratios equal to each other to indicate that they are equivalent ratios. Just as before, we have an equation. Cross-multiply and solve for our unknown to get that the square containers are 3 centimeters wide and 3 centimeters long in Alexey's scale drawing. It's time to place the box crates! Nice work, Alexey! Now Alexey needs to pack the rectangular containers into the shipyard. The containers are 10 meters long and 5 meters wide. How can we draw these containers? One length is covered, as we know from our scale factor that 2 centimeters represents 5 meters. We need to figure out how many centimeters represents 10 meters. We can set them equal to each other to get an equation. Cross-multiplying and solving for 'x', gives us 4 centimeters for every 10 meters. So each container will be 2 centimeters wide and 4 centimeters long. Whoa, that's a tight fit! Now for the T-shaped cargo.What is in these anyway? In real life, the actual sides of this cargo measure 2.5 meters, 5 meters, and 7.5 meters. How much space will these take up in Alexey's drawing? One length is covered, as we know from our scale factor that 5 meters is represented by 2 centimeters. We also know from our calculations with the box crates that 7.5 meters is represented by 3 centimeters. So all that is left is to find out how many centimeters represents 2.5 meters. Setting up an equation. Cross-multiplying and solving for 'x', gives us 1 centimeter for every 2.5 meters. As for arranging the cargo, they all just barely fit! Let's review our methods. First, choose the scale factor of our scale drawing. Then we note the actual measurements of the object we want to draw. Then we convert the actual measurements using our scale factor. We do this by setting up an equation of equivalent ratios, cross-multiplying, and solving for the unknown. Finally, we have what we need to create a scale drawing! After a hard day's work, Alexey can kick back and relax with his favorite video game. Hmm, looks like Alexey has a one-track mind!
How to Create a Scale Drawing exercise
-
Understand how to create a scale drawing.
HintsHere is an example of a scale factor: $10\:\text{ft}:1\:\text{in}$
A scale factor can be applied or used to solve problems involving two similar geometric objects.
When using a scale factor of a shape, we can compare two similar side lengths. These are called "corresponding sides".
SolutionThe ratio of any two corresponding side lengths of two similar geometric objects.
The scale factor is a special rule we use when comparing the sides of two similar shapes. It tells us how much bigger or smaller one side is compared to the same side on the other shape. It helps us understand how shapes are related to each other.
-
Identify a missing value given a scale factor.
HintsTo find the missing measurement, use cross-multiplication.
To cross-multiply, first multiply one numerator by the other denominator, and vice-versa. Next, you solve the one-step equation to find the value of the missing variable.
Solution$\frac{1\:\text{in}}{4\:\text{ft}} = \frac{3\:\text{in}}{\textbf{12\:\text{ft}}}$
$\frac{2\:\text{in}}{3\:\text{ft}} = \frac{\textbf{8\:\text{in}}}{12\:\text{ft}} $
$\frac{2\:\text{in}}{5\:\text{ft}} = \frac{6\:\text{in}}{\textbf{15\:\text{ft}}}$
$\frac{1\:\text{in}}{3\:\text{ft}} = \frac{\textbf{4\:\text{in}}}{12\:\text{ft}}$
-
Solve a proportion for a missing value.
HintsTo Cross-Multiply:
- Multiply each numerator by its opposite denominator and set those values equal to each other.
- Solve your one-step equation to arrive at a solution.
Remember you can always check your answer by substituting the solution in for the variable, and checking if it makes the equation true.
To check your solution, cross-multiply to confirm the equation is true.
Solution$\dfrac{2}{3}=\dfrac{n}{15}$
The first step is to cross-multiply.
$3(n)=2(15)$
$3n=30$
And then solve for the variable.
$\bf{n=10}$
-
Identify the measurements of a scale drawing.
HintsSteps to find the measurements of a scale drawing:
- Identify the scale factor
- Identify the actual measurements
- Convert
Here is an example where the scale factor is used to help find a measurement of the scale drawing. Be sure to match the units up when setting up a proportion.
SolutionThe scale factor of the actual pieces of cargo, to the scale drawing is: $2\:\text{cm}:5\:\text{m}$, and the measurements of the cargo are 10 m by 15 m.
Set up the first proportion.
$\dfrac{2\:\text{cm}}{5\:\text{m}}=\dfrac{x\:\text{cm}}{10\:\text{m}}$
Solve for x.
$x=4\:\text{cm}$
Set up the second proportion.
$\dfrac{2\:\text{cm}}{5\:\text{m}}=\dfrac{x\:\text{cm}}{15\:\text{m}}$
Solve for x.
$x=6\:\text{cm}$
The dimensions of the scale drawing of the piece of cargo are: $\bf{4\:\text{cm} \times 6\:\text{cm}}$
-
Determine a scale factor.
HintsA scale factor is a ratio. Ratios compare two quantities and can be written in three different ways:
$a\:\text{to}\:b$
$a:b$
$\dfrac{a}{b}$
The scale factor of $5\:\text{cm}:9\:\text{m}$ can be rewritten as $\frac{5\:\text{cm}}{9\:\text{m}}$.
SolutionA scale factor is a ratio. Ratios compare two quantities and can be written in three different ways:
$a\:\text{to}\:b$
$a:b$
$\dfrac{a}{b}$
$3\:\text{feet}:7\:\text{miles}=\mathbf{\dfrac{3\:\text{ft}}{7\:\text{mi}}}$
-
Calculate the dimensions of a scale drawing given a scale factor.
HintsFollow these steps from the video to create a scale drawing.
To convert the actual measurements using a scale factor, set up a proportion and solve for the missing values.
Notice here, a proportion is set up to find the height of a scale drawing of the actual building.
$\dfrac{2\:\text{in}}{25\:\text{ft}}=\dfrac{x}{200\:\text{ft}}$
SolutionTo find the scale drawing length for $10\:\text{ft}$, this proportion will be set up and then solved for $x$.
$\dfrac{1\:\text{in}}{5\:\text{ft}}=\dfrac{x\:\text{in}}{10\:\text{ft}}$
$x = \bf{2\:\text{in}}$
To find the scale drawing length for $25\:\text{ft}$, this proportion will be set up and then solved for $y$.
$\dfrac{1\:\text{in}}{5\:\text{ft}}=\dfrac{y\:\text{in}}{25\:\text{ft}}$
$y = \bf{5\:\text{inches}}$