Surface Area of Simple 3D Shapes


Basics on the topic Surface Area of Simple 3D Shapes
After this lesson, you will be able to construct nets from given 3D solids to find surface areas.
The lesson begins by teaching the definition of surface area. It leads to calculating the surface area of a rectangular prism using nets and the formula, SA=2lw+2wh+2lh. It concludes with calculating surface areas of triangular prisms and cylinders using the formula, SA=2Abase+ph.
Learn how to calculate surface areas by figuring out how much paint the Mad Hatter needs to cover the Queen’s throne.
This video includes key concepts, notation, and vocabulary such as 3D figures (a closed 3D geometric object), rectangular or triangular prisms (two congruent rectangular or triangular bases connected with rectangular lateral faces), bases (the two congruent opposite faces that define a prism), lateral faces (the remaining rectangular faces that connect the bases), faces (the 2D polygons of which prisms and pyramids are made), edges (the segments connecting the faces), vertices (the points where edges meet), and the surface area formula SA=2Abase+ph, where Abase represents the area of the base of the prism, p represents perimeter, h represents height.
Before watching this video, you should already be familiar with constructing 3D figures from nets, 3D solids (specifically pyramids and prisms), and finding the area of rectangles and triangles.
After watching this video, you will be prepared to learn find the surface area for multiple types of prisms.
Common Core Standard(s) in focus: 6.G.A.2, 6.G.A.4 A video intended for math students in the 6th grade Recommended for students who are 11 - 12 years old
Transcript Surface Area of Simple 3D Shapes
On what should be a happy night in Wonderland the queen is throwing one of her famous tantrums. She just got a new throne delivered and it's NOT red! The queen summons the Mad Hatter to fix the problem immediately. How much paint will the Mad Hatter need to cover the throne? To answer this question, we'll need to calculate the surface area of simple 3D shapes. Surface area is the sum of the areas of all the surfaces of a shape. The queen's throne is a COMPOSITE of SEVERAL shapes. What shapes do you see? We have a rectangular prism here a triangular prism here and four cylindrical legs. Let's look at the rectangular prism first. This prism is 25 inches...by 22 inches...by 4 inches. The top and bottom faces are rectangles with dimensions 25 by 22. So the area of one of these faces is length times width, or 550 square inches. That makes their combined area twice that, or 1100 square inches. The FRONT face is 22 by 4 so the area is 88 square inches. The BACK face is identical so that's 176 square inches for both of these sides combined. The LEFT face is 25 by 4 so the area is 100 square inches. With the identical right face, that makes 200 square inches combined. Adding all these areas together gives us a surface area of 1,476 square inches. In general, we can find the surface area of a rectangular prism with this formula 2 times length times width, plus 2 times width times height, plus 2 times length times height. The majestic back of the throne is a TRIANGULAR prism. The FRONT and BACK faces of this shape are ISOSCELES TRIANGLES, with LEGS of 39 inches and BASE of 30 inches. This triangle has a HEIGHT of 36 inches. The area of a TRIANGLE is one-half of the base times the height. That's half of 30 times 36 which is 15 times 36, or 540. Because there is an identical triangle on the BACK...we double that to get 1,080 square inches. Now to calculate the LATERAL AREA of this shape, or the area of all the remaining faces combined. To do that, imagine placing the prism so that one triangular face is on the ground. Now, unfolding the sides gives us one long rectangle, with a height of 3 inches. The length of this long rectangle is the same as the PERIMETER of our triangle, or the length of all three sides combined. The AREA of this long rectangle can be found by multiplying the length, 108 inches, times the height, 3 inches...which gives us 324 square inches. We add the area of the triangles and the area of the lateral faces to get a surface area of 1,404 square inches. In general, we can find the surface area of any prism in two steps. First, find the area of the BASE of the prism and double it. Then, find the PERIMETER of the base and multiply it times the height to get the LATERAL area of all the sides combined. Add those together and we've got the surface area of the prism. We can use this idea to find the surface area of the four cylinders that compose the legs of the queen's chair, as well. The height of each cylinder is 15 inches. The circular bases of each cylinder have a radius of 2 inches. So what does that make the area of one circular base? Using the area formula for a circle pi times the radius 2 squared gives us an area of 4 pi for each base. We double that to get a combined area of 8 pi for the top and bottom. Now, how would you calculate the area of the lateral face? If we unroll the lateral face, we can see that it's a rectangle with a height of 15 inches. But what's the length? The length of the lateral face is the same as the CIRCUMFERENCE of the circular BASE. Do you remember how to find the circumference of a circle? That's 2 pi times the radius, 2, or 4 pi. So the lateral area is 4 pi times 15, or 60 pi. Adding the faces together, that gives us a surface area of 68 pi per cylinder. Now, to find the total surface area of the throne, we add all our parts together. 1,476 square inches for the rectangular prism plus 1,404 square inches for the triangular prism plus 4 times the surface area of one cylindrical prism, since we have four legs. Using 3.14 as an approximation for pi that gives us a TOTAL surface area of about 3,734.08 square inches. To review, we can find the surface area of prisms and cylinders in just a few steps. First, find the area of the BASE, and double it. That might mean finding the area of a rectangle a triangle or a circle. Then, find the perimeter or circumference of the base. Multiply the perimeter or circumference times the height to find the lateral area. Add the area of the bases and the lateral area to get the total surface area. By calculating the total surface area, the Mad Hatter was able to use just the right amount of paint on the throne. It looks perfect, but wait a second, Your Highness! Oh no... Now the queen is definitely seeing red.
Surface Area of Simple 3D Shapes exercise
-
Find the surface area of each prism.
HintsThe area of the top and bottom of the rectangular prism is,
- $\text{Area}=2(16\cdot 12)~\text{in}^2$
- $\text{Area}=2(192)~\text{in}^2$
- $\text{Area}=384~\text{in}^2$
The perimeter, $P$, of an isosceles triangle with leg lengths $15~\text{in}$ and base $10~\text{in}$ is,
- $P=15~\text{in}+15~\text{in}+10~\text{in}$
- $P=40~\text{in}$
The area for the circular bases of the cylinder is,
- $A=2(\pi \cdot 3^2)~\text{in}^2$
- $A=18\pi ~\text{in}^2$
- $A\approx18(3.14)~\text{in}^2$
- $A\approx56.52~\text{in}^2$
SolutionRectangular Prism
To find the area of the rectangular prism, use the following steps:
1. Recall that the area of a rectangle is found by multiplying the length by the width.
2. Find the area of the following faces:
- Let length $l=22$, width $w=19$, and height $h=6$.
- Top: $A=lw=22~\text{in}\cdot 19~\text{in}=418~\text{in}^2$
- The areas for the top and bottom of the rectangular prism are the same. So, we can just multiply the area of the top by $2$ to get the area of both the top and bottom. Now we can find the area of the six faces.
- Top & Bottom: $A=2(lw)=2(22~\text{in}\cdot 19~\text{in})=2(418)~\text{in}^2=836~\text{in}^2$
- Front & Back: $A=2(wh)=2(19~\text{in}\cdot 6~\text{in})=2(114)~\text{in}^2=228~\text{in}^2$
- Left & Right:$A=2(lh)=2(22~\text{in}\cdot 6~\text{in})=2(132)~\text{in}^2=264~\text{in}^2$
- $\text{Surface Area}=836~\text{in}^2+228~\text{in}^2+264~\text{in}^2$
- $\text{Surface Area}=1,328~\text{in}^2$
$~$
Triangular Prism
To find the area of the triangular prism, use the following steps:
1. Recall that the area of a triangle is found by multiplying the base and height by $\frac{1}{2}$.
2. Find the area of the front and back triangles:
- Use the area of a triangle formula, $\frac{1}{2}bh$, and multiply it by $2$ to represent both the front and back.
- Let base $b=23$, height $h=29$.
- Front & Back:$A=2(\frac{1}{2}bh)=2(\frac{1}{2}\cdot 23~\text{in}\cdot 29~\text{in})=2(333.5)~\text{in}^2=667~\text{in}^2$
- Lateral Face: $A=hP=2~\text{in}(31~\text{in}+31~\text{in}+23~\text{in})=170~\text{in}^2$
- $\text{Surface Area}=667~\text{in}^2+170~\text{in}^2=837~\text{in}^2$
$~$
Cylinder
To find the area of the cylinder, use the following steps:
1. Recall that the area of a circle is found by using the formula $A=\pi r^2$.
2. Find the area of the two circular bases:
- Use the area of a circle formula and multiply it by $2$ to represent both bases.
- Bases: $A=2(\pi \cdot 4^2)~\text{in}^2=2(16\pi)~\text{in}^2=32\pi~\text{in}^2$
- Base:$C=2\pi \cdot 4~\text{in}=8\pi ~\text{in}$
- Lateral Face: $A=16~\text{in}(8\pi ~\text{in})=128\pi~\text{in}^2$
- $\text{Surface Area}\approx 32(3.14)~\text{in}^2+128(3.14)~\text{in}^2\approx 100.48~\text{in}^2+401.92~\text{in}^2=502.4~\text{in}^2$
-
Identify the formula for the surface area of each prism.
HintsThe surface area for all prisms can be found by doubling the area of the base and adding the lateral area.
The area of the base can be found by identifying the shape, and using the area formula for that particular shape.
The base of a cylinder is a circle.
SolutionThe surface area for all prisms can be found by doubling the area of the base, the shape that clarifies the 3D object, and adding the lateral area.
This is represented by the formula, $SA=2A_{\text{base}}+Ph$, where $P$ is the perimeter of the lateral face, and $h$ is the height of the lateral face.
1. The formula for the surface area of a cylinder is, $SA=2(\pi r^2)+Ph$.
- The base of a cylinder is a circle.
- The area of a circle is, $A=\pi r^2$.
- The lateral face is a rectangle represented by $Ph$, where $P$ is actually the circumference of the circular base, $C=2 \pi r$, and $h$ is the height of the cylinder.
- The base of a rectangular prism is a rectangle.
- The area of a rectangle is $A=lw$
- There are four lateral faces that are all rectangles: the front, back, left, and right of the prism, which represent $2wh$ and $2lh$.
- The base of a triangular prism are two triangles.
- The area of a triangle is $A=\frac{1}{2}bh$, where $b$ represents the base, and $h$ represents the height.
- The lateral face is a rectangle formed from unfolding the sides and is represented by $Ph$, where $P$ is the perimeter of all $3$ sides, and $h$ is the height of the unfolded side.
- The base of a cylinder is a circle.
- The area of a circle is, $A=\pi r^2$.
- $3.14$ is used an approximation for $\pi$.
- The lateral face is a rectangle represented by $Ph$, where $P$ is the circumference of the circular base and $h$ is the height of the cylinder.
-
Determine the surface area of each prism.
Hints$3.14$ can be used as an approximation for pi, $\pi$.
The surface area of the cylinder is found by solving the following expression,
- $SA \approx 2(\pi\cdot 2^2)~\text{in}^2+(2\pi \cdot 2)(10)~\text{in}^2$
The surface area of the triangular prism is found by solving the following expression,
- $SA=2\left( \frac{1}{2}(16\cdot 15)~\text{in}^2 \right)+(16+17+17)(1)~\text{in}^2$
Solution1. Cylinder with radius $7~\text{in}$ and height $17~\text{in}$.
- The surface area is found by using the formula, $SA=2\text{Area}_{\text{circle}}+Ph$.
- $Ph$ represents the lateral face of the cylinder found by unrolling the face of the cylinder into a rectangle.
- The rectangle is composed of the circumference, which we use the perimeter, $P$, of the circular base, and the height $h$ of the cylinder.
- The area of a circle is $\pi r^2$, and the circumference of a circle is $2\pi r$.
- $SA=2(\pi \cdot 7^2)+(2\pi \cdot 7)\cdot 17$
- $SA \approx 2(3.14\cdot 49)+(2\cdot 3.14\cdot 7)\cdot 17$
- $SA \approx 307.72+747.32$
- $SA \approx 1,055.04~\text{in}^2$
- The surface area is found by using the formula, $SA=2\text{Area}_{\text{triangle}}+Ph$.
- $Ph$ represents the lateral faces of the prism found by placing 1 triangular face on ground and unfolding the sides into 1 long rectangle.
- The rectangle is composed of the perimeter $P$ of the isosceles triangle, and the depth $h$ of the triangular prism.
- $SA=2\cdot \frac{1}{2}(18\cdot 12)+(15+15+18)(3)$
- $SA=216+144$
- $SA=360~\text{in}^2$
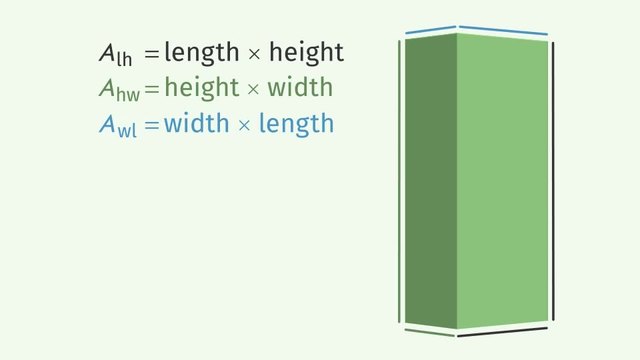
- The surface area is found by using the formula, $SA=2lw+2wh+2lh$, where $l$ represents the length, $w$ represents the width, and $h$ represents the height.
- The surface area is basically adding the areas of all 6 rectangular faces: front, back, top, bottom, left and right.
- $SA=2(21\cdot 12)+2(12\cdot 17)+2(21\cdot 17)$
- $SA=2(252)+2(204)+2(357)$
- $SA=504+408+714$
- $SA=1,626~\text{in}^2$
- The surface area is found by using the formula, $SA=2\text{Area}_{\text{circle}}+ph$.
- $Ph$ represents the lateral face of the cylinder found by unrolling the face of the cylinder into a rectangle.
- The rectangle is composed of the circumference, which we use the perimeter, $P$, of the circular base, and the height $h$ of the cylinder.
- The area of a circle is $\pi r^2$ and the circumference of a circle is $2\pi r$.
- $SA=2(\pi \cdot 5^2)+(2\pi \cdot 5)\cdot 10$
- $SA \approx 2(3.14\cdot 25)+(2\cdot 3.14\cdot 5)\cdot 10$
- $SA=157+314$
- $SA=471~\text{in}^2$
- The surface area is found by using the formula, $SA=2\text{Area}_{\text{triangle}}+Ph$.
- $Ph$ represents the lateral faces of the prism found by unfolding the sides into 1 long rectangle.
- The rectangle is composed of the perimeter $P$ of the isosceles triangle, and the depth $h$ of the triangular prism.
- $SA=2\cdot \frac{1}{2}(10\cdot 12)+(13+13+10)(2)$
- $SA=120+72$
- $SA=192~\text{in}^2$
-
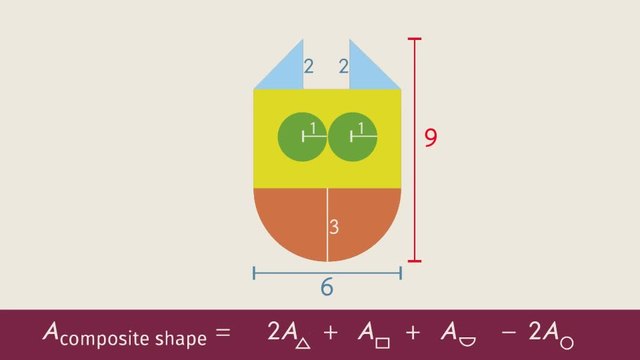
Calculate the surface area of the given composite 3D object.
HintsThe surface area for all prisms can be found by doubling the area of the base and adding the lateral area.
Remember that the radius of a circle is half the diameter.
The total surface area is represented by four cylinders, one triangular prism, and one rectangular prism. Don't forget to subtract the area of any shared sides that are not on the surface.
SolutionTo find the surface area of the 3D figure, we need to calculate the surface of the individual prisms and cylinders, then add them all together. There are 4 cylinders, 1 triangular prism, and 1 rectangular prism.
1. Find the surface area of the 4 cylinders with diameter $2~\text{in}$ and height $5~\text{in}$.
- The surface area is found by using the formula, $SA=2(\pi r^2)+Ph$.
- $Ph$ represents the lateral face of the cylinder found by unrolling the face of the cylinder into a rectangle.
- The rectangle is composed of the circumference $P$ of the circular base, and the height $h$ of the cylinder.
- The area of a circle is $\pi r^2$ and the circumference of a circle is $2\pi r$.
- Since the diameter is twice the radius, we know that $r=1~\text{in}$.
- $SA=2(\pi \cdot 1^2)~\text{in}^2+(2\pi \cdot 1)\cdot 5~\text{in}^2$
- $SA\approx 2(3.14\cdot 1)~\text{in}^2+(2\cdot 3.14\cdot 1)\cdot 5~\text{in}^2$
- $SA\approx 6.28~\text{in}^2+31.4~\text{in}^2$
- $SA\approx 37.68~\text{in}^2$
- The surface area of 1 cylinder is $37.68~\text{in}^2$, which makes the surface area of 4 cylinders, $4(37.68~\text{in}^2)=150.72~\text{in}^2$.
- Since the top and bottom of all four cylinders are being shared with the other objects and therefore not on the surface, subtract the area of $8$ circles from the total surface area.
- $\text{Area}=8\pi r^2=8(\pi \cdot (1~\text{in})^2)=8\pi~\text{in}^2\approx 8(3.14)~\text{in}^2\approx 25.12~\text{in}^2$.
- The new surface area is $150.72~\text{in}^2-25.12~\text{in}^2=125.60~\text{in}^2$.
- The surface area is found by using the formula, $SA=2(\frac{1}{2}bh_{1})+Ph_{2}$.
- $Ph_{2}$ represents the lateral faces of the prism, found by placing 1 triangular face on ground and unfolding the sides into 1 long rectangle.
- The rectangle is composed of the perimeter $P$ of the isosceles triangle, and the depth $h_{2}$ of the triangular prism.
- $SA=2\cdot \frac{1}{2}(10\cdot 12)~\text{in}^2+(13+13+10)(3)~\text{in}^2$
- $SA=120~\text{in}^2+36(3)~\text{in}^2$
- $SA=120~\text{in}^2+108~\text{in}^2$
- $SA=228~\text{in}^2$
- The surface area is found by using the formula, $SA=2lw+2wh+2lh$, where $l$ represents the length, $w$ represents the width, and $h$ represents the height.
- The surface area is basically adding the areas of all 6 rectangular faces: front, back, top, bottom, left and right.
- $SA=2(10\cdot 3)~\text{in}^2+2(3\cdot 4)~\text{in}^2+2(10\cdot 4)~\text{in}^2$
- $SA=2(30)~\text{in}^2+2(12)~\text{in}^2+2(40)~\text{in}^2$
- $SA=60~\text{in}^2+24~\text{in}^2+80~\text{in}^2$
- $SA=164~\text{in}^2$
- $SA=125.60~\text{in}^2+228~\text{in}^2+164~\text{in}^2$
- $SA=517.60~\text{in}^2$
-
Compute the area of each shape.
Hints$3.14$ can be used as an approximation for pi, $\pi$.
The radius, $r$, is a straight line from the center to the circumference of a circle.
The area for a triangle with a base of $4~\text{in}$ and height of $8~\text{in}$, is $16~\text{in}^2$.
SolutionGreen Circle
- The area formula for a circle is $A=\pi r^2$, where $r$ represents the radius.
- The image shows that the radius is $3~\text{in}$.
- $\text{A}=\pi (3^2)~\text{in}^2$
- $\text{A}\approx 3.14(9)~\text{in}^2$
- $\text{A}\approx 28.26~\text{in}^2$
- The area formula for a triangle is $A=\frac{1}{2}bh$, where $b$ represents the base and $h$ represents the height.
- The image shows that the base is $6~\text{in}$ and the height is $4~\text{in}$.
- $\text{A}=\frac{1}{2}(6)(4)~\text{in}^2$
- $\text{A}=3(4)~\text{in}^2$
- $\text{A}=12~\text{in}^2$
- The area formula for a rectangle is $A=lw$, where $l$ represents the length and $w$ represents the width.
- The image shows that the length is $10~\text{in}$ and the width is $6~\text{in}$.
- $\text{A}=10(6)~\text{in}^2$
- $\text{A}=60~\text{in}^2$
-
Find the surface area of the composite 3D object.
HintsThe surface area for all prisms can be found by doubling the area of the base and adding the lateral area.
Unraveling the lateral faces of a prism normally creates a rectangular figure.
The total surface area of the 3D figure is represented by a rectangular prism and a triangular prism. Don't forget to subtract the area of any shared sides that are not on the surface.
SolutionTo find the surface area of the 3D figure, we need to calculate the surface of the individual prisms, then add them all together, and subtract the area of any sides that are not on the surface. There is 1 triangular prism and 1 rectangular prism.
1. Find the surface area of the rectangular prism length $8~\text{cm}$, width $10~\text{cm}$, and height $4~\text{cm}$.
- The surface area is found by using the formula, $SA=2lw+2wh+2lh$, where $l$ represents the length, $w$ represents the width, and $h$ represents the height.
- The surface area is basically adding the areas of all 6 rectangular faces: front, back, top, bottom, left and right.
- $SA=2(8\cdot 10)~\text{cm}^2+2(10\cdot 4)~\text{cm}^2+2(8\cdot 4)~\text{cm}^2$
- $SA=2(80)~\text{cm}^2+2(40)~\text{cm}^2+2(32)~\text{cm}^2$
- $SA=160~\text{cm}^2+80~\text{cm}^2+64~\text{cm}^2$
- $SA=304~\text{cm}^2$
- Since the top of the rectangular prism is a shared side and not on the surface, subtract the rectangular area from the total surface area.
- $\text{Area}=8~\text{cm}\cdot 10~\text{cm}=80~\text{cm}^2$
- The new surface area is $304~\text{cm}^2-80~\text{cm}^2=224~\text{cm}^2$.
- The surface area is found by using the formula, $SA=2(\frac{1}{2}bh_{1})+Ph_{2}$.
- $Ph_{2}$ represents the lateral faces of the prism, found by placing 1 triangular face on ground and unfolding the sides into 1 long rectangle.
- The rectangle is composed of the perimeter $P$ of the isosceles triangle, and the depth $h_{2}$ of the triangular prism.
- $SA=2\cdot \frac{1}{2}(8\cdot 3)~\text{cm}^2+(5+5+8)(10)~\text{cm}^2$
- $SA=24~\text{cm}^2+18(10)~\text{cm}^2$
- $SA=24~\text{cm}^2+180~\text{cm}^2$
- $SA=204~\text{cm}^2$
- Since the bottom of the triangular prism is a shared side and not on the surface, subtract the rectangular area from the total surface area.
- $A=8~\text{cm}\cdot 10~\text{cm}=80~\text{cm}^2$
- The new surface area is $204~\text{cm}^2-80~\text{cm}^2=124~\text{cm}^2$.
- $SA= 224~\text{cm}^2+124~\text{cm}^2$
- $SA=348~\text{cm}^2$