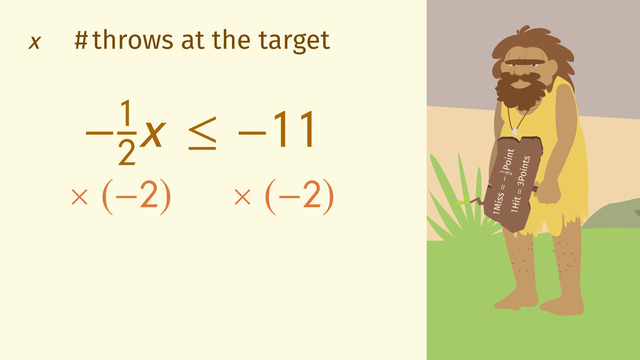Solving Two-Step Inequalities


Basics on the topic Solving Two-Step Inequalities
Just like equations, inequality problems can require two-steps to calculate the solution. To solve, just like a two-step equality, use the Distributive Property to eliminate any parentheses.
Now Step 1: use the opposite operations of addition or subtraction to isolate the variable from the constant.
Step 2: use the opposite operations of multiplication or addition to isolate the variable from the coefficient. Remember to keep the inequality balanced, whatever you do to one side of the inequality sign you must do to the other.
Now, different from equations, you must consider the direction of the sign. If you multiplied or divided by a positive number, maintain the sign but if you multiply or divide by a negative number, you must flip the sign over so it points in the opposite direction.
Plotting the inequality on a number line lets you see the all the possible solutions. Use common sense, is a negative value reasonable for the problem you are solving? If not, determine that the least possible solution is zero, and indicate this in your answer. Remember an open dot is used to represent solutions that are less than or greater than, and a closed dot is used for solutions that are greater than and equal to or less than and equal to.
Use inequalities to solve problems. CCSS.MATH.CONTENT.HSA.CED.A.3
Transcript Solving Two-Step Inequalities
Miss Crazycat is sitting in her living room reading a letter she received from the City Council today. She is shocked! There is a new law: a maximum of 10 cats are allowed per household.
Miss Crazycat doesn't even know how many cats she has... and it's not exactly easy to count them as they are running around all the time.
But she does know how many cans of fish they eat. So she wants to use math by solving two-step inequalities.
Example of a two-step Inequality
All her cats together eat 50 cans of fish in 5 days. Every cat eats at least one can of fish per day. We are looking for Miss Crazycat's total number of cats.
Since you don't know the number of cats yet let's call it x. But wait, Miss Crazycat just remembered, two of her cats are vegetarian. So the number of fish-eating cats is x - 2.
Let's summarize what we know. The fish-eating cats can be represented as x - 2. In 5 days they eat 50 cans of fish. Since Miss Crazycat knows that each cat eats at least one can of fish each day, you have to put a less than or equal to sign in between the two expressions.
Solving a two-step Inequality
So let's calculate. We start with the Distributive Property here to eliminate the paratheses. You multiply x by 5 which is 5 x, and you multiply negative 2 by 5, which equals negative 10.
Now you use opposite operations to isolate your unknown number x. Remember to do this with PEMDAS reversed. The opposite of subtraction is addition, so we add 10 to the left side of the equation. What we do to one side, we must do to the other side: We add another 10 to the right side: 5x − 10 + 10 = 5x.
And 50 + 10 = 60. Remember, the less than or equal to sign stays the same unless multiplying or dividing by a negative number.
The opposite of multiplication is division, so you divide both sides by 5. The final answer is x ≤ 12. So we have 2 vegetarian cats and 10 or less fish-eating cats.
Solutions on a Number Line
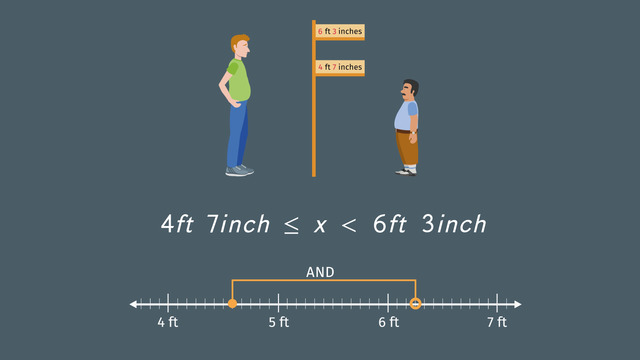
Let's show all of the possible solutions using a number line. The total number of cats is 12 or less. So it should look like this.
But Miss Crazycat can't have a negative number of cats, so the least possible solution is 0. Now we also know that she has two vegetarian cats. She also has to have at least one fish-eating cat because somebody has to be eating the fish! So she has at least 3 cats but no more than 12.
Miss Crazycat can't be certain that she is obeying the City Council's 10 cat limit. So just to be sure, she disguises two of the cats.
Solving Two-Step Inequalities exercise
-
Determine how Miss. Crazycat can estimate the number of cats.
HintsLet's assume that Miss Crazycat owns $15$ cats. $13$ cats eat fish.
Pay attention to the rules of PEMDAS:
- Evaluating parentheses first:
- You get the same result by using the Distributive Property:
- $5x=60$ is an equality
- $5x<60$, $5x\le60$, $5x>60$ and $5x\ge 60$ are inequalities
SolutionLet's try to help Miss Crazycat solve her problem, by estimating how many cats she has living in her home.
First of all, we assign the unknown number of cats to the variable $x$. Because two cats are vegetarian, there are $x-2$ cats that eat fish. We know that fewer than $50$ cans of fish will be eaten in $5$ days. Writing this mathematically, we get the inequality $(x-2)\times 5\le 50$.
Using the Distributive Property, we multiply the contents of the parentheses by $5$. Doing this leaves us with $5x-10\le 50$.
We perform the opposite operation of $-10$ on both sides, which gives us $5x\le 60$.
Last but not least, we divide by $5$. We have to pay attention to the sign of $5$. It's positive, so the sign $\le$ stays the same: $x\le 12$.
So, now Miss Crazycat knows that the number of cats in her apartment is less than or equal to $12$.
-
Estimate the number of cats in Miss. Crazycat's apartment.
HintsThe inequality we need to solve is $(x-2)\times 5\le 50$.
This leads to $x\le 12$.
Miss Crazycat knows that two of her cats are vegetarians.
Miss Crazycat's cats eat $50$ cans of fish in $5$ days. Let's assume that neither Miss Crazycat nor the two vegetarian cats eat any cans of fish. So, there has to be at least one cat that eats fish.
A negative number of cats is not possible. Poor $-1$ cat!
SolutionLet's look at the given information:
- We assign the unknown number of cats to the variable $x$.
- Miss Crazycat has two vegetarian cats, so $x-2$ represents the number of cats that eat fish.
- Her cats eat $50$ cans of fish in $5$ days.
Now we have two vegetarian cats and at least one fish-eating cat, so Miss Crazycat has at least $3$ cats.
We can conclude that Miss Crazycat has between $3$ and $12$ cats. We can express this mathematically as $3\le x\le 12$.
Unfortunately, Miss Crazycat still doesn't know if she has fewer than $10$ cats...
-
Write an inequality to describe a number line.
HintsFirst, transform each inequality to a simpler version.
$\begin{array}{lcl} x+5&\le&15\\ ~~~\color{#669900}{-5}&&\color{#669900}{-5}\\ x&\le& 10 \end{array}$
You can draw the graph of $x\le10$ by drawing a closed circle at $10$ and an arrow pointing to the left.
You can draw the graph of $x \ge 10$ by drawing a closed circle at $10$ and an arrow pointing to the left.
SolutionDrawing graphs of inequalities is a good way to help you understand their solution sets.
- For the inequality $x+2\le8$, subtracting $2$ from both sides gives us $x\le 6$. You can draw the graph of $x+2\le8$ by drawing a closed circle at $6$ and an arrow pointing to the left.
- For the inequality $x-2\ge4$, adding $2$ to both sides gives us $x\ge 6$. You can draw the graph of $x\ge6$ by drawing a closed circle at $6$ and an arrow pointing to the right.
- For the inequality $x+4\ge 11$, subtracting $4$ from both sides gives us $x\ge 7$. You can draw the graph of $x\ge7$ by drawing a closed circle at $7$ and an arrow pointing to the right.
- For the inequality $x+6\le 13$, subtracting $6$ from both sides gives us $x\le 7$. You can draw the graph of $x\le7$ by drawing a closed circle at $7$ and an arrow pointing to the left.
-
Describe how Miss. Crazydog can estimate the number of dogs living in her home.
HintsIt's a good idea to check your solution. The total number of cans of normal dog food eaten by Miss Crazydog's dogs should be $56$.
Use Opposite Operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
SolutionIt's not raining cats and dogs, but nevertheless Miss Crazycat and her friend Miss Crazydog have the same problem. They've lost count of how many cats or dogs they have living in their homes.
Miss Crazydog knows that all but one of her dogs eat $2$ cans of dog food everyday, and one of her dogs is a vegetarian, so this dog does not eat canned dog food. Her dogs eat $56$ cans in total.
$x$ is the number of dogs, and $x-1$ the number of non-vegetarian dogs.
This gives us the equation $(x-1)\times 2\times7=(x-1)\times 14=56$.
First, we use the Distributive Property to get
$14x-14=56$
Now we add $14$ on both sides of the equation sign, leaving us with:
$14x=70$
Finally, by dividing by $14$ on both sides of the equation, we get the solution:
$x=5$
Miss Crazydog has $5$ dogs in total, $1$ vegetarian dog, and $4$ meat eaters.
Let's check and see if this solution is correct: $4$ dogs eating $2$ cans each of seven days leads to $4\times 2\times 7=56$. That's correct!
-
Describe the meaning of the inequality sign $\le$.
Hints$\le$ means less than OR equal to.
$<$ means less than.
There's a difference between less than and at most as well as between more than and at least.
SolutionThe number of Miss Crazycat's cats can be expressed using the inequality $x\le 12$.
What does this mean? The number of cats is, at most, $12$.
- Less than $12$ is written as $x<12$.
- More than $12$ is written as $x>12$.
- At least $12$ is written as $x\ge 12$.
- Equal to $12$ is written as $x=12$.
-
Solve the following inequalities.
HintsUse Opposite Operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
You can solve an inequality in a manner similar to solving equalities. But keep in mind that multiplying or dividing by a negative number flips the sign. For example:
$2<x$ but $-2>-x$
You can solve each inequality in two steps.
The sign of only one inequality flips.
SolutionHow do you solve a two-step inequality? The process is similar to solving two-step equations, but in order to isolate the variable in an inequality, we have to pay special attention when we multiply or divide by negative numbers. In these special cases, we have to flip the inequality sign.
Take a look at this example:
$2<3$ is obviously true. If we multiply by $-2$ we get $-4$ on the left an $-6$ on the right side. So the inequality $-4>-6$ is valid. Notice how we flipped the sign?
$\begin{array}{rclcl} 2x+4&<& ~10\\ \color{#669900}{-4}&&\color{#669900}{-4}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 2x&< &~~~6\\ \color{#669900}{\div2}&&\color{#669900}{\div2}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&<& ~~~3 \end{array}$
It works the same for the following equations:
$\begin{align*} 3(x+1)&< 15\\ x+1&< 5\\ x&< 4 \end{align*}$
... and ...
$\begin{align*} 3x+1&< 19\\ 3x&< 18\\ x&< 6 \end{align*}$
Let's take a closer look at an inequality where the sign flips:
$\begin{array}{rcrcl} -2x+8&<& 14~~\\ \color{#669900}{-8}&&\color{#669900}{-8}~~&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ -2x&<& 6~~\\ \color{#669900}{\div(-2)}&&\color{#669900}{\div(-2)}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&>& -3~~&&|\text{ Flip the Sign!} \end{array}$