Solving Two-Step Equations
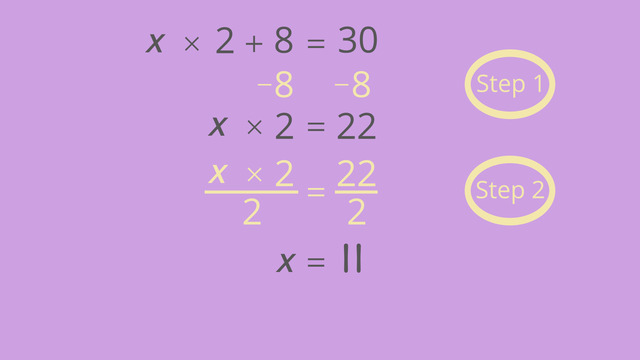

Basics on the topic Solving Two-Step Equations
When solving algebraic two-step equations, like one-step equations, your goal is to isolate the variable on one side of the equal sign, but for two-step equations, you will need to do an extra step, hence the name, two-step equations.
To solve two-step equations, the first step is to simplify the variable equation by using addition or subtraction. If a number is added or subtracted with the variable, do the opposite or inverse operation on both sides of the equal sign. Next is the second step, to isolate the variable that is multiplied or divided with a number, use the inverse operation on both sides of the equal sign and you will have solved for the variable.
For the equation 2x + 5 = 9, step one is to subtract 5 from both sides of the equation, leaving 2x = 4. Step two is to divide by 2 on both sides of the equation, leaving x = 2. By following the two steps, it’s easy to solve algebraic equations.
Just remember, to isolate the variable the first step is to add or subtract, and the second step is to multiply or divide. Don’t forget, the inverse of addition is subtraction, and the inverse of multiplication is division and remember, to keep the equation balanced, whatever you do to one side of the equation, you must do to the other.
Explain steps to solve algebraic equations. CCSS.MATH.CONTENT.HSA.REI.A.1
Transcript Solving Two-Step Equations
Shannon is at a concert watching her favorite band play. Of course, she wants to snag some photos and videos during the concert.
An example problem for two-step equations
Oh no! Her battery is low!!! Shannon has to save as much battery as possible. She knows that her favorite song is playing at the end of the concert, and she wants to film it, no matter what.
Taking the video of the last song will cost her 8% of her remaining 30% battery life. Every photo taken will cost Shannon an additional 2%.
So, how many photos can Shannon take during the concert, with having enough battery left for the video of the last song? We can solve this using an equation.
The battery must last long enough to take one video and some photos. Since you are trying to find out how many photos Shannon can take, let x represent the number of photos taken during the concert.
Okay, we said taking a photo will cost 2%, so you can put 2% in place of the photo symbol. Also, replace the video symbol with 8% because the video will use up 8%. Finally, replace the battery symbol with 30% because Shannon has 30% battery life left.
Solving two-step Equations Step 1
Now we have the equation x · 2 + 8 = 30. Let's solve this equation for x to find out how many photos Shannon can take during the concert.
Equations like this can be solved in two steps. Your first step is to simplify by addition or subtraction. Because 8 is added in the problem, you need to use the inverse operation, subtraction, to solve.
Subtract 8 from both sides of the equals sign. The positive 8 minus 8 cancels out to be zero. So you get x · 2 = 22.
Solving two-step Equations Step 2
The second step is to isolate the variable by multiplication or division. In the problem, x is being multiplied by two. The inverse of multiplication is division, so you should divide both sides of the equation by 2.
x · 2 ÷ 2 reduces to 1x or x on the left. 22 ÷ 2 = 11. So x = 11. Remeber, x represents the number of photos Shannon can take during the concert. This means Shannon can take 11 photos plus one video before her phone dies.
We can solve all equations that look like this one using just two steps:
- In the first step, you will always add or subtract.
- Then, in the second step, you will multiply or divide.
It would be a pity if she couldn't record this awesome song! Oh no! It can't be true! She's out of storage space on her phone!
Solving Two-Step Equations exercise
-
Determine the equation describing the situation.
HintsIf one of your favorite band's album costs $~\$12$ then the total cost of buying four of albums is $4\times \$12=\$48$.
The total battery power she needs to take photos and record the video should be equal to the remaining power.
SolutionHow many photos can Shannon take and still have enough battery power left to record a video?
- First we assign the unknown number of photos to the variable $x$.
- One photo uses $2\%$ of the battery so at most, Shannon can take $x\times 2$ photos.
- Because the video requires $8\%$ of the battery, the total battery life Shannon needs is $x\times 2\%+8\%$ (without the percent signs).
- On the other side of the equation, we write the remaining battery life: $30\%$.
$x\times 2\%+8\%=30\%$.
To solve the equation, we leave out the $\%$ sign:
$x\times 2+8=30$
We can solve the equation using the following steps:
$\begin{array}{rcl} x\times 2+8 & = & ~30\\ \color{#669900}{-8} & &\color{#669900}{-8}\\ x\times 2 & = & ~22 \\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x & = & ~11 \end{array}$
-
Solve the equation.
HintsWe have to do two steps:
- add or subtract and
- multiply or divide.
Use the opposite operator:
- $+~\longleftrightarrow~-$ and
- $\times~\longleftrightarrow~\div$.
Imagine an equation as a scale in balance.
Removing a weight from only one side leads to an imbalance.
SolutionLook at the two steps for solving equations:
- add or subtract and
- multiply or divide.
Next we divide by $2$ on both sides of the equation. This is the opposite of multiplication:
$x=11$.
So, Shannon could take 11 photos and still have enough power left to record a video.
-
Determine how many photos Shannon and her friends can take.
HintsThe equation looks quite similar to $x\times 2+8=30$.
Think about what the numbers mean and what you have to change.
Use opposite operations to solve the equation.
Think about whether the number of photos you can take increases or decreases if you have more battery power.
SolutionThe equations we use for each friend's situation look closely resemble $x\times 2+8=30$.
Anne
$\begin{array}{rcl} x\times 2+8 &=&~20\\ \color{#669900}{-8} & & \color{#669900}{-8}\\ x\times 2 &=& ~12 \\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x &=&~~~6 \end{array}$
Anne can take six photos.
George
$\begin{array}{rcl} x\times 2+8 &=&~24\\ \color{#669900}{-8} & &\color{#669900}{-8}\\ x\times 2 &=&~16 \\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ x &=&~~~8 \end{array}$
George can take eight photos.
Linda
$\begin{array}{rcl} x\times 2+8 &=&~32\\ \color{#669900}{-8} & & \color{#669900}{-8}\\ x\times 2 &=&~24\\ \color{#669900}{\div 2} & &\color{#669900}{\div 2}\\ x &=&~12 \end{array}$
Linda can take twelve photos.
Paul
$\begin{array}{rcl} x\times 2+8 &=&~40\\ \color{#669900}{-8} & & \color{#669900}{-8}\\ x\times 2 &=&~32\\ \color{#669900}{\div 2} & & \color{#669900}{\div 2}\\ x &=&~16 \end{array}$
Paul can take sixteen photos.
-
Solve the following equations.
HintsUse two steps:
- Simplify the equation.
- Isolate the variable by using opposite operations.
Each solution is a natural number.
You can check your solution by substituting your answer for $x$ back into the equation.
SolutionEach of the following equation will be solved in the same manner. We use two steps:
- Simplify the equation.
- Isolate the variable by using opposite operations.
First equation
$\begin{array}{rcl} x\div 4-2&=&~~~1\\ \color{#669900}{+2}&&\color{#669900}{+2}\\ x\div 4&=&~~~3\\ \color{#669900}{\times 4}&& \color{#669900}{\times 4}\\ x&=&~12 \end{array}$
Second equation
$\begin{array}{rcl} x\times 4-2&=&~10\\ \color{#669900}{+2}&&\color{#669900}{+2}\\ x\times 4&=&~12\\ \color{#669900}{\div4}&=&\color{#669900}{\div4}\\ x&=&~~~3 \end{array}$
Third equation
$\begin{array}{rcl} x\times 5+3&=&~~123\\ \color{#669900}{-3}&&\color{#669900}{~-3}\\ x\times 5&=&~~120\\ \color{#669900}{\div5}&&\color{#669900}{~\div5}\\ x&=&~~~~24 \end{array}$
Fourth equation
$\begin{array}{rcl} x\div 5+3&=&~~~4\\ \color{#669900}{-3}&&\color{#669900}{-3}\\ x\div 5&=&~~~1\\ \color{#669900}{\times 5}&&\color{#669900}{\times 5}\\ x&=&~~~5 \end{array}$
-
Describe how to solve two-step equations.
HintsUse Opposite Operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
SolutionTo solve algebraic equations, you must isolate the variable by using Opposite Operations.
For solving two-step equations, you have to use Opposite Operations twice. First use Opposite Operations to remove the constant then again to remove the coefficient to the variable.
Use Opposite Operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
$3\times x-4=8$.
Step 1
- Since we have $-4$ on the left side of the equation, we should add $4$ on both sides of the equation to get $3\times x=12$.
- In order to isolate the variable $x$, we use the Opposite Operation of multiplication, which is division. So we divide by $3$ on both sides of the equation to get $x=4$.
-
Set up an equation to model the situation.
HintsTo write an equation for each store, write the total amount Ben and his siblings can spend, $200$, on the right side of the equal sign. On the left side of the equal sign, write the sum of the cost of the game system, and the unknown number of games times the cost of each game.
Use two steps:
- Simplify the equation.
- Isolate the variable by using opposite operations.
For example if Ben and his siblings went to J&S E-Games, like they always do, they could have bought the game system for $\$112.00$ and each game for $\$16.00$.
If we set up the equation, we get:
$x\times \$16.00+\$112.00=\$200$
- Subtract $\$112.00$: $x\times \$16.00=\$88.00$
- Divide by $\$16.00$: $x=5$
SolutionFirst we need an equation that describes the situation:
$\text{number of games}\times \text{price per game} + \text{game system price} =200$.
Remember, we're calling the number of games Ben and his siblings can buy $x$.
Tami's Toys
- $\$138.00$ for the game system
- $\$15.50$ for each game
So Ben and his siblings could buy $4$ games at Tami's Toys.
The Ice Bear
- $\$126.50$ for the game system
- $\$10.50$ for each game
So Ben and his siblings could buy $7$ games at The Ice Bear.
Punju's Palace
- $\$97.50$ for the game system
- $\$10.25$ for each game
So Ben and his siblings could buy $10$ games at Punju's Palace.
The Gold Pig
- $\$145.00$ for the game system
- $\$5.00$ for each game
So Ben and his siblings could buy $11$ games at The Gold Pig.


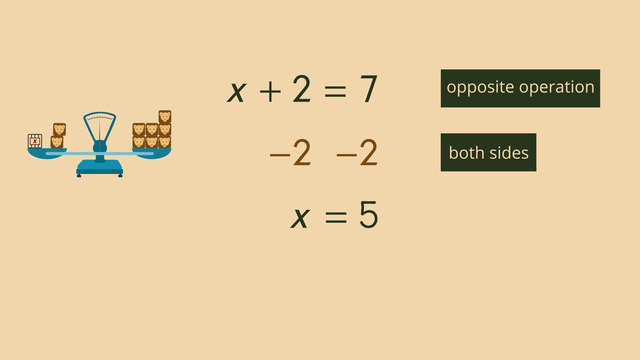













my phone be like: 55%...5 minutes later. 10%
Good video! Also, hi!
:)
that means hi in some langauge wait it means thank you oh well
merci
hola