Solving One-Step Equations
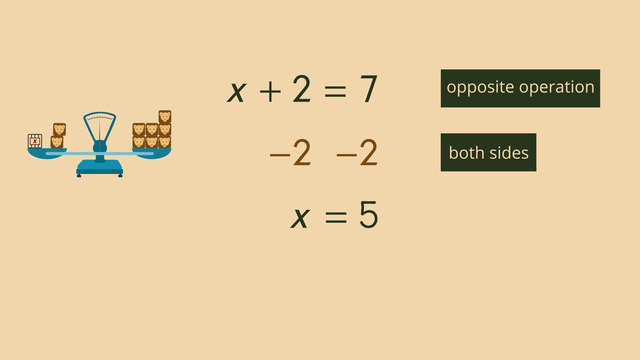

Basics on the topic Solving One-Step Equations
When solving algebraic equations, your goal is to isolate the variable on one side of the equal sign. To do this, think about a balance scale. To keep the scale balanced, whatever amounts you add or subtract to one side of the scale you must do to the other. Likewise for multiplication and division.
For one-step equations, with just one step, you can calculate the value of the variable by doing the opposite operation (inverse operation). If a number is added to the variable on one side of the equal sign, to isolate the variable, leaving it alone on one side of the equal sign, subtract the number from both sides of the equal sign. If a number is subtracted from the variable, to isolate the variable, add the number to both sides of the equal sign, in one step.
For multiplication and division, follow the same strategy, isolate the variable by doing the opposite operation on both sides of the equal sign. If a number is multiplied with the variable, the opposite operation is to divide and vice versa.
Most important is to always keep the equation balanced. Whatever you do to one side of the equation, you must do to the other. Remember the opposite of subtraction is addition, and the opposite of multiplication is division.
Explain steps to solve algebraic equations. CCSS.MATH.CONTENT.HSA.REI.A.1
Transcript Solving One-Step Equations
Today, something happened at the zoo. Some baby lions have run away. There are only 2 out of 7 baby lions left in the cage. How many baby lions do the zookeepers need to catch?
One-step Equations Example 1
To solve this we can use a one-step equation with a variable. Let x represent the number of missing baby lions. To this we can add the 2 that did not escape. This equals 7, which is the total number of baby lions in the zoo.
An equation is like a scale. On the left side of the scale, you have a box for the number of missing baby lions, which are represented by x. In addition, you have 2 baby lions that are remaining. On the right side of the scale, you have the total of 7 baby lions in the zoo.
Now, the scale is in balance. If you take one lion baby away from the left side of the scale, the scale becomes unbalanced. So, you have to take away the same amount, one lion, from the other side. This gets the scale back in balance.
If you take away one more baby lion from the left side, and you take away one more from the right side, you see the box for the missing baby lions is equal to 5. So, there are 5 baby lions missing.
Solving an one-step Equation algebraically
This is basically how equations work. Keep the scale in mind when you solve an equation algebraically.
Our goal here is to isolate x. To get rid of the plus 2 on the left side of the equation, we use the opposite operation. In this case, the opposite of adding 2 is subtracting 2.
Remember our scale. What you do to one side of the equation, you have to do to the other side of the equation. So, we take away 2 from the right side of the equation as well: x + 2 − 2 = x on the left side, 7 − 2 = 5 on the right side. So, our equation now says x = 5.
One-step Equations Example 2
Let's look at another example. The equation is 3 times x = 30. To isolate the x, you use the opposite operation. The opposite operation of multiplying is dividing. So, in this case we divide by 3.
Remember that what you do to one side of the equation, you have to do to the other side of the equation, so we divide this side by 3 as well: 3 · x ÷ 3 = x and 30 ÷ 3 = 10 on the right side. So, our equation now says x = 10.
Rules how to solve one-step Equations
So remember:
- To isolate x, use the opposite operation again.
- The opposite operations of addition is always subtraction and vice versa.
- The opposite operation of multiplication is always division and vice versa.
- What you do to one side, you have to do to the other side.
Let's get back to the baby lions. It is already 5 o’clock and 4 out of the 5 missing baby lions are back, but one is still missing.
Look! what is happening in the snake house? It seems like our baby lion is in trouble – phew, its just the British tea snake.
Solving One-Step Equations exercise
-
Write an equation that best represents the number of missing baby lions.
HintsAn equation is like a scale: both sides of the scale have to have the same value in order to be in balance.
The $x$ in the equation represents the number of missing baby lions.
The total number of baby lions in the zoo is $7$, which represents one side of the equation.
The other side of the equation also represents the total number of baby lions in the zoo, but this time we have the unknown number of missing baby lions, $x$, and the number of baby lions that are still in the cage, $2$.
SolutionTo write this real world problem as a math equation, it helps if we think of the equation as a scale that must be balanced.
We know the total number of baby lions in the zoo: $7$.
What we want to know is the number of missing baby lions, so we assign this unknown quantity to the variable $x$. We know that the total number of baby lions is the number of missing baby lions plus the number of baby lions that are still in the cage. This can be represented by the expression $x + 2$.
This expression must be equal to the total number of baby lions, $7$. Writing out the full equation, we get $x + 2 = 7$, where $x$ represents the number of missing baby lions.
-
Describe how to solve a one-step equation.
HintsLet's take a look at an example:
- $x+2=7$
Let's see:
$\begin{array}{rcr} x+2 &=&7\\ \color{#669900}{~~+2} & ~~ &\color{#669900}{+2}\\ x+4 &=&9\\ \end{array}$
Hmm, as we can see, the equation is more difficult than before and the $x$ is still not isolated. Can you guess what we should have done?
So, if we want to isolate $x$ in the equation $x+2=7$ it doesn't really make sense to add $2$ on both sides of the equation. Instead, subtracting $2$ on both sides should do the trick. Let's see:
$\begin{array}{lcr} x+2 & =& 7\\ \color{#669900}{~~-2} & ~~ & \color{#669900}{-2}\\ x & = & 5 \end{array}$
Great. as you can see, the $x$ is isolated on the left side.
To get rid of a term on one side of an equation, you have to use the opposite operation.
SolutionWhen you solve an equation, you have to isolate the variable on one side of the equation. To do so, you must use the opposite operation of the term you want to get rid of.
Remember, an equation is like a balanced scale, so whatever you do to one side, you have to do the other.
The opposite operation of addition is subtraction, and vice versa. Let's take a look at two examples:
$\begin{array}{lcr} x+2 & = & 7\\ \color{#669900}{~~-2} & ~~ & \color{#669900}{-2}\\ x & = & 5 \end{array}$
Since we have a $-4$, we have to do the opposite operation, $+$, to both sides of the equation:
$\begin{array}{lcr} x-4& = & 8 \\ \color{#669900}{~~+4} & ~~ & \color{#669900}{+4}\\ x & = & 12 \end{array}$
The opposite operation of multiplication is division, and vice versa. Let's take a look at two examples:
$\begin{array}{lcr} x \times 2 & = & 10\\ ~~ \color{#669900}{\div 2} & ~~ & \color{#669900}{\div 2}\\ x & =&5 \end{array}$
Now we perform the opposite operation of $\times$, $\div$:
$\begin{array}{lcr} x\div 2 & = & 3\\ ~~ \color{#669900}{\times 2} & ~~ & \color{#669900}{\times 2}\\ x & = & 6 \end{array}$
-
Find out how many giraffes belong to the giraffe family.
HintsThe number of giraffes is a natural number not a fraction. You can't have 1/2 of a giraffe!
The opposite operation of addition is subtraction, and vice versa.
The opposite operation of multiplication is division, and vice versa.
To isolate the variable, you must carry out the opposite operation of the term you want to move on both sides of the equation.
SolutionWe know the number of missing giraffes, $4$. We also know that the number of missing giraffes is a third of the total number, which is unknown. We represent the unknown number with the variable $x$.
One third of $x$ can be expressed mathematically as $x\div 3$. To find the total number of giraffes, we set $x\div 3$ equal to $4$ and solve for $x$.
$x\div 3=4$.
To do this, we have to do the opposite of $x\div3$ on both sides of the equation. By multiplying by $3$ on both sides of the equation, we get our solution: $x=12$.
There are $12$ giraffes in total.
-
Find the solution for the following equations.
HintsThe opposite operation of addition is subtraction, and vice versa.
The opposite operation of multiplication is division, and vice versa.
To check your work, you can plug the solution for $x$ into the original equation. If your answer checks out, you will have a true math statement.
Remember, to isolate a variable, use the opposite operation on both sides of the equation to remove terms.
SolutionWe can solve equations by isolating the variable $x$. Then we solve for $x$ using opposite operations.
Let's try it with several examples.
The opposite operation of addition is subtraction, and vice versa:
$\begin{array}{lcr} x+3 & = & 12\\ ~~\color{#669900}{-3} & ~~ & \color{#669900}{-3}\\ x & = & 9 \end{array}$
Let's do the same with subtraction:
$\begin{array}{lcr} x-7 & = & 5\\ ~~\color{#669900}{+7} & ~~ & \color{#669900}{+7}\\ x & = & 12 \end{array}$
The opposite operation of division is multiplication, and vice versa:
$\begin{array}{lcr} x \times 2 & =& 16\\ ~~ \color{#669900}{\div 2}& ~~ & \color{#669900}{\div 2}\\ x & = & 8 \end{array}$
Let's do the same with division:
$\begin{array}{lcr} x \div 5 & = & 3\\ ~~\color{#669900}{\times 5} & ~~ & \color{#669900}{\times 5} \\ x & = & 15 \end{array}$
-
Determine the correct steps needed to solve an equation.
HintsHow does a scale work? Both sides of the scale must have equal weights in order to be in balance.
Whatever you do on one side of an equation, think of what you have to do the other side of the equation in order to keep it in balance.
SolutionAn equation is defined by two expressions joined by an equal sign.
The equal sign is like the middle of a scale. The equation corresponds to a balanced scale. If you take away something on one side of the scale, you have to do the same on the other side as well. Otherwise, the scale isn't in balance any longer.
The same concept applies to equations:
$\begin{array}{lcr} x+2 & = & 7\\ ~~\color{#669900}{-2} & ~~ & \color{#669900}{-2}\\ x & = & 5 \end{array}$
The operations we have learned so far are:
- You can add or subtract a term on both sides of an equation.
- You can multiply both sides of an equation by the same, non-zero term.
- You can divide both sides of the equation by the same, non-zero term.
-
Solve the following equations.
HintsEach solution is a multiple of $10$.
Carry out the opposite operation
- $+\longleftrightarrow -$
- $\times \longleftrightarrow \div$
The greatest solution is $x=50$.
SolutionTo solve equations, we have to isolate the variable $x$ using opposite operations.
- The opposite operation of addition is subtraction, and vice versa.
- The opposite operation of multiplication is division, and vice versa.
$\begin{array}{lcr} x \times 3 & = & 60\\ ~~ \color{#669900}{\div 3} & ~~ & \color{#669900}{\div 3}\\ x & = & 20\\ ~&~&~\\ ~&~&~\\ x+15 & = & 45\\ ~~\color{#669900}{-15} & ~~ & \color{#669900}{-15}\\ x & = & 30\\ ~&~&~\\ ~&~&~\\ x \div 5 & = & 8\\ ~~ \color{#669900}{\times 5} & ~~ & \color{#669900}{\times 5}\\ x & = & 40\\ ~&~&~\\ ~&~&~\\ \end{array}$
The greatest $x$ value is:
$\begin{array}{lcr} x-10 & = & 40\\ ~~ \color{#669900}{+10} & ~~ & \color{#669900}{+10}\\ x & = & 50 \end{array}$


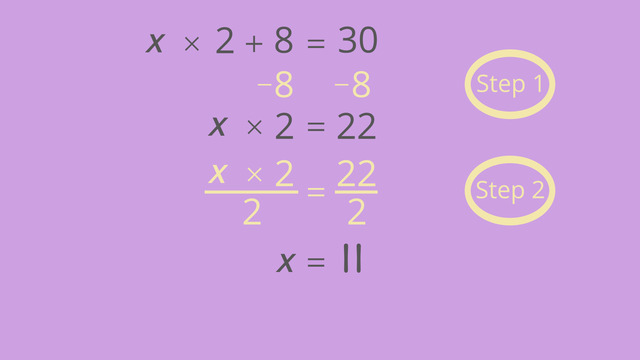













this is so simple
Hi @Mcweinman2134, I guess you write about question number 3 in the interactive practice problems?
This is a drag&drop question type. The words and formulas to fill in the blanks are in a box below. To check your answer please scroll down and press the button "check answer". Then you get a feedback if it's right or wrong. You have 3 tries to answer every question. In the offline version of the worksheets you find all solutions on the last pages of the pdf.
I hope I could help.
Julia
hey there: where/how do I fill in the blanks on the Homework sheets? and how do do I check them? you are not very organized in some lessons do I need a PDF? to work this?