Solving Multi-Step Equations with Variables on Both Sides


Basics on the topic Solving Multi-Step Equations with Variables on Both Sides
To solve complicated variable equations such as those with variables on both sides of the equal sign, remember what you know about the balance scale – you must perform the same operation on both sides of the scale in order to stay balanced.
There are many steps to solve multi-step equations, hence the name. Step 1, if parentheses are shown in the equation, you may need to use the Distributive Property to simplify. Step 2, combine like terms on each side of the equal sign.
Like terms can be constants, variables alone, or variables with coefficients. Constants are numbers alone such as 3 or 1.5. Coefficients are numbers that are attached to a variable as a result of multiplication or division such as 2x or x/4.
Step 3, use the inverse operations (opposite operations) of addition or subtraction to move constants to one side of the equal sign and variables to the other. Use common sense, and do this in the most efficient manner. Next is Step 4, use inverse operations of multiplication or division to isolate the variable and calculate the answer. It’s always a good idea to check your work by substituting the solution for the variable back into the original equation and use PEMDAS to simplify.
Explain steps to solve algebraic equations. CCSS.MATH.CONTENT.HSA.REI.A.1
Transcript Solving Multi-Step Equations with Variables on Both Sides
Meet Emilio and Joanna. They're at a fish store. They've come to buy some scaly friends, and they each have the same amount of money.
Emilio makes his selection quickly. He buys two Rainbow Blinkeys and ten Grey Borings. Joanna loves Rainbow Blinkeys, so she buys five of them and just one Grey Boring. They both spend all of their money.
When Emilio sees Joanna’s purchase, he feels sad because he realizes he could have bought another Rainbow Blinkey. He wonders, to get one more Rainbow Blinkey, how many Grey Borings would he need to exchange? To find out how many, Emilio can use a multi-step equation with variables on both sides of the equal sign.
Multi-step Equation Example 1
Just to refresh your memory, an equation works like a scale. And to keep the scale balanced, when you add or subtract one side of the scale, you must perform the same operation to the other side.
Joanna bought five Rainbow Blinkeys and one Grey Boring. For the same amount of money, Emilio bought two Rainbow Blinkeys and ten Grey Borings so the scale is balanced.
Grey Borings cost $1 each. We can write the expression 5x + 1 = 2x + 10 to represent this situation, where the variable x represents the cost of a Rainbow Blinkey.
To find out how many Grey Borings are equal to the cost of one Rainbow Blinkey, you need to isolate the Xs. Using inverse operations, we can modify the equation so we will have all the Xs on one side of the equal sign and all the constants on the other side: 5x + 1 = 2x + 10.
- First, let’s subtract one from both sides of the equation: 5x = 2x + 9.
- Next, subtract 2x from both sides of the equation. The scale is still balanced: 3x = 9.
- To isolate the x, use the opposite of multiplication. Divide by 3 on both sides of the equation.
What is the result? 3x ÷ 3 = 9 ÷ 3x = 3, which means the cost of one Rainbow Blinkey is equal to the cost of three Grey Borings. Emilio can exchange three Grey Borings and get one more Rainbow Blinkey. Emilio is happy!
Multi-step Equation Example 2
Now that we have reviewed the basics, let's take a look at a more complicated problem: 3 · (2x − 5) + 10 = 4x + 9.
- See the parentheses? Use the Distributive Property and multiply each of the terms inside the parentheses by three: 2x · 3 = 6x and −5 · 3 = −15. So we get 6x − 15 + 10 = 4x + 9.
- To stay organized, on each side of the equal sign, combine any like terms as you go through the problem. So we get: 6x minus 5 = 4x + 9.
- Next, use inverse operations to move the variables with coefficients to one side of the equation and the constants to the other. Remember to be strategic when you choose which side to move the terms.
- Alright, Let’s move! First we deal with the constant and add 5 to each side of the equal sign. So we get: 6x = 4x + 14. Now, subtract 4x from each side of the equal sign. 2x = 14.
- Next, use the inverse operation to solve for x. Divide both sides of the equation by 2, x = 7!
As you can see, it's important to go step-by-step when solving equations such as this. I wonder how the fish are doing. Let’s take a look.
So peaceful… Hold the fish food! What's going on? Wow, talk about fight or flight! Look at those fish move!
Solving Multi-Step Equations with Variables on Both Sides exercise
-
Determine how many Grey Borings Emilio needs to exchange to buy one more Rainbow Blinkey.
HintsImagine an equation as a scale in balance.
Whenever you add or subtract a value or term from one side of an equation, you have to do it on the other side of the equation as well. Otherwise, it doesn't stay in balance.
If one Rainbow Blinkey costs $x$, for example, three Rainbow Blinkeys cost $3x$.
SolutionEmilio would like to know how many Grey Borings he needs to exchange so he can buy one more Rainbow Blinkey. First, we assign the cost of one Rainbow Blinkey to the variable $x$.
Joanna buys $5$ Rainbow Blinkeys and only one Grey Boring. So Joanna spends $5x+1$. Emilio buys $10$ Grey Borings and $2$ Rainbow Blinkeys that cost $2x+10$. Since they spend the same amount of money, we set our two expressions equal to each other.
$5x+1=2x+10$
Imagine a scale in balance. Each operation has to be performed on both sides of the scale:
- subtract $1$: $5x=2x+9$
- subtract $2x$: $3x=9$
- divide by $3$: $x=3$
-
Decide which steps are needed to solve the equation $3\times (2x-5)+10=4x+9$.
HintsImagine an equation as a scale in balance. After we combine like terms, we have to Isolate the Variable. Each operation we perform, we have to perform on both sides of the equation.
Use Opposite Operations:
- Addition $\longleftrightarrow$ Subtraction, and vice versa
- Multiplication $\longleftrightarrow$ Division, and vice versa
Remember to always solve equations step-by-step.
SolutionHere, we'll see how we can solve a more complicated equation using different mathematical rules by going step-by-step. The equation we want to solve is $3\times(2x-5)+10=4x+9$.
- First, we use the Distributive Property to get rid of the parentheses.
- That leaves us with $6x-15+10=4x+9$.
- Then, we combine like terms.
- Doing this gives us $6x-5=4x+9$.
- Next, we add $5$ on both sides, which gives us $6x=4x+14$.
- Subtracting $4x$ from both sides will leave us with $2x=14$.
- Finally, dividing by $2$ gives us the solution $x=7$.
-
Find the right equations for the fish on the scale.
HintsIf you buy one goldfish for the price of $x$, $4$ goldfish will cost $4x$.
You have to add the costs of the different types of fish.
SolutionLet's start with the scale on the left:
- We see $2$ goldfish and $6$ Rainbow Blinkeys on the left side of the scale. This gives us the expression $2x+6$.
- On the right side of the scale are $4$ goldfish and $2$ Rainbow Blinkeys, leading to the expression $4x+2$.
- Because Joanna and Emilio spend the same amount of money, we set our two expressions equal to each other, giving us $2x+6=4x+2$.
- We see $3$ goldfish and $2$ Grey Borings on the left side of the scale. This gives us the term $3x+2$.
- On the right side of the scale are $2$ goldfish and $5$ Grey Borings. So we get $2x+5$.
- Because Joanna and Emilio spend the same amount of money, our final equation is $3x+2=2x+5$.
- We see $4$ goldfish on the left side of the scale, $4x$.
- On the right side of the scale are $1$ goldfish and $9$ Grey Borings. This gives us the term $x+9$.
- Because Joanna and Emilio spend the same amount of money, our final equation is $4x=x+9$.
-
Decide when the numbers of inhabitants match.
HintsIf $50$ people move away after one year, then $100$ people move away after two years.
You can solve an equation by using opposite operations:
- The opposite operation for addition is subtraction, and vice versa.
- The opposite operation for multiplication is division, and vice versa.
When the number of inhabitants in both villages match, there will be $2,600$ people in each village.
SolutionIn general, we solve algebraic problems with variables on both sides by following these steps:
- We assign the variable $x$ to the unknown number. In this problem, it's the number of years.
- Next, we define expressions according to the story:
- village Addition $2000+150x$
- village Subtraction $3000-100x$
How do we solve the equation? To solve, isolate the variable $x$.
- First, we arrange the equation so that all constants are on one side of the equal sign and the variables on the other. In order to do this, we use opposite operations to move the terms.
- Subtracting $2000$ on both sides gives us $150x=1000-100x$.
- Now we add $100x$ on both sides to get $250x=1000$.
- Finally, we divide by $250$, which gives us $x=4$.
-
Evaluate how we can solve an equation.
HintsLook at the scale above. What do you see?
In the middle of the scale you can imagine an equal sign.
Both sides of an equal sign represent the same value.
If you only put a weight on the left side of a scale, the scale will be imbalanced. Since you want the scale to be balanced, you have to put the same weight on the right side as well.
SolutionSolving an equation can be thought of as a scale in balance.
In the middle of an equation there is an equal sign. On both sides we find equal terms.
Back to the scale: each operation has to be performed on both sides. Otherwise the scale will not be in balance. For example, in order to solve the equation $3x=9$, we have to divide both sides by $3$. That will leave us with $x=3$.
Remember the rules concerning opposite operations:
- the opposite operation of addition is subtraction, and vice versa
- the opposite operation of multiplication is division, and vice versa
-
Solve the following equations.
HintsUse the Distributive Property to simplify, if necessary. For example: $3\times(x+2)=3x+6$.
Combine like terms on one or both sides of the equation.
Isolate the variable $x$ by using Opposite Operations.
SolutionBecause you've learned already a lot, we should practice, but this time let's evaluate equations that are more complicated. The concept always stays the same. Step by step, if it's necessary:
- First we use the Distributive Property.
- Next, we Combine Like Terms.
- Then, we move the constants to the right side and the variables to the left, or vice versa.
- Finally, we divide on both sides to get the solution.
Using the same steps, we solve two more equations:
$\begin{array}{rcrcl} 5\times(x+2)-20&=&3\times(x+1)-5\\ 5\times x+10-20&=&3\times x+3-5&&|\text{ Distributive Property}\\ 5x-10&=&3x-2&&|\text{ Combine Like Terms}\\ \color{#669900}{+10}&&\color{#669900}{+10}&&| (-~\leftrightarrow~+) \text{ Opposite Operations}\\ 5x&=&3x+8\\ \color{#669900}{-3x}&&\color{#669900}{-3x}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 2x&=&8\\ \color{#669900}{\div2}&&\color{#669900}{\div2}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&4 \end{array}$
... and ...
$\begin{array}{rcrcl} 12\times(x-1)&=&5x+23\\ 12x-12&=&5x+23&&|\text{ Distributive Property}\\ \color{#669900}{+12}&&\color{#669900}{+12}&&| (-~\leftrightarrow~+) \text{ Opposite Operations}\\ 12x&=&5x+35\\ \color{#669900}{-5x}&&\color{#669900}{-5x}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 7x&=&35\\ \color{#669900}{\div7}&&\color{#669900}{\div7}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&5 \end{array}$


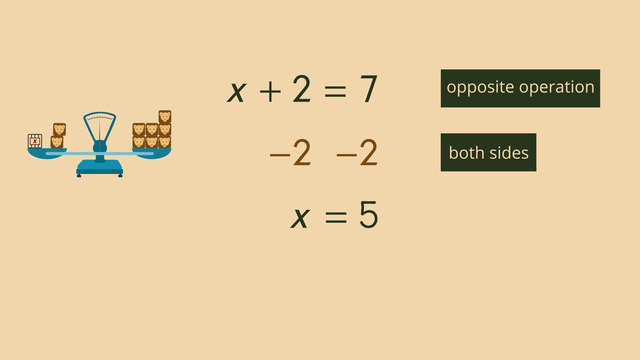
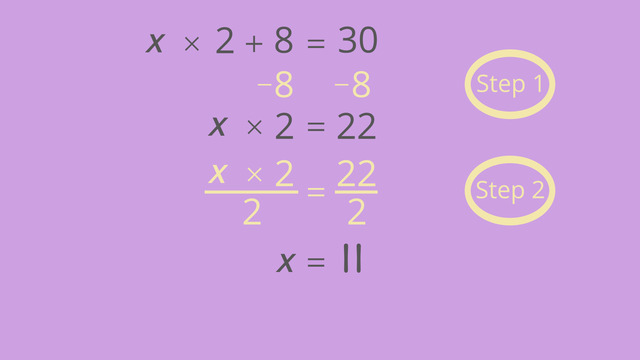












-4y+2(y+5)=18