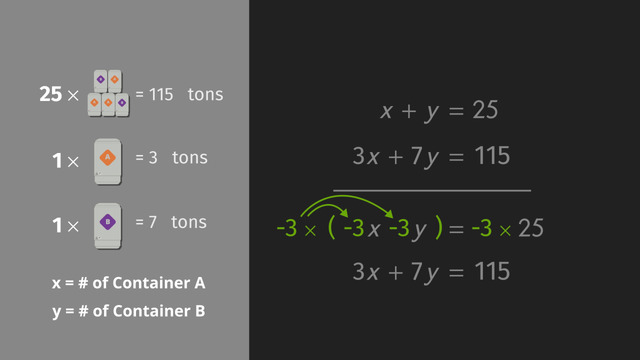Solving Systems of Inequalities


Basics on the topic Solving Systems of Inequalities
One way of finding the solution set of a system of linear inequalities in two variables is by graphing.
To graph a system of linear inequalities and see its solution set, first graph the corresponding system of linear equations. While graphing these equations, use either solid or dashed lines: use solid lines for “is greater than or equal to” (≥) or “is less than or equal to” (≤) inequalities, and dashed lines for “is greater than” (>) or “is less than” (<) inequalities.
Use the point of origin (0,0), or another point of your choice if the origin does not work, as a test point to determine the correct half-plane that corresponds to the graph of each inequality and lightly shade in that half-plane. Finally, the solution to the system of linear inequalities is the region where all the shaded half-planes overlap.
Graphing systems of linear inequalities has valuable applications in business, especially in making important decisions to maximize profit and minimize cost.
Represent and solve equations and inequalities graphically.
CCSS.MATH.CONTENT.HSA.REI.D.12
Transcript Solving Systems of Inequalities
Caleb is very proud of his collection of sneakers and baseball caps. He wants to build a shelving unit to display his treasures. In his garage, he finds 150 nails and 66 wooden planks. Can we help Caleb figure out if there will be enough materials to build the shelving unit?
Solving a system of inequalities
It's no problem at all! To calculate the solution, you can solve a system of inequalities. Caleb knows that, to build a cubby for each baseball cap, he needs 5 nails and 2 wooden planks. Let 'b' equal the number of baseball caps. To build a cubby for each pair of sneakers, he needs 5 nails and 3 wood planks. Let 's' equal the number of pairs of sneakers. Although he has 150 nails and 66 planks to build the shelf, he doesn't have to use them all. Let’s write the two inequalities.
Caleb uses 5 nails for each baseball cap cubby and 5 nails for each sneaker cubby, and the total is less than or equal to 150 nails. He also uses 2 wooden planks for each baseball cap and 3 planks for each pair of sneakers. Caleb can use 66 wooden planks or fewer to construct his cubbies.
Does Caleb have enough materials to build a shelf to display 10 baseball caps and 15 pairs of sneakers? To figure this problem out, let’s substitute 'b' with the number 10 and 's' with the number 15. Simplify by multiplying, and then add. Since both inequalities are true, we know Caleb has enough materials to build the shelving unit. If only one of the inequalities were true, then he would only have enough of one of the materials he needs to build the shelf.
Caleb wants to know if he has enough materials to build cubbies for 5 new pairs of shoes. Instead of 15, we'll substitute the number 20 in our system of equations. He'll have enough nails to complete this project, but he won't have enough wooden planks to finish building the extra cubbies.
Graphing a system of inequalities
We can also figure out the answer to this system of inequalities problem by graphing. To make it easier to graph, let's modify the original equation to let 'x' represent the number of baseball caps and 'y' to represent the number of pairs of sneakers. Next, we need to rewrite the two inequalities in slope-intercept form. To do this, you must isolate the 'y' on the left side of the inequality sign, so subtract the x-term from both sides, and then divide both sides by the coefficient 5 to isolate 'y'. Y' is alone on the left side. Let's do the same to the other equation and the two inequalities are now written in slope-intercept form.
Solving the problem graphically
Now it's much easier to graph each inequality. For the first inequality with a y-intercept equal to 30 and a slope equal to -1, the line and the yellow shaded area of the graph are included in the solution set of the inequality; and for the second inequality with a y-intercept of 22 and a slope equal to -2/3, the line and the red shaded area of the graph are included in the solution set. The orange shaded area of the graph is the overlap of the yellow and red shaded areas, and it’s the solution to this system of inequalities.
Take a look at point 'p', the ordered pair (10, 15), since it’s in the area shaded orange, it’s a possible solution to the system, so we know Caleb has enough nails and planks to build cubbies for 10 baseball caps and 15 pairs of sneakers. On the other hand, point 's', the ordered pair (10, 20), is not in the area shaded orange. From the graph, we can see that Caleb has enough nails, shown by the area shaded yellow, but he does not have enough planks, shown by the area shaded red, to build 10 cubbies for caps and 20 cubbies for sneakers, so point 's' is not a solution.
Although Caleb has enough supplies, he’s not a master with a hammer and, as you can see, the shelving unit looks a little bit unstable he puts the last baseball cap in the cubby, and ...oh no…
Solving Systems of Inequalities exercise
-
Establish the corresponding system of inequalities.
HintsMake sure Caleb can make use of as many nails and wooden boards as possible,
but not more.
To check if Caleb could build enough shelves for 5 baseball caps and 19 pairs of sneakers, plug those values into both of the inequalities.
SolutionCaleb is very proud of his collection of sneakers and baseball caps. To show off his collection, he would like to build a shelving unit for them.
First let's assign variables to the unknown number of baseball caps and sneakers Caleb will be able to store: Let $b$ represent the number of baseball caps and $s$ the number of pairs of sneakers.
Caleb has $150$ nails. He needs $5$ nails per baseball cap and $5$ nails per pair of sneakers. Thus we get $5b+5s\le150$.
The number of wooden boards Caleb has is $66$. He needs $2$ boards per baseball cap and $3$ per pair of sneakers. So we get $2b+3s\le66$.
-
Identify the area containing all solutions to the system of inequalities.
HintsFirst we replace $b$ by $x$ and $s$ by $y$ to get the following system of inequalities:
$\begin{array}{rcl} 5x+5y&\le&150\\ 2x+3y&\le&66 \end{array}$
Next we write each inequality in slope intercept form:
Draw the boundary line of each inequality and check which combinations of $x$ and $y$ satisfy it.
The intersection of both solution sets, including the boundary lines, is the solution set to the system of inequalities.
SolutionWe can solve the system of inequalities by graphing in the following manner:
- First we replace the variables $b$ and $s$ with $x$ and $y$.
$~$
- Next we write each inequality in a slope intercept form.
and
$\begin{array}{rclll} 2x+3y&\le&66\\ \color{#669900}{-2x}&&\color{#669900}{-2x}\\ 3y&\le&-2x+66\\ \color{#669900}{\div 3}&&\color{#669900}{\div 3}\\ y&\le&-\frac23x+32 \end{array}$
$~$
- Finally, draw the boundary lines $y=-x+30$ (in red) and $y=-\frac23x+32$ (in blue). Because we have a $\le$ relation for each equation, the area of the solution set for each inequality lies under each line. The solution set of the system of inequalities is the intersection of both solution sets, including the boundary lines.
-
Determine if the the number of shelves needed could be constructed.
HintsFirst establish the inequality for the number of nails as well as the inequality for the number of wooden boards.
If the resulting number of nails for the given amount of baseball caps and pairs of sneakers is less than or equal to $400$, then the inequality for nails is fulfilled.
SolutionFor Caleb's new shelves, he needs $10$ nails and $4$ wooden boards per baseball cap and $12$ nails and $5$ boards per pair of sneakers. He has $400$ nails and $160$ wooden boards at disposal.
Let $x$ represent the number of baseball caps and $y$ represent the number of pairs of sneakers. We get the following system of inequalities:
$(1)~~10x+12y\le 400$ for the nails,
and
$(2)~~4x+5y\le 160$ for the wooden boards.
$~$
To check if Caleb could construct shelves for $10$ baseball caps and $20$ pairs of sneakers, we put these values into our system of inequalities:
$(1)~~10(10)+12(20)=340\le400$,
and
$(2)~~4(10)+5(20)=140\le160$.
We can now see that Caleb can construct enough shelves for $10$ baseball caps and $20$ pairs of sneakers.
-
Identify which graph belongs to which system of inequalities.
HintsThe blue and red line are the boundary lines: if we have a $\le$ relation, then all solutions lie under the boundary line.
If you have two inequalities, then both must be satisfied.
The solution set of two inequalities is the intersection of both solution sets.
SolutionHow can we graph the solution set of a system of inequalities?
- First we draw the boundary lines of the solutions sets.
- For a $\le$ relation, all solutions lie under the boundary line. For a $\ge$ relation, all solutions lie over the boundary line.
- Draw lines for $\le$ or $\ge$ relations and dashed lines stand for $<$ or $>$ relations.
- The intersection of the solution sets of two inequalities is the solution set of the system of inequalities.
Now let's have a look at the graphs from the left to the right:
The first graph is given by
$\begin{array}{rcl} 5x+3y&\ge&15\\ x+3y&\le&6 \end{array}$
The second graphing is given by
$\begin{array}{rcl} 5x+3y&\le&15\\ x+3y&\le&6 \end{array}$
The third graph is given by
$\begin{array}{rcl} 5x+3y&\le&15\\ x+3y&\ge&6 \end{array}$
And the last, but not least, graph is given by
$\begin{array}{rcl} 5x+3y&\ge&15\\ x+3y&\ge&6 \end{array}$
-
Write each inequality in slope intercept form.
HintsSlope intercept form is given by $y\le mx+b$, where $m$ is the slope and $b$ the $y$-intercept.
You can subtract from both sides:
Keep in mind: You have to change the relation sign if you multiply or divide by a negative number.
SolutionTo get write inequality in slope intercept form, $y\le mx+b$, we perform the following operations:
$\begin{array}{rclll} 5x+5y&\le&150\\ \color{#669900}{-5x}&&\color{#669900}{-5x}\\ 5y&\le&-5x+150\\ \color{#669900}{\div 5}&&\color{#669900}{\div 5}\\ y&\le&-x+30 \end{array}$
and
$\begin{array}{rclll} 2x+3y&\le&66\\ \color{#669900}{-2x}&&\color{#669900}{-2x}\\ 3y&\le&-2x+66\\ \color{#669900}{\div 3}&&\color{#669900}{\div 3}\\ y&\le&-\frac23x+22 \end{array}$
-
Decide what combinations of comic and fantasy books Caleb could buy.
HintsFirst establish the system of inequalities.
Pay attention to signs.
You can graph the solution set.
SolutionFirst we assign $x$ to the number of comics and $y$ to the number of fantasy books.
The total number of books is the sum of each number. So we get
$x+y\ge 5$.
Because Caleb has $24$ dollars, we get the second inequality,
$3x+5y\le 24$.
For getting the solution set we can draw the boundary lines. The intersection of the solution sets is the solution set of the system of inequalities. Last we can check each point in the coordinate system.
The only combinations which don't lie in the solution set are
- 2 comics and 4 fantasy books,
- 5 comics and 2 fantasy books, and
- 3 comics and 1 fantasy book.