Systems of Equations and Inequalities

Content

• Introduction
• Solving Systems of Equations
• Solving Systems of Equations by Graphing
• Solving Systems of Equations by Substitution
• Solving Systems of Equations by Elimination
• Word Problems
• Solving Systems of Inequalties by Graphing

Introduction

A system of equations or inequalties is several equations or inequalities that are solved simultaneously.

Solving Systems of Equations

There are several methods you can use to solve systems of equations problems. To solve these problems, you can graph, or use the substitution or elimination method.

Solving Systems of Equations by Graphing

The solution to this system of equations is where the two lines intersect. Graph each equation then look for the point of intersection on the graph. The point of intersection is where the two equations are equal.

$\begin{align} y_{1}&=3x +4\\ y_{2}&=\frac{1}{3}x + 2\\ \end{align}$

The solution for this system is point $(-0.75, 1.75)$.

Solving Systems of Equations by Substitution

To solve by substitution, manipulate the problem to have just one of the variables then follow steps to solve.

$\begin{align} 3y &=6x + 3\\ 2y &=8x + 4 \end{align}$

To solve this system by substitution, follow these steps. Solve one equation for x or y-value. For this problem, use the first equation and solve for the y-value.

$\begin{align} 3y &=6x + 3\\ \frac{3}{3}y&=\frac{6x+3}{3}\\ y&=2x+1 \end{align}$

Substitute the new value into the other equation – for this problem, the second equation.

$\begin{align} 2y &=8x + 4\\ 2(2x+1)&=8x+4\\ 4x+2&=8x+4\\ 4x+2 -2&=8x+4 -2\\ 4x &=8x+2\\ 4x -8x &=8x -8x +2\\ -4x &= 2\\ \frac{-4}{-4}x&=\frac{2}{-4}\\ x&=\frac{-1}{2} \end{align}$

Next, to solve for y-value, substitute the value for x into one of the equations.

$\begin{align} 3y&=6x + 3\\ 3y&=(6\times\frac{-1}{2}) + 3\\ 3y&=-3 +3\\ 3y&=0\\ y&=0 \end{align}$

The solution to this system is $(\frac{-1}{2}, 0)$

Solving Systems of Equations by Elimination

To solve by elimination, add or subtract to eliminate one variable then solve.

$\begin{align} 2y &= 3x + 2\\ y&=x+4 \end{align}$

Manipulate one equation so you can eliminate one of the variables by adding or subtracting. For this problem, we can multiply the second equation by 2 then subtract it from the first equation.

$\begin{align} 2y &= 3x + 2\\ -2(y&=x+4) \end{align}$

$\begin{align} 2y= 3x + 2\\ \underline{-2y=-2x+ -8}\\ 0=x + - 6\\ x=6 \end{align}$

Next, substitute the x-value into one of the equations to calculate the y-value.

$\begin{align} 2y &= 3(6) + 2\\ 2y&=18 +2\\ 2y&=20\\ y&= 10 \end{align}$

The solution to this system is $(6, 10)$

Although all systems of equations problems can be solved by graphing, substitution, or elimination, select the method that is easiest to use.

Word Problems

Word problems often model real word situations. Set up a system of equations to solve this problem.

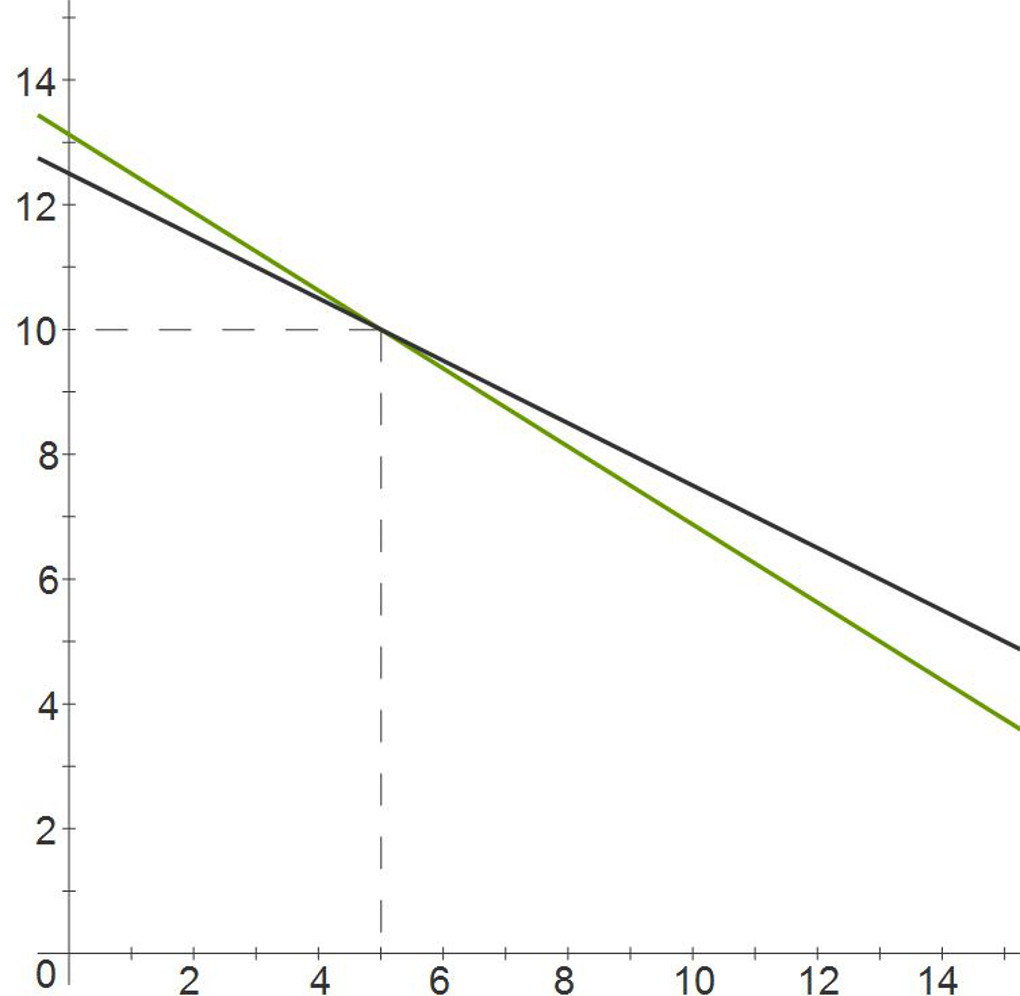
The school ensemble sold tickets for two performances. The equations 25x + 50y = 625 and 40x + 65y = 850 represent the value of the tickets sold for each of the two performances. If x represents the cost of a student ticket and y is the cost of an adult ticket, what is the cost of each ticket?

First set up each equation in the slope-intercept form then graph. The intersection of the two line is the solution for the system.

$\begin{align} 25x + 50y &= 625 \\ 50y &= -25x + 625\\ y &= -0.50x + 12.5 \end{align}$

$\begin{align} 40x + 64y &= 840 \\ 64y &= -40x + 840\\ y &= -0.625x + 13.125 \end{align}$

The solution is point (5, 10).

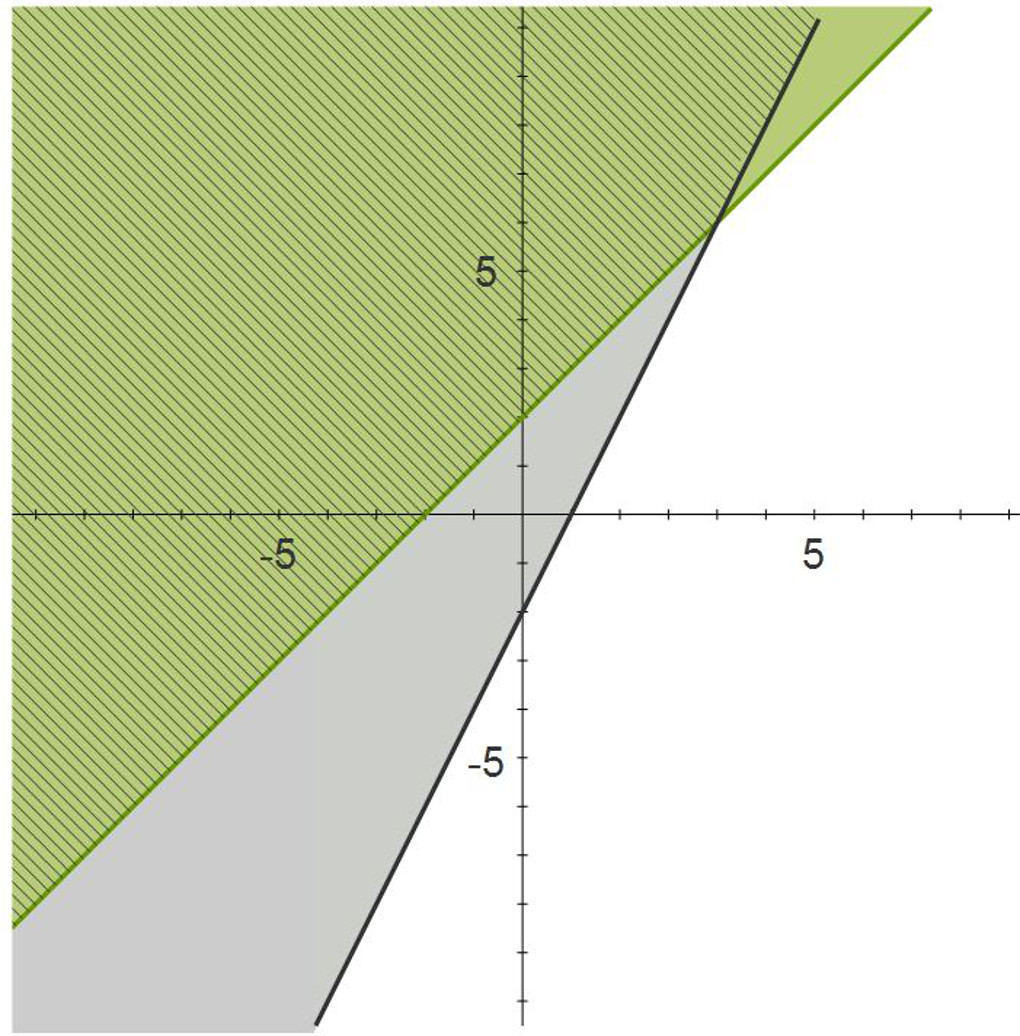
Solving Systems of Inequalties by Graphing

The only way to solve a systems of inequalities is by graphing. Graph each inequality, then determine the area that satisfies all of the inequalities in the system. To check, pick a point in the solution area and verify that it works for all the inequalities in the system.

$\begin{align} y&\geq2x +2\\ y&\geq2x -2 \end{align}$

Verify the solution for both inequalities using the point (0, 5).

$\begin{align} 5&\geq2\times 0 +2\\ 5&\geq 2 \end{align}$

$\begin{align} 5&\geq2\times 0 -2\\ 5&\geq -2 \end{align}$

The solution works for both inequalities.