Solving Systems of Equations by Elimination
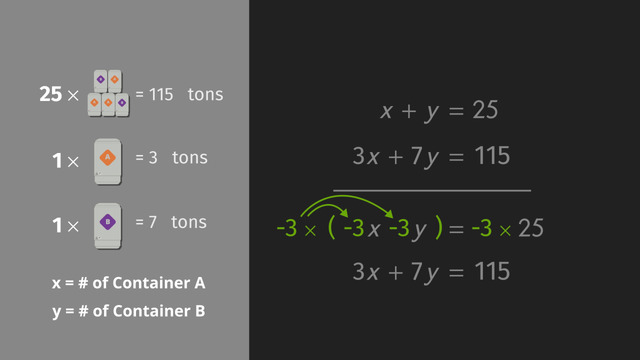

Basics on the topic Solving Systems of Equations by Elimination
A system of equations, also called simultaneous equations, is two or more equations with the same variables. To determine the solution to the system, or the point where the equations intersect, there are several methods: graphing, substitution, and elimination.
This video investigates how to use elimination by addition or subtraction to solve systems of linear equations. To solve by elimination, you must manipulate the system so when adding or subtracting the equations, one of the variables will cancel out, and then you can solve for the remaining variable. After the solution for one variable is calculated, just plug the known value into one of the equations to solve for the second variable. Follow the steps you have learned to isolate the second variable by using inverse operations. Don’t forget, whatever you do to one side of the equal sign you must do to the other.
Also, remember to always check your work by plugging in the values for the variables and making sure the solutions are valid. You would hate to miss the problem because you made a careless error and complicated problems such as these have lots of room for error. There are many real world uses for solving systems of equations such as figuring out how many cupcakes and how many cookies were sold at a soccer team’s bake sale - if a certain amount of money was collected. Anytime you have a problem with the same unknowns, setting up a system of equations may be the best way to solve your problem. To learn more, watch this video.
Solve systems of equations to find solutions to problems.
CCSS.MATH.CONTENT.HSA.REI.C.5
CCSS.MATH.CONTENT.HSA.CED.A.3
Transcript Solving Systems of Equations by Elimination
Far, far away, in a distant universe, in the System of Equations, on a previously unexplored planet called Elimination, a brave, but mathematically-challenged shuttle crew has been tasked with bringing home samples from the planet.
The crew has twenty-five containers to collect samples of material A and material B. They have determined that a container filled with sample A has a mass of three tons, and a container filled with sample B has a mass of seven tons.
In order to return to Earth safely, the filled containers must not have a total mass of more than one hundred fifteen tons. How many containers of each sample can be transported on the space shuttle? Let's help the crew figure out this problem!
Translating a Word Problem into a System of Equations
Since an error in the calculation could mean a major disaster for the space travelers, let’s go over the information one more time.
- There are 25 containers.
- Each container of sample A weighs 3 tons.
- And each container of sample B weighs 7 tons.
- The total allowed is 115 tons.
To describe this situation, we can write two equations then use a system of equations to solve for the two unknowns: x, the number of containers of sample A, and y, the number of containers of sample B.
Let's write it on the board, x + y = 25, and 3x + 7y = 115. Notice how we've line up the variables.
Eliminating Variables
Now let’s manipulate one or both of the equations as needed. We can use addition or subtraction to eliminate one of the variables.
Hmm, how can we eliminate one of the variables? How about we multiply the first equation, x + y = 25, by negative three? We distribute −3 to each term.
Now we can add our two equations. We see that −3x + 3x cancels out to 0x, which is 0, −3y + 7y = 4y, and −75 + 115 = 40… See how the variable x is eliminated?
Solving a System of Equations for the Unknowns
Now, solve for y. We can divide both sides by 4 and see that y is equal to 10. Next, substitute 'y = 10' into one of the original equations, so you can solve for x.
We can use either of the original equations and our answer will be the same; let's save time and pick the least complicated equation.
- When we plug in 10 for y, we have x + 10 = 25.
- Subtract 10 from both sides: x = 15.
The crew learns they can take 15 containers of sample A and 10 containers of sample B. Whew-hoo! Crisis averted!
Hold on! What’s happening? They can’t start ! There's a stowaway! (No problem, they can activate a specially designed wiper, designed especially for an emergency such as this. Watch how that stowaway will be wiped away!)
Solving Systems of Equations by Elimination exercise
-
Examine the following statements.
HintsLet's have a look at the following example:
$\begin{align*} x+y&=4\\ x-y&=2 \end{align*}$
If we add these equations, we can eliminate the variable y. So we get:
$2x=6$
Remember: Usually you need as many equations as you have variables.
You can multiply any equation with any number (exept for zero).
SolutionBecause we have the unknown number of containers of sample A as well as the unknown number of containers of sample B, we write equations with two variables.
Because we have two equations with the same two variables, we have a system of equations:
$x+y=25$ (this equation represents the total number of containers)
$3x+7y=115$ (this equation represents the maximum weight)
For example:
$\begin{align*} x+y&=4\\ x-y&=2 \end{align*}$
If we add the equations we get $2x=6$. This gives us one equation and one variable. We can solve for x by using opposite operations. Dividing by $2$ leads to $x=3$. This value can be plugged into $x+y=4$ to solve for y:
$\begin{array}{rcr} 3+y&=&4\\ -3&=&-3\\ y&=&1 \end{array}$
-
Describe how to solve systems of equations by elimination.
HintsMultiply one or both equations so that the coefficients of either $x$ or $y$ are the same except for their signs.
Use the Distributive Property
$a\times(b+c)=a\times b+a\times c$.
After multiplying, if you add one equation to the other, you can eliminate one equation as well as one variable.
Solve this equation with one variable using opposite operations.
Then plug the value of the known variable into one of the original equations and solve for the second variable.
SolutionConsider the coefficients of $x$ and $y$ in each equation.
Be strategic when determining how to multiply the equation in order to get common coefficients, for example for $x$, but with different signs. So we multiply the first equation by $-3$:
$\begin{align*} -3\times(x+y)&=-3\times 25\\ 3x+7y&=115 .\end{align*}$
Using the Distributive Property this gives us:
$\begin{align*} -3x-3y&=-75\\ 3x+7y&=115. \end{align*}$
Well done, the coefficient of $x$ in the first equation is $-3$ and the coefficients of x in the second equation is $3$.
We add the equations and get:
$4y=40$
Next we divide by $4$ to solve for $y$:
$y=10$
Plug $y=10$ into the first equation:
$x+10=25$
Now, we subtract $10$ on both sides of the equation to get $x=15$.
-
Solve the given systems of equations by elimination.
HintsIn each of the given systems of equations you can add the equations without having to multiply first.
After adding the equations, you still have one equation and one variable. You can solve this equation using opposite operations.
The opposite operation of multiplication is division, and vice versa.
Don't forget the second variable.
It doesn't matter into which of the original equations you plug in the solution of the first variable.
SolutionSo, let's practice elimination:
- Add the equations to eliminate one variable.
- Solve this equation using opposite operations.
- Plug in the solution into any of the original equations to get the solution of the second variable.
$\begin{array}{rcr} 3x-2y&=&7\\ 4x+2y&=&14 \end{array}$
- Add the equations $\rightarrow$ $7x=21$.
- Divide by $7$ $\rightarrow$ $x=3$.
- Substitute $x=3$ into $3x-2y=7$:
Dividing by $-2$ gives us $y=1$.
$~$
(B)
$\begin{array}{rcr} -4x+7y&=&3\\ 4x+2y&=&6 \end{array}$
- Add the equations $\rightarrow$ $9y=9$.
- Divide by $9$ $\rightarrow$ $y=1$.
- Substitute $y=1$ into $4x+2y=6$:
Dividing by $4$ gives us $y=1$.
$~$
(C)
$\begin{array}{rcl} 12x+4y&=32\\ 3x-4y&=13 \end{array}$
- Add the equations $\rightarrow$ $15x=45$.
- Divide by $15$ $\rightarrow$ $x=3$.
- Substitute $x=3$ into $12x+4y=32$:
Dividing by $4$ gives us $y=-1$.
$~$
(D)
$\begin{array}{rcl} 3x+11y&=&22\\ -3x-4y&=&13 \end{array}$
- Add the equations $\rightarrow$ $7y=35$.
- Divide by $7$ $\rightarrow$ $y=5$.
- Substitute $y=5$ into $3x+11y=22$:
Dividing by $3$ gives us $x=-11$.
-
Determine how much pocket money Ben and Sam get each day.
HintsFirst you need to have a system of equations: two equations and two variables.
- We add the equations or subtract one equation from the other to eliminate one variable.
- We solve this equation using opposite operations.
- We plug this solution into any of the original equations to get the solution of the other variable.
SolutionFirst we have to set up a system of equations according to the described situation.
We know that together each week, Sam and Ben get daily pocket money equal to 56 dollars a week. $x$ represents Sam's daily pocket money, and $y$ represents Ben's daily pocket money for a normal week. This gives us the first equation:
$7x+7y=56$
Because Sam gets double his pocket money in the week his granny's visit, Sam and Ben have a total of 91 dollars at the end of this week. This gives us the second equation:
$7(2x)+7y=91$ or simplified:
$14x+7y=91$.
How can we solve this system of equations?
- We subtract one of the equations from the other to eliminate one variable.
- We solve this equation using opposite operations.
- We plug this solution into any equation to get the solution of the second variable.
$\begin{align*} 7x+7y&=56\\ 14x+7y&=91. \end{align*}$
- Subtracting the equations $\rightarrow$ $7x=35$.
- Divide by $7$ $\rightarrow$ $x=5$.
- Substitute $x=5$ into $7x+7y=56$:
Now we divide by $7$ and get the solution:
$y=3$.
So, for a normal week, Sam gets a daily pocket money of 5 dollars, and Ben gets a daily pocket money of 3 dollars.
-
Establish a system of equations for the given situation.
HintsIf you have 4 cats and 5 dogs, you have 9 animals in total.
Remember: Usually you need as many equations as the number of variables.
SolutionFirst, we have to write a system of equations with the given information.
We assign $x$ to the number of containers of sample A, and $y$ to the number of containers of sample B.
The total number of containers is 25. This gives us the first equation:
$x+y=25$
Next consider the weight of each container:
- The maximum weight limit is 115 tons
- $x$ containers of sample A have a weigh 3 tons each
- $y$ containers of sample B have a weigh 7 tons each
$3x+7y=115$
Therefore, the system of equations is:
$\begin{align*} x+y&=25\\ 3x+7y&=115 \end{align*}$
-
Solve the system of equations by elimination.
HintsIt doesn't matter, which variable you eliminate. The solution is the same.
It's possible to eliminate one variable by multiplying only one equation.
If the coefficients of one variable are the same with different signs, you can add the equations. This way you'll get one equation with one variable.
You can solve this equation by using opposite operations:
The opposite operation of multiplication is division, and vice versa.
SolutionLet's have a look at the coefficients: $8$ and $4$ for $x$, and $13$ and $-4$ for $y$.
You can eliminate either $x$ or $y$. Because $8$ is $2\times 4$ it's easier to eliminate $x$. Therefore, we multiply the second equation by $-2$:
$\begin{align*} 8x+13y&=55\\ -2\times(4x-4y)&=-2\times(-4) \end{align*}$
Using the Distributive Property we get
$\begin{align*} 8x+13y&=55\\ -8x+8y&=8 \end{align*}$
Now we add the equations and get:
$21y=63$
Dividing by $21$ gives us the solution for $y$:
$y=3$
Now we plug this value into any of the original equations, for example $8x+13y=55$:
$\begin{array}{rcr} 8x+13\times 3&=&55\\ 8x+39&=&55\\ \color{#669900}{-39}&&\color{#669900}{-39}\\ 8x&=&16 \end{array}$
There is only one step left: We divide by $8$ and get the solution for $x$:
$x=2$
















