Solving Problems with Equivalent Ratios


Basics on the topic Solving Problems with Equivalent Ratios
After this lesson, you will be able to visually solve real-world problems with equivalent ratios using tape diagrams.
The lesson begins by teaching you that ratio problems can be visualized and solved using tape diagrams. It leads you to learn how to solve ratio problems using tape diagrams and find the value of each piece of tape. It concludes with noting that visual representations can be efficient when solving problems with equivalent ratios.
Learn about solving ratio problems by helping Paul give the best care possible to his plant.
This video includes key concepts, notation, and vocabulary such as ratio (a relationship between two non-negative numbers, both of which are not zero); a tape diagram (a visual representation of a ratio); and equivalent ratios (two ratios that are equal).
Before watching this video, you should already be familiar with ratios and how to represent them visually using tape diagrams.
After watching this video, you will be prepared to learn how to solve unit rate problems, including those involving unit pricing and speed; how to find a percent of a quantity as a rate per 100; and how to use ratio reasoning to convert measurement units.
Common Core Standard(s) in focus: 6.RP.A.1 and 6.RP.A.3 A video intended for math students in the 6th grade Recommended for students who are 11 - 12 years old
Transcript Solving Problems with Equivalent Ratios
Today we're visiting Paul's plant shop.
Paul loves and cares for all his plants, but he has a particular affinity for his Dionaea muscipula, aka, his venus fly trap.
This is because his venus fly trap, affectionately named Deon, wave hello, Deon, is a little plant with dreams of being a Broadway star.
To give Deon the best care possible, Paul needs to solve problems with equivalent ratios.
Deon, like all venus fly traps, needs a specific amount of light each day.
1 hour of light to 2 hours of darkness is the ideal ratio for Deon.
We can represent this visually with a tape diagram that shows the parts of the ratio.
Notice the one rectangle of light to two rectangles of darkness.
With the tape diagram the ratio always remains the same.
Therefore, using equivalent ratios, we can find out the number of hours of light that Deon needs per day.
We all know there are 24 hours in a day, so during a 24-hour period, how long should Deon be exposed to light and how long should he spend in darkness?
To find this solution, we divide the total hours, 24, by the total number of rectangles in the tape diagram.
In this case, 3.
Therefore, each rectangle represents 8 hours.
This shows that, each day, Deon needs 8 hours of light and 16 hours of darkness.
Wow! Looks like that sunlight has been good for Deon.
To keep growing strong he needs some really good soil.
Using a tape diagram, we can represent the soil mixture ideal for venus fly traps.
Deon's soil should contain 5 parts peat moss, 3 parts silica sand, and 2 parts perlite.
We need to know how much of each part of the soil will fit in Deon's 20-gallon flower pot.
To solve we should count the total number of rectangles.
There are 10 total rectangles.
Dividing we see that each rectangle represents 2 gallons.
Looks like we need 10 gallons of peat moss, 6 gallons of silica sand, and 4 gallons of perlite to fit the 20 gallon flower pot.
Only the best for Deon!
What nutrients Deon doesn't get through light and soil, he makes up for by trapping insects.
For every 3 flies Deon catches, he eats 7 ants.
This fall, Deon ate 48 more ants than flies.
How many of each insect did he eat?
This problem is a little bit different because we don't know how many insects Deon ate in total, but don't worry, we'll figure it out!
We know that Deon ate 48 MORE ants than flies.
The tape diagram for ants is 4 rectangles longer than the tape diagram for flies.
So, these 4 more rectangles must represent the 48 MORE ants!
To find the value of each rectangle, we divide the 48 by 4, and find that each rectangle equals 12 insects.
Which means Deon ate 84 ants and 36 flies this fall.
Is that right?
Let's check.
84 minus 36 is 48
So there were 48 more ants.
Too bad Deon's diet doesn't include breath mints.
There are a few steps we should summarize about solving problems with equivalent ratios.
First, create a tape diagram with given ratio.
Tape diagrams help us visualize and solve ratios problems.
Tape diagrams show the rectangles, or units, in a ratio and help us figure out their numeric value.
If you know the overall total, like the 24 hours in the light example, divide this number by the total number of rectangles, to find the value of each rectangle.
This gives us the solution for each part of the ratio.
We use the same steps of creating a tape diagram from given information.
Except, if you know the difference between two quantities in a ratio, like the 48 more ants than flies, count how many MORE rectangles one tape diagram has compared to the other.
Then, divide the difference between the quantities by the difference in the number of rectangles to find the value of each rectangle.
This, again, gives us the solution for each part of the ratio.
Paul has taken great care of Deon.
Therefore, Deon has been able to develop quite an impressive vocal range!
He's packed his bags and is off to Broadway.
Solving Problems with Equivalent Ratios exercise
-
Use tape diagrams and equivalent ratios to solve problems.
HintsGiven the ratio between different quantities and the total number of those quantities combined, we can use tape diagrams to find out how much of each quantity we have.
For example:
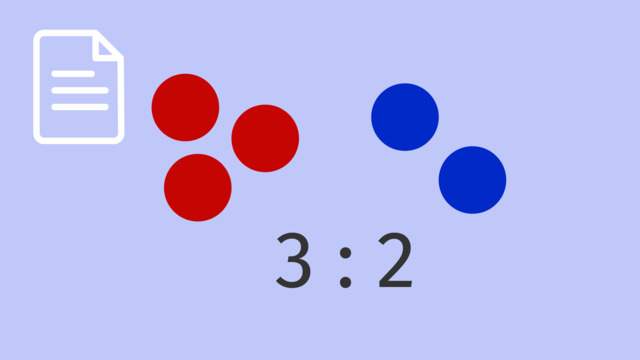
- Suppose we are given the ratio of Peanuts to Walnuts: $P:W=3:2$.
- We are also given a total of $P+W=30$ nuts in total.
- We know there are $3+2=5$ rectangles in total.
- That means each rectangle represents $\frac{30}{5}=6$ nuts.
- Since Peanuts have $3$ rectangles, there are $3\times6=18$ Peanuts.
- Since Walnuts have $2$ rectangles, there are $2\times6=12$ Walnuts.
We can use tape diagrams to solve problems involving three quantities. Suppose that in a restaurant, the ratio of Chairs to Tables to Stools is $3:2:1$. And suppose there are $42$ pieces of furniture total. How many of each type of furniture are in the restaurant?
- There are $6$ total rectangles.
- $\frac{42}{6}$ gives us $7$ pieces of furniture per rectangle.
- The number of Chairs is $3\times7=21$.
- The number of Tables is $2\times7=14$.
- The number of Stools is $1\times7=7$.
- We can check our answer by adding: $21+14+7=42$ pieces of furniture.
Given a ratio of quantities and a total number of those quantities:
- Draw rectangles to represent the ratio between different quantities.
- Find the total number of rectangles.
- Divide the total of the quantities by the total rectangles to get the quantity per rectangle.
- Then multiply to find how much of each quantity you've got.
SolutionBecause the ratio $P:C:D$ is $5:2:3$ , Phalaenopsis gets $5$ rectangles, Cattleya gets $2$, and Dendrobium gets $3$. There are $10$ rectangles in total. Because there are $100$ orchids in the shop, we divide $100$ by $10$ to give us $10$ orchids per rectangle. Because Phalaenopsis has $5$ rectangles, there are $5\times10=50$ plants of this type. Because Cattleya has $2$ rectangles, there are $2\times10=20$ plants of this type. Dendrobium has $3$ rectangles and so there are $3\times10=30$ plants of this type.
-
Use tape diagrams to solve the given ratio problem.
HintsGiven a ratio, we can determine how many more rectangles are assigned to one quantity over another.
For example:
- Suppose we are give that the ratio of Cars to Trucks at a car dealership is $C:R=14:11$.
- We are also given that there are $12$ more Cars than Trucks.
- Cars have $14$ rectangles and Trucks have $11$.
- Cars have $14-11=3$ more rectangles than Trucks.
- Because there are $12$ more Cars than Trucks and that's represented by $3$ rectangles, each rectangle represents $\frac{12}{3}=4$ automobiles.
- So there are $14\times4=56$ Cars and $11\times4=44$ Trucks.
- We can confirm our answer by subtracting the number of Trucks from the number of Cars: $56-44=12$.
Given a ratio and the difference between the quantities, we can find the amount of each quantity:
- Assign rectangles to each quantity based on the given ratio.
- Subtract the number of rectangles of one quantity from that of the other.
- Divide the given difference between the quantities by the number of rectangles from the last step. This gives you the quantity per rectangle.
- Multiply the number of rectangles for each quantity times the quantity per rectangle to get the value for each quantity.
Suppose the ratio of a quantity $A$ to a quantity $B$ is $8:5$, and the difference $A-B=30$. What's quantity of $A$ and the quantity of $B$?
- $8-5=3$.
- $\frac{30}{3}=10$.
- The quantity of $A$ is $8\times10=80$.
- The quantity of $B$ is $5\times10=50$.
- We can check our answer: $80-50=30$, the difference given in the original problem.
SolutionGiven:
- The ratio of Blueberries to Raspberries is $4$ to $7$.
- There are $27$ more Raspberries than Blueberries.
- Write the ratio in proper notation:
- $B:R=4:7$.
- Subtract to find the difference in the number of rectangles assigned to each quantity:
- $7-4=3$.
- Divide to find the number of berries per rectangle:
- $\frac{27}{3}=9$ berries per rectangle.
- Multiply to find the number of Blueberries and Raspberries:
- $4\times9=36$ Blueberries, and $7\times9=63$ Raspberries.
- Subtract these values to check your answer:
- $63-36=27$.
-
Determine the total number of Venus fly traps and roses in Paul's shop.
HintsSuppose the ratio of Road Bikes to Mountain Bikes in a bike shop is $R:M=5:7$, and there are 12 more Mountain bikes than Road bikes in the shop.
- The tape diagram will show $2$ more rectangles for $M$ than $R$.
- Those $2$ rectangles represent $12$ bikes.
- So each rectangle represents $\frac{12}{2}=6$ bikes.
- Because we have $5+7=12$ rectangles, we have $12\times6=72$ bikes in total.
Suppose the ratio of Burritos to Tacos at a Mexican food truck is given as $B:T=5:9$, and there are $20$ more Tacos than Burritos.
- The tape diagram will show $4$ more rectangles for $T$ than $B$.
- Those $4$ rectangles represent $20$ food items.
- So each rectangle represents $\frac{20}{4}=5$ food items.
- Because we have $5+9=14$ rectangles, we have $14\times5=70$ food items in total.
SolutionAt Paul’s plant shop there are $5$ Venus Fly Traps for every $8$ Roses. Paul has $90$ more Roses than Venus Fly Traps. How many Venus Fly Traps and Roses does Paul’s plant shop have?
- The ratio of Venus Fly Traps to Roses is given as $V:R=5:8$.
- The tape diagram has $8$ rectangles on top and $5$ on the bottom, so the top represents Roses and the bottom represents Venus Fly Traps.
- There are $3$ more rectangles for Roses than for Venus Fly Traps.
- Those $3$ rectangles represent $90$ plants.
- So each rectangle represents $\frac{90}{3}=30$ plants.
- There are $5+8=13$ rectangles in total, so there are $13\times30=390$ plants in total.
-
Calculate the solution to the following problems using tape diagrams.
HintsSuppose the ratio of Planets to Moons around a star is $11:14$. There are $100$ celestial bodies in total associated with the star. How many more Moons than Planets are there?
- All the celestial bodies are represented by $25$ rectangles.
- Each rectangle represents $\frac{100}{25}=4$ celestial bodies.
- There are $14-11=3$ more rectangles for Moons than for Planets.
- Those $3$ rectangles represent $3\times4=12$ Moons.
Suppose the ratio of Football teams to Basketball teams in a town is $4$ to $5$. There are $3$ more Basketball teams than Football teams. How many teams are there in total?
- The difference in rectangles is $1$.
- This rectangle represents $3$ teams.
- There are $4+5=9$ rectangles in total.
- There are $9\times3=27$ teams in total.
Suppose the ratio of Plates to Cups in a kitchen is $7$ to $10$, and there are $12$ more Cups than Plates. How many Plates are there?
- There are $10-7=3$ more rectangles for Cups than Plates.
- Those $3$ rectangles represent $12$ pieces of dinnerware.
- Each rectangle represents $\frac{12}{3}=4$ pieces of dinnerware.
- There are $7 \times 4=28$ Plates.
SolutionA clothing store features Shirts and Pants in the ratio of $3:6$. There are $42$ more Shirts than pairs of Pants. How many articles of clothing in total are in the store?
- $6-3=3$ more rectangles for Shirts than Pants.
- $\frac{42}{3}=14$ articles of clothing per rectangle.
- $3+6=9$ rectangles in total.
- $9\times 14 =126$ articles of clothing in the store.
- $11-7=4$ more rectangles for Cubist works.
- $\frac{24}{4}=6$ works of art per rectangle.
- $7 \times 6 = 42$ Impressionist works.
- There is $1$ more rectangle for Raisins than Peanuts.
- This rectangle represents $2$ Raisins.
- There are $10\times2=20$ Raisins in total.
- There are $9+7=16$ rectangles in total.
- These rectangles represent $32$ songs in total.
- Each rectangle represents $\frac{32}{16}=2$ songs.
- There are $9-7=2$ more rectangles for the Eighties than the Nineties.
- That represents $2\times2=4$ songs.
-
Create a tape diagram to represent the given ratios.
HintsIf the ratio $A:B=25:10$, we can reduce this ratio by dividing each value by $5$:
- $\frac{25}{5}=5$
- $\frac{10}{5}=2$
If the ratio $A:B=7:3$, we can say that the ratio $B:A=3:7$.
Given the following ratios, we can combine them into a single ratio statement involving three values:
- $A:B=5:7$
- $B:C=7:4$
- Therefore: $A:B:C=5:7:4$
SolutionThe given ratios are $P:M=12:8$ and $T:M=15:30$.
- $P:M=12:8$ can be reduced.
- Dividing each value by $4$ gives us $P:M=3:2$.
- $T:M=15:30$ can also be reduced.
- Dividing each value by $2$ gives us $T:M=1:2$.
- If $T:M=1:2$, then $M:T=2:1$.
- Therefore, $P:M:T=3:2:1$.
- In the tape diagram, $P$ gets $3$ rectangles, $M$ gets $2$, and $T$ gets $1$.
-
Confirm or correct the solution to each word problem.
HintsRemember, with ratios, order matters. If the ratio of Cups to Bowls is $3:10$, we must be careful to assign $3$ rectangles to Cups, and $10$ rectangles to Bowls, not the other way around.
Remember, we have used two different methods to find the quantity per rectangle:
- Given $A:B=2:7$,
- And there are $45$ more of $A$ than $B$, we compute:
- $\frac{45}{5}=9$ units per rectangle.
- Given $A:B=2:7$,
- And there are $45$ units in total, we compute:
- $\frac{45}{9}=5$ units per rectangle.
If we can find the values of two quantities, we can compute a reduced ratio between them. For example:
- Given $A=400$ and $B=1400$,
- $A:B=400:1400$.
- We can reduce this by dividing each value by $200$:
- $A:B=2:7$
SolutionA scout troop is selling boxes of cookies. The ratio of boxes of Chocolate Chip to boxes of Sugar cookies is $5$ to $6$. There are $33$ boxes of cookies in total. Chocolate Chip cookies are represented by $5$ rectangles, and Sugar by $6$ rectangles. There are $\frac{33}{11}=3$ boxes per rectangle. This gives us $5\times 3=15$ boxes of Chocolate Chip, and $6\times 3=18$ boxes of Sugar cookies.
A grove of trees has Spruce trees and Fir trees such that $S:F=6:3$. There are $90$ more Spruce trees than Fir trees. There are $3$ more rectangles for Spruce than for Fir. So there are $\frac{90}{3}=30$ trees per rectangle. That means there are $6\times30=180$ Spruce trees and $3\times30=90$ Fir trees.
A fruit table at a marathon features Apples, Oranges, and Bananas. There are $48$ more Bananas than Oranges. The ratio $O:B=6:8$. There are $264$ Apples and Oranges. What is the ratio of Apples to Oranges?
There are $2$ more rectangles for Bananas than for Oranges. This means there are $\frac{48}{2}=24$ pieces of fruit per rectangle. There are $6$ rectangles for Oranges, so there are $6\times 24=144$ Oranges. Since there are $264$ Apples and Oranges, there must be $264-144=120$ Apples. The ratio of Apples to Oranges is $120:144$ which reduces to $5:6$.