What is a Ratio? (Using Ratio Language)
Learning text on the topic What is a Ratio? (Using Ratio Language)
Understanding Ratios
Ratios are a fundamental part of mathematics and are used in many different areas, including cooking, map reading, and even in your favorite video games. If you're curious about how ratios are everywhere in our lives, you're in the right place! Let's explore what ratios are, the terminology used with them, and how we can understand them better. Get ready to dive into the world of ratios!
What is a Ratio?
A ratio is a way to compare two quantities by showing how many times one value contains the other. It tells us about the relative size of two quantities. Think of it like a recipe - if a cake recipe calls for 2 cups of flour and 1 cup of sugar, we can say the ratio of flour to sugar is 2:1.
Key Terms in Ratios
Here are some important terms you'll come across when learning about ratios:
| Term | Definition |
|---|---|
| Antecedent | The first number in a ratio |
| Consequent | The second number in a ratio |
| Equivalent Ratios | Different ratios that express the same relationship |
| Proportion | An equation stating that two ratios are equal |
Examples of Ratios
If a bag has 6 red marbles and 4 blue marbles, the ratio of red to blue marbles is 6:4.
In a classroom with 10 girls and 15 boys, the ratio of girls to boys is 10:15.
Ratio Language – Different Expressions
Ratios can be expressed in different ways:
- As a fraction: $\frac{1}{2}$
- Using a colon: 1:2
- With the word 'to': 1 to 2
All these expressions mean the same thing - for every 1 of the first quantity, there are 2 of the second quantity.
Ratio– Application
Answer these questions to test your understanding of ratios and the terms used in ratios.
What is a Ratio?– Summary
Key Learnings from this Text:
A ratio is a comparison of two quantities.
Ratios can be written in different forms but mean the same thing.
Understanding the terms like antecedent, consequent, equivalent ratios, and proportion is crucial.
Ratios are used in everyday life in various ways.
Keep practicing with ratios in different scenarios to strengthen your understanding. Make sure you are using the ratio terminology that you have learned today. If you are ready to do some ratio-related math, apply it to calculating lengths. And remember, ratios are not just numbers; they are a way to understand the world around us!
##What is a Ratio?– Frequently Asked Questions
What is a Ratio? (Using Ratio Language) exercise
-
Defining the keywords of ratios.
HintsIn the ratio $a : b$ the $a$ is the antecedent.
In the ratio $a : b$ the $b$ is the consequent.
The ratio $6:4$ can be simplified to $3:2$ by dividing both sides by 2. Both ratios represent the same proportion, indicating equivalence.
SolutionHere are the correct matching keywords and definition pairs
- Antecedent - The first number in a ratio
- Consequent - The second number in a ratio
- Equivalent Ratios - Different ratios that express the same relationship
- Proportion - An equation stating that two ratios are equal
-
Use ratio notation to represent a data set.
HintsHow many blue counters are there? How many red counters are there?
Does the question prioritise the count of the blue or the red counters in the proportion? The order in the question determines the order in your ratio response.
Ratio describes the relationship between quantities, highlighting how one quantity compares to another. In this context, we're focusing on the number of blue counters in relation to the number of red counters.
The number of blue counters should come first in the ratio and is called the antecedent. The number of red counters should come second in the ratio and is called the consequent.
SolutionThe correct answer is $10:6$. This is because there are 10 blue counters and 6 red counters. When writing a ratio, the first quantity given in the question goes first in the ratio notation. Hence why the ratio is $10:6$ in that order.
-
Ratios from Pictures
HintsThe text underneath the pictures is the order the ratio should be in.
Count all of one item in the picture and then count all of the other item in the picture. Write these amounts as a ratio now using the : symbol.
You may need to simplify a ratio to find its matching answer. These are called equivalent ratios and can easily be found my multiplying or dividing, often by a whole number like 2, 3 or 4.
The ratio of cupcakes to ice creams in the image is initially 4:10. Dividing both sides of the ratio by 2 results in the simplified ratio of 2:5.
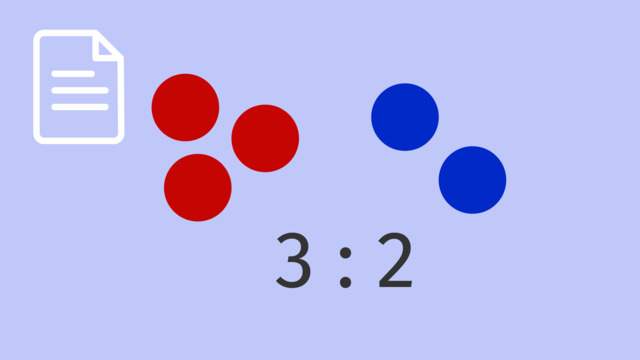
Solution- In the picture containing balloons, there are 3 red and 2 blue. This can be written as the ratio $3:2$.
- In the picture containing pencils, there are 14 orange pencils and 2 green pencils. This can be written as the ratio $14:2$ but can be simplified to the equivalent ratio of $7:1$.
- In the picture containing apples and bananas, there is 1 apple and 4 bananas. This can be written as the ratio $1:4$.
- In the picture containing stars and moons, there are 4 stars and 6 crescent moons. This can be written as the ratio $4:6$ which can be simplified to the equivalent ratio of $2:3$.
- In the picture containing footballs and tennis balls, there are 3 footballs and 5 tennis balls. This can be written as the ratio $3:5$.
-
Equivalent Ratios
HintsEquivalent ratios are ratios that express the same relationship between two quantities but may have different absolute values. In other words, they represent the same proportion or comparison, but the numbers involved may vary.
Try multiplying or dividing the ratios by simple numbers like 2, 3 or 4 to gain equivalent ratios.
Two equivalent ratios are 5:1 and 10:2. This equivalence arises because both parts of the ratio 5:1 are multiplied by 2, resulting in the ratio 10:2.
SolutionThe ratios which are equivalent to $2:3$ are $4:6$, $6:9$ and $8:12$
The ratios which are equivalent to $4:3$ are $8:6$, $12:9$ and $16:12$.
The ratios which are equivalent to $2:1$ are $4:2$, $6:3$ and $8:4$.
-
What is the ratio of apples to oranges?
HintsHow many apples are there? How many oranges are there?
The question asks for the ratio of apples to oranges so make sure the number of apples comes first in your ratio.
The ratio of cupcakes to ice creams is $4:10$. This can be simplified by dividing both sides of the ratio by $2$ to give a simplified ratio of $2:5$.
SolutionThe correct answer is $6:4$. This is because there are 6 apples and 4 oranges. When writing a ratio, the first quantity given in the question goes first in the ratio notation. Hence why the ratio is $6:4$ in that order.
-
Alternative Forms for Ratios
HintsThe correct notation for use with ratios is to use a colon sign (:).
Equivalent ratios are in the same order of portions. For example, the ratio $4:3$ is equivalent to the ratio $8:6$ but not the ratio $6:8$.
When writing ratios as fractions, the first number in the ratio (the antecedent) is the numerator of the fraction and the second number in the ratio (the consequent) is the denominator in the fraction.
SolutionThe correct full text that Luke should have been given should say the following. Corrections have been highlighted in bold.
A ratio represents a comparison between two quantities, indicating how many times one quantity is contained within another.
It is expressed as a relationship between two numbers, separated by a colon (:), such as 2:3.
Ratios can be equivalent if they represent the same relationship between quantities. To find equivalent ratios, you can multiply or divide both parts of the ratio by the same non-zero number.
For instance, the ratio 2:3 is equivalent to 4:6, 6:9, and so on, as long as both parts of the ratio are multiplied or divided by the same number.
Ratios can also be represented as fractions, where the first number in the ratio is the numerator and the second number is the denominator. For example, the ratio 2:3 can be written as the fraction $\frac{2}{3}$.
Ratios can also be represented using the word 'to'. For example, the ratio 5:1 can also be written as 5 to 1.