Solving One-Step Inequalities by Multiplying or Dividing
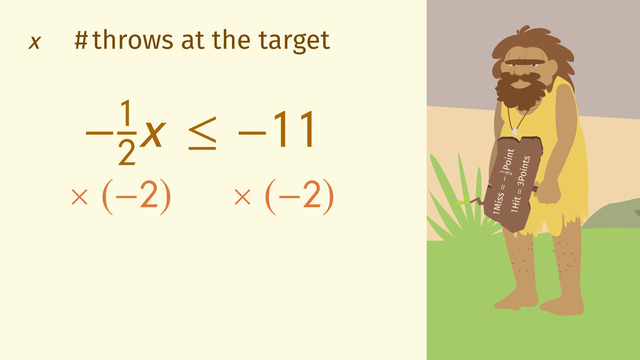

Basics on the topic Solving One-Step Inequalities by Multiplying or Dividing
For simple inequalities such as x < 5, we know all the values less than 5 are in the solution set. But, what if there is a coefficient to the variable such as with this inequality: 2x > 10. This is a one-step inequality problem, and we can solve this type of inequality problem by using the inverse of multiplication or division.
If a coefficient is multiplied with the variable, isolate the variable by dividing by the coefficient on both sides of the equation. If the coefficient divides the variable, isolate the unknown value by multiplying by the coefficient on both sides of the equation. Always, keep the inequality balanced. Whatever you do to one side of the sign you must do to the other side. Unlike solving one-step inequalities by addition and subtraction, for multiplication and division problems, you must also consider the direction of the inequality sign.
Remember the rule, if multiplying or dividing by a positive number, maintain the direction of the sign. When multiplying or dividing by a negative number, flip the sign over, so it points in the opposite direction.
It’s a good idea to check you work, to catch any careless errors you might make such as forgetting to flip the inequality sign. When graphing on the number line, an open dot is for greater than (>) and less than (<) and a closed dot represents inequalities of more than and equal to (≥) and less than and equal to (≤). To learn more about one-step inequalities by multiplying or dividing, watch this video. You will flip over our characters.
Use inequalities to solve problems. CCSS.MATH.CONTENT.HSA.CED.A.3
Transcript Solving One-Step Inequalities by Multiplying or Dividing
To learn how to solve one-step inequalities with multiplication and division, let’s go back in time.
Look! Two cavemen are eating dinner. Seems like they're just about finished! Look at all those bones!
One of the cavemen picks up a bone and throws it. He hits a rock. What fun! The cavemen decide to make a game of it and throw the bones for points. First, they agree on the rules.
One-Step Inequality Example Calculation 1
Each hit on the bullseye is worth 3 points and a loss of half of a point for each miss. This caveman has 12 Points. Since we don't know the number of times he hit the bullseye, we'll let the variable x represent this quantity.
Each time the cavemen hit the bullseye is worth 3 points. If there were no misses, 3x would equal 12. But since we know that every miss costs the cavement precious points. So it's possible that the cavemen missed the target on a few throws.
Let's write an inequality: 3x ≥ 12.
To solve the inequality, divide each side by 3: x ≥ 4. To have a score of 12, the caveman could have hit the bullseye 4 or more times.
One-Step Inequality Example Calculation 2
Here's the second contender. Oh man! The second caveman's score is minus 11 points.
If the second caveman didn't hit the target a single time, negative 1/2 x would equal minus 11, where x is the number of throws. But his total number of throws might be higher if he was successful at hitting the target on occassion. So, −1/2 · x ≤ −11.
To solve the inequality, divide both sides by negative one-half which is the same as multiplying both sides by the inverse of negative one-half which is negative two.
Since you are multiplying or dividing by a negative number, don’t forget you have to flip the inequality sign.
x is greater than or equal to 22. He could have made 22 or more attempts! This caveman is a persistent fellow! He should get extra credit for effort!
Why flip the Inequality Sign?
But when we multiply or divide with a negative number, why do we flip the inequality? To flip or not to flip, that is the question.
Let's look at another example. Negative two is less than five. Watch what happens when we divide both sides by negative 1, but this time, we won't flip the inequality. −2 ÷ −1 < 5 ÷ −1. So we get 2 < −5!
2 < −5? That’s not right. But, if we flip the sign, like we were supposed to, then we get a true inequality. So remember:
When you multiply or divide an inequality by a negative number, you must flip the inequality sign.
There they go again! They're really persistent! Hooray, he got one! He hit the bullseye! Oh no! That's not a rock! Run cavemen! Run!
Solving One-Step Inequalities by Multiplying or Dividing exercise
-
Explain the rules of the cavemen's game.
HintsThink about all the signs that can be flipped.
Does it make sense to flip the equal sign?
For the inequality $-2x \le 8$, look what happens when we isolate the variable $x$.
$\begin{array}{rcrcl} -2x &\le& 8\\ \color{#669900}{\div(-2)}&&\color{#669900}{\div(-2)}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&\ge&-4&&|\text{ Look what happened to the Inequality Sign!} \end{array}$
Do you see the problem? Which operation did we perform?
$\begin{array}{rcr} -2 &~~<& 5\\ \color{#669900}{\times (-1)} &~~~& \color{#669900}{\times (-1)}\\ 2 &~~<& -5 \end{array}$
SolutionWhen solving inequalities you must pay special attention to the inequality sign.
But don't worry and just remember: When you multiply or divide an inequality by a negative number, you must flip the inequality sign.
To see how it works, let's solve this inequality:
$\begin{array}{rcr} -2 &~~<& 5\\ \color{#669900}{\times (-1)} &~~~& \color{#669900}{\times (-1)}\\ 2 &~~>& -5 \end{array}$
As you can see, the multiplication of a negative number calls for a flip of the inequality sign. Otherwise the result would be $2<-5$, which is not correct.
-
Calculate the number of times at least the first cavemen hit the bullseye.
HintsWhen calculating with inequalities, remember that the solution set also includes numbers greater than or less than the final solution.
The inequality $-2 < x$ has an infinite number of solutions. There are countless integers larger than $-2$.
SolutionLet's take a deeper look at the score of the first cavemen - who has $12$ points.
What does this score mean to us? Since we don't know the play-by-play of the game, we will have to make some assumptions:
- If we assume the caveman never missed the target, we can use the following equation: $3x =12$. The variable $x$ stands for the number of times the caveman hit the bullseye. We can solve this equation by dividing both sides by $3$. The solution is $x=4$. This means the caveman threw the bone four times and never once missed the target.
- If we assume the caveman had some misses as well, we can use the inequality $3x \ge 12$. If we by divide by $3$, we are left with $x \ge 4$. In this case the caveman hit the bullseye four or more times.
-
Analyze the scores of the cavemen's friends.
HintsPay attention, and read the problem carefully. To figure out the number of attempts, depending if the caveman had any hits at all, you may use an equation or an inequality.
To solve this equation, see how we flip the inequality sign when we multiply by a negative number?
\begin{array}{rcr} -\frac12 x &~~\le& -5\\ \color{#669900}{\times (-2)} &~~~& \color{#669900}{\times (-2)}\\ x &~~\ge& 10 \end{array}
SolutionThese cavemen don't really seem to be that good at throwing. Each has a negative score! What conclusions can we draw from the results of their competition?
- With a score of $-4$ points, we can write the equation $- \frac12 x \le -4$. Dividing by $-\frac12$ means multiplying by $(-2)$. We must remember to flip the inequality sign. Now we get $x \ge 8$. So this caveman had at least $8$ throws.
- Another caveman had a score of $-7$ points. Since he had no successful throws, our equation is $-\frac12 x = -7$. Multiplying both sides by $(-2)$ gives us $x=14$. This caveman had exactly $14$ throws since he never hit the bullseye.
- Another not-very-talented caveman has a score of $-2$. Calculating as before, we transform our inequality, $-\frac12 x \le -2$, to $x \ge 4$. This caveman had at least four throws.
- The last caveman had the best score of $-1$. This means he had at least two throws.
-
Decide which sign has to be flipped to solve the inequality.
HintsOur goal is to isolate $x$. This way, we are able to define the solution set of $x$.
SolutionRemember, when multiplying or dividing an inequality by a negative number, flip the sign.
To solve these inequalities, flip the sign:
- $-3x<5$
- $-4x<-7$
- $-x \le 1$
- $-x \ge 0$
- $4x>-3$
- $2x \ge 0$
-
Define the meaning of each inequality sign.
HintsWhich inequality sign makes a true statement?
- $-2<5$
- $-2 > 5$
- $-2 \le 5$
- $-2 \ge 5$
When we introduce variables, we get even bigger solution sets.
Which numbers fulfill the inequality $x \le 5$?
SolutionThere are four inequality signs:
- $x<y$ meaning $x$ less than $y$
- $x>y$ meaning $x$ greater than $y$
- $x\le y$ meaning $x$ less or equal to $y$
- $x\ge y$ meaning $x$ greater or equal to $y$
-
Calculate the inequality $-2x-2 \ge (-2x+1) \times 4$.
HintsWhen you multiply or divide an inequality by an negative number, you must flip the inequality sign.
SolutionTo solve this problem, there is more than one way to combine like terms. For the method shown here, the sign does not flip, but there is an alternative sequence of steps that results in flipping the sign:
Beginning with row $3$ we could have transformed $-2x \ge -8x+6$ to $-6 \ge -6x$. Then we would have divided by $-6$ getting $1 \le x$, which is the same answer.















nice
COOL