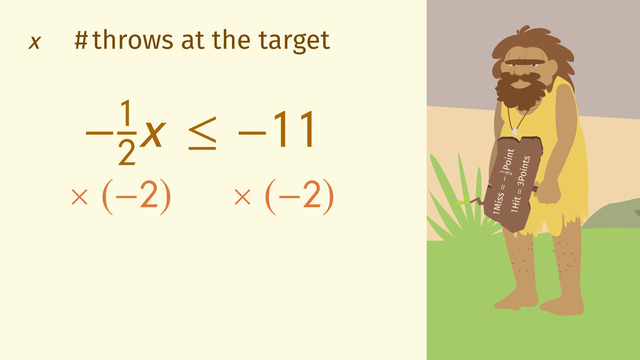Solving Multi-Step Inequalities
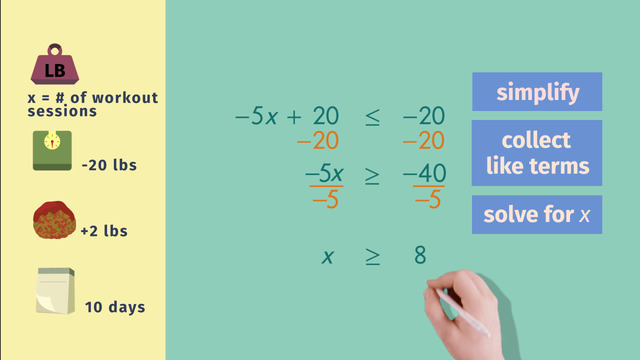

Basics on the topic Solving Multi-Step Inequalities
Just like equations, inequality problems can require multiple steps to calculate the answer. The steps to solve multi-step inequality problems start out the same as the steps to solve multi-step equations.
First, if parentheses are used in the problem, simplify those terms. Use the Distributive Property if needed. Next step, collect the like terms by adding and subtracting. After that, solve for the variable using opposite operations. This all seems the same – but watch out. The difference is the inequality sign. Your last step in solving the problem is to attend to the inequality sign.
To solve for the variable, if you multiplied or divided by a negative number, you must flip the inequality sign, so it points in the opposite direction. In other words, if you multiply or divide by a negative number, greater than (>) becomes less than (<), and less than becomes greater than. The same goes for the greater than and equal to (≥) and less than and equal to (≤) symbols.
Don’t forget to check your work. It’s always important to check your work but especially when there are many steps because the more work you do – the greater the chance of making a careless error. To learn more about multi-step inequalities and how and when to flip the symbol, press play to start this video.
Use inequalities to solve problems. CCSS.MATH.CONTENT.HSA.CED.A.3
Transcript Solving Multi-Step Inequalities
Rocky is watching television while eating his favorite food, meatballs, when suddenly...This could be the perfect opportunity for Rocky's great comeback. To figure out how he can get back into shape, we can use solving multi-step inequalities. He remembers the good 'ol days when he was fit and won the beauty contest. He has to get in shape in ten days. This requires a call to his former coach.
Rocky won competitions at a weight of 50 pounds. He knows from his old workout schedule that he loses five pounds during a workout session. He has gained a lot of weight and now weighs seventy pounds. Therefore, he has to lose twenty pounds in ten days to reach his former weight. But, he loves his meatballs and has to eat meatballs daily, so he still gains two pounds a day in meatball weight.
The minimum
We want to know the minimum number of workout sessions Rocky needs to lose twenty or more pounds. Let's look at the facts: he loses five pounds each session. Let's let x stand for the number of workout sessions. Rocky gains two pounds a day for 10 days. In the end, he wants to lose 20 or more pounds. So we put an equal to or less than sign in between.
multiplying and subtracting
Simplify the value inside of the parenthesis by multiplying. Then, collect like terms. Apply the opposite operation to move the twenty to the right side of the inequality. This can be accomplished by subtracting twenty on both sides of the inequality. Now we can solve for x. Again, apply the opposite operation to eliminate the negative five in front of the x. This can be accomplished by dividing both sides of the inequality by negative five.
Be careful: The inequality sign is reversed each time we divide by a negative number. The result is X is greater than or equal to eight. So, he starts training. Now that Rocky has had eight training sessions, let's check on his progress. Substitute X in the equation with the number eight. Simplify the left side of the inequality by multiplying.
solve the Multi-Step inequality
Then, complete the addition on the left side of the inequality. If Rocky has eight training sessions, he will definitely reach his goal! But what if he trains more than that? Rocky has two more training sessions. To see what happens when Rocky has more training sessions, we can substitute X with ten - or any other number greater than 8.
As you can see, we get a true statement again, so if Rocky trains for more than 8 sessions, he will also reach his goal. Woohoo! Rocky won the competition! Let's have a look at his prize. His prize is meatballs for a lifetime. Poor Rocky, will he ever win another competition? Luckily, he still has his coach.
Solving Multi-Step Inequalities exercise
-
How to set up an inequality.
HintsThink about a way to represent the number of workout sessions.
For example:
- If Rocky does $4$ workout sessions during the $10$ days, he can loses $4\times 5$ pounds.
SolutionWhen Rocky won last year's beauty competition,he weighed 50 pounds. Just to qualify for this year's competition, he must lose at least $20$ pounds. He has $10$ days to lose the weight.
- He can lose $5$ pounds with each workout session. We can express this as $-5x$.
- Since Rocky eats $2$ lbs. of meatballs per day, we can write this as a constant: $2\times 10$.
- Because Rocky has to lose at least $20$ pounds, we use the $\le$ sign. So our answer, $x$, will be the minimum number of workout sessions needed to lose $20$ pounds.
-
Determine the number of workout sessions Rocky needs to reach his goal of losing $20$ pounds.
HintsYou can solve the inequality above just like you would solve an equation. First, combine like terms then use opposite operations to isolate the variable $x$.
Remember:
- If you multiply or divide an inequality by a negative number, you have to flip the inequality sign.
- ($\le~\longleftrightarrow~\ge$)
For example: The statement $2 \le 4$ is correct. If we multiply this statement by $-2$, we get $-4 \ge -8$.
SolutionLet's look at the given facts:
- Rocky loses $5$ pounds per workout session
- He also eats $2$ pounds of meatballs per day for $10$ days
- Rocky wants to lose at least $20$ pounds.
$~$
We can write the inequality: ($-5 = $ weight Rocky loses per workout session)($x= $ mumber of workout sessions) + (2 pounds of meatballs)(10 days) $\le$ ($-20 = $ Rocky's target weight loss)
$~$
$\begin{array}{rcll} -5x + (2 \times 10) &\le& -20& \\ -5x + 20 &\le& -20& \\ \color{#669900}{-20} && \color{#669900}{-20} &~~~~~|~ \text{Opposite Operations} \\ -5x &\le& -40 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 8 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
$~$
This means that Rocky should participate in at least eight workout sessions. Of course, he can also participate in more than eight sessions.
$~$
Let's check our work:
$8$ sessions:
$\begin{array}{rcll} -5(8) + 20 &\le& -20 &\\ -20 &\le& -20 &~~~~~\surd \end{array}$
$10$ sessions:
$\begin{array}{rcll} -5(10) + 20 &\le& -20 & \\ -50 + 20 &\le& -20 & \\ -30 &\le& -20 &~~~~~\surd \end{array}$
Go Rocky!
-
Decide how many workout sessions Bruno needs to complete.
HintsFirst, determine the inequality.
The inequality is: $-4x+(3\times 10)\le -10$.
Solve this inequality as follows:
- Simplify
- Combine Like Terms
- Solve for $x$
Remember, because you divide by a negative number across the inequality, the inequality sign has to change directon.
SolutionWhat do we know?
- Bruno loses $4$ pounds per workout session.
- Bruno eats $3$ pounds of meatballs per day for $10$ days.
- He wants to lose at least $10$ pounds.
$-4x+(3\times 10)\le -10$
$~$
$\begin{array}{rcll} -4x + (3 \times 10) &\le& -10& \\ -4x + 30 &\le& -10& \\ \color{#669900}{-30} && \color{#669900}{-30} &~~~~~|~ \text{Opposite Operations} \\ -4x &\le& -40 \\ \color{#669900}{\div{-4}} && \color{#669900}{\div{-4}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 10 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
To lose the amount of weight he wants, Bruno needs to complete at least $10$ workout sessions. Of course, if he enjoys it, he can do more than $10$ sessions.
Perhaps Rocky and Bruno should be workout partners!
-
Examine the effect of different diets on the Rocky's weight loss.
HintsFor the inequality, what is the unknown quantity?
$-5x+(?\times 10)\le -30$
The ? represent the amount of weight gained after eating each type of food.
Solve each inequality by
- Simplifying
- Combining like terms
- Solving for $x$ by using opposite operations
You can also check your answers by plugging the solution back into each inequality.
SolutionFor this problem set, to solve each inequality, the only change is the weight gain as a result of eating the different food options.
Salad
$\begin{array}{rcll} -5x + (0.5 \times 10) &\le& -30& \\ -5x + 5 &\le& -30& \\ \color{#669900}{-5} && \color{#669900}{-5} &~~~~~|~ \text{Opposite Operations} \\ -5x &\le& -35 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 7 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
$~$
Sausages
$\begin{array}{rcll} -5x + (1 \times 10) &\le& -30& \\ -5x + 10 &\le& -30& \\ \color{#669900}{-10} && \color{#669900}{-10} &~~~~~|~ \text{Opposite Operations} \\ -5x &\le& -40 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 8 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
$~$
Steak
$\begin{array}{rcll} -5x + (1.5 \times 10) &\le& -30& \\ -5x + 15 &\le& -30& \\ \color{#669900}{-15} && \color{#669900}{-15} &~~~~~|~ \text{Opposite Operations} \\ -5x &\le& -45 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 9 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
$~$
Meatballs
$\begin{array}{rcll} -5x + (2 \times 10) &\le& -30& \\ -5x + 20 &\le& -30& \\ \color{#669900}{-20} && \color{#669900}{-20} &~~~~~|~ \text{Opposite Operations} \\ -5x &\le& -50 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 10 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$
-
Describe the steps required to solve the inequality $-5x+(2\times5)\le -20$.
HintsUse opposite operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
Don't forget: when multiplying by or dividing by a negative number across an inequality, you have to remember to flip the inequality sign.
Solution$\begin{array}{rcll} -5x + (2 \times 10) &\le& -20& \\ -5x + 20 &\le& -20&~~~~~|~ \text{Simplify by Multiplying} \\ \color{#669900}{-20} && \color{#669900}{-20} &~~~~~|~ \text{Combine Like Terms using Opposite Operations} \\ -5x &\le& -40 \\ \color{#669900}{\div{-5}} && \color{#669900}{\div{-5}} &~~~~~|~ \text{Opposite Operations} \\ x &{\ge}& 8 &~~~~~|~ \text{Flip sign} \le~ \rightarrow ~\ge \text{because we divided by a negative number} \end{array}$
-
Solve the given inequalities.
HintsYou can solve each equation by:
- Simplifying
- Combining Like Terms
- Solving for $x$
Use the opposite operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
SolutionHow do we solve inequalities?
- First, we simplify, if it's necessary.
- Next, we Combine Like Terms using the Opposite Operations of addition or subtraction.
- Finally, we use Opposite Operations like multiplication or division to solve for $x$.
$\begin{array}{rcll} 4x + 4 &\ge& 12& \\ \color{#669900}{-4} && \color{#669900}{-4} &~~~~~|~ \text{Opposite Operations} \\ 4x &\ge& 8 \\ \color{#669900}{\div{4}} && \color{#669900}{\div{4}} &~~~~~|~ \text{Opposite Operations} \\ x &\ge& 2 & \end{array}$
$~$
$\begin{array}{rcll} -2x + (5 \times 3) &\ge& 5& \\ -2x + 15 &\ge& 5& \\ \color{#669900}{-15} && \color{#669900}{-15} &~~~~~|~ \text{Opposite Operations} \\ -2x &\ge& -10 \\ \color{#669900}{\div{-2}} && \color{#669900}{\div{-2}} &~~~~~|~ \text{Opposite Operations} \\ x &\color{#669900}{\le}& 5 &~~~~~|~ \text{Flip the sign} \ge~ \rightarrow ~\le \text{because we divide by a negative number} \end{array}$
$~$
$\begin{array}{rcll} 3x - (2 \times 4) &\le& 4& \\ 3x - 8 &\le& 4& \\ \color{#669900}{+8} && \color{#669900}{+8} &~~~~~|~ \text{Opposite Operations} \\ 3x &\le& 12 \\ \color{#669900}{\div{3}} && \color{#669900}{\div{3}} &~~~~~|~ \text{Opposite Operations} \\ x &\le& 4 \end{array}$
$~$
$\begin{array}{rcll} -6x - (3 \times 12) &\le& -60& \\ -6x - 36 &\le& -60& \\ \color{#669900}{+36} && \color{#669900}{+36} &~~~~~|~ \text{Opposite Operations} \\ -6x &\le& -24 \\ \color{#669900}{\div{-6}} && \color{#669900}{\div{-6}} &~~~~~|~ \text{Opposite Operations} \\ x &\color{#669900}{\ge}& 4 &~~~~~|~ \text{Flip the sign} \le~ \rightarrow ~\ge \text{because we divide by a negative number} \end{array}$