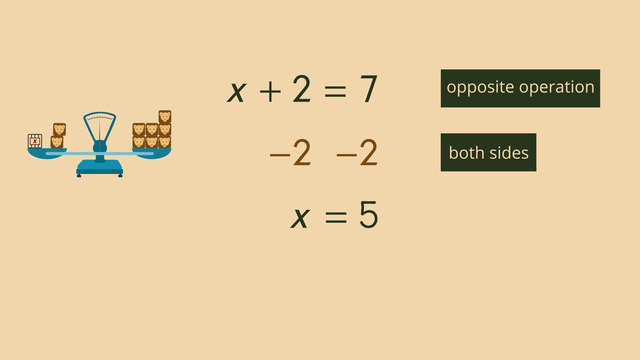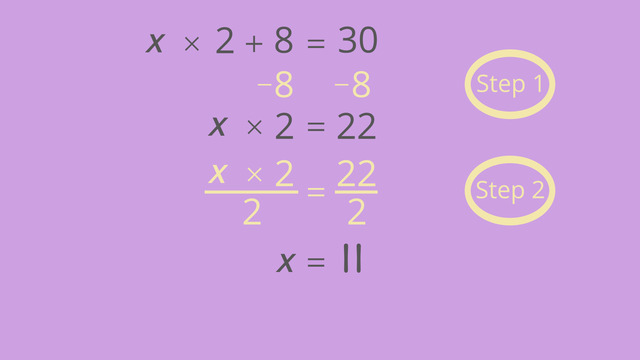Solving Multi-Step Equations with Variables on One Side

Solving Multi-Step Equations with Variables on One Side exercise

• Determine the best answer for each blank.

  Hints

  Remember that Sam rides the roller coaster one time fewer than Kayla.

  You can write all the money Kayla and Sam want to spend on the one side of the equation and the money they have to spend on the other side.

  One roller coaster ride costs $\$8$, so four rides cost $\$8\times 4=\$32$.

  Solution

  We want to know how many times Kayla and Sam can each ride the roller coaster. To figure this out, we assign the variable $x$ to the number of times Kayla can ride the roller coaster. Because Sam rides the roller coaster one time fewer than Kayla, he rides the roller coaster $x-1$ times.

  We can write the expression: $8\times x+8\times (x-1)$

  Pay attention to the parentheses. They are very important.

  Both Kayla and Sam ride the Ferris wheel just once. This gives us the expression $5+5$.

  Last but not least, Sam buys some cotton candy for $\$2$.

  We must add all of these expenses: $8\times x+8\times (x-1)+5+5+2$.

  Because they have $\$100$ to spend, the expression is set to equal $\$100$. This gives us the following equation:

  $\$8\times x+\$8\times (x-1)+\$5+\$5+\$2=\$100$

• Solve the equation.

  Hints

  You solve these equations by simplifying using the Distributive Property then Combining Like Terms and finally Isolating the Variable.

  To Isolate the Variable, we use Opposite Operations:

  • $+~\longleftrightarrow~-$
  • $\times~\longleftrightarrow~\div$

  Use Opposite Operations:

  • Multiplication ($\times~\longleftrightarrow~\div$)
  • Division ($\div~\longleftrightarrow~\times$)
  • Addition ($+~\longleftrightarrow~-$)
  • Subtraction ($-~\longleftrightarrow~+$)

  Solution

  Our equation is $8\times x+8\times (x-1)+5+5+2=100$.

  First, we use the Distributive Property to simplify $8\times(x-1)$ to $8x-8$:

  $8x+8x-8+5+5+2=100$

  Next, we Combine Like Terms on the left side of the equation:

  $16x+4=100$

  Now we can solve the equation by using Opposite Operations:

  $\begin{array}{rcrcl} 16x+4&=&100\\ \color{#669900}{-4}&&\color{#669900}{-4}&&| (\div~\leftrightarrow~\times) \text{ Opposite Operations}\\ 16x&=&96\\ \color{#669900}{\div16}&=&\color{#669900}{\div16}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&6 \end{array}$

  What does this solution mean?

  • Carla rides the roller coaster $6$ times
  • Sam can only ride $5$ times because he bought cotton candy instead.

• Evaluate how many times Kayla and Sam can ride the roller coaster.

  Hints

  • Organize the given information first.
  • Identify your variable.
  • Set up your equation.

  Use the opposite operations:

  • Multiplication ($\times~\longleftrightarrow~\div$)
  • Division ($\div~\longleftrightarrow~\times$)
  • Addition ($+~\longleftrightarrow~-$)
  • Subtraction ($-~\longleftrightarrow~+$)

  You can solve each equation by using the Distributive Property, Combining Like Terms and using Opposite Operations.

  Solution

  First, we have to set up the equation for each situation.

  $\mathbf{\$88}$ to spend:

  $8\times x+8\times(x-2)+5+5+5+5+2+2=88$.

  Now we solve the equation as follows:

  $\begin{array}{rcrcl} 8\times x+8\times(x-2)+5+5+5+5+2+2 &=&88&&|\text{ Distributive Property}\\ 8x+8x-16+5+5+5+5+2+2 &=&88&&|\text{ Combining Like Terms}\\ 16x+8 &=&88\\ \color{#669900}{-8}&&\color{#669900}{-8}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 16x &=&80\\ \color{#669900}{\div16}&&\color{#669900}{\div16}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&5 \end{array}$

  For $x=5$, this means that Carla rides the roller coaster five times while Sam rides it only three times.

  $\mathbf{\$119}$ to spend:

  $8\times (x-1)+8\times x+5+5+5=119$.

  Now we solve the equation as follows:

  $\begin{array}{rcrcl} 8\times (x-1)+8\times x+5+5+5&=&119&&|\text{ Distributive Property}\\ 8x-8+8x+5+5+5&=&119&&|\text{ Combining Like Terms}\\ 16x+7&=&119\\ \color{#669900}{-7}&&\color{#669900}{-7}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 16x&=&112\\ \color{#669900}{\div16}&&\color{#669900}{\div16}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&7 \end{array}$

  For $x=7$, this means that Sam rides the roller coaster seven times while Kayla rides it six times.

  $\mathbf{\$108}$ to spend:

  $8\times x+8\times x+5+5+5+5+2+2+2+2=108$.

  Now we solve the equation as follows:

  $\begin{array}{rcrcl} 8\times x+8\times x+5+5+5+5+2+2+2+2&=&108&&|\text{ Combining Like Terms}\\ 16x+28&=&108\\ \color{#669900}{-28}&&\color{#669900}{-28}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 16x&=&80\\ \color{#669900}{\div16}&&\color{#669900}{\div16}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&5 \end{array}$

  For $x=5$, this means that Kayla and Sam ride the roller coaster five times each.

  $\mathbf{\$98}$ to spend:

  $8\times x+8\times x+5+5+5+5+5+5+2+2=98$.

  Now we solve the equation as follows:

  $\begin{array}{rcrcl} 8\times x+8\times x+5+5+5+5+5+5+2+2&=&98&&|\text{ Combining Like Terms}\\ 16x+34&=&98\\ \color{#669900}{-34}&&\color{#669900}{-34}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 16x&=&64\\ \color{#669900}{\div16}&&\color{#669900}{\div16}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&4 \end{array}$

  For $x=4$, this means that Kayla and Sam both ride the roller coaster four times.

• Determine how many bags of candy Kayla and Sam can buy.

  Hints

  Use the Distributive Property:

  $a\times (b+c)=a\times b + a\times c$

  • The opposite operation of $+$ is $-$, and vice versa.
  • The opposite operation of $\times$ is $\div$, and vice versa.

  Solution

  Let's write a math equation to describe the situation:

  Teddy bears cost $\$2$ each Balloons cost $\$1$ each

  They buy two teddy bears one balloon, giving us:

  • $2+2+1$

  Kayla buys one bag fewer than Sam:

  • $1.50\times x+1.50\times(x-1)$

  Together they have $\$21.50$ to spend:

  $1.50\times x+1.50\times(x-1)+2+2+1=21.50$.

  We solve this equation as follows:

  $\begin{array}{rcrcl} 1.50\times x+1.50\times(x-1)+2+2+1&=&21.50&&|\text{ Distributive Property}\\ 1.50x+1.50x-1.50+2+2+1&=&21.50&&|\text{ Combining Like Terms}\\ 3x+3.5&=&21.5\\ \color{#669900}{-3.5}&&\color{#669900}{-3.5}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 3x&=&18\\ \color{#669900}{\div3}&&\color{#669900}{\div3}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&6 \end{array}$

  $x=6$ is the number of bags of candy Sam buys. Kayla buys one bag fewer. She buys $5$ bags. Together they buy $6+5=11$ bags of candy.

• Describe how to solve an equation.

  Hints

  Imagine an equation to be like a scale in balance:

  • You can move things on one or both sides of the scale but if you remove something from one side of the scale, you have to remove the same something on the other side as well.

  For example

  $\begin{array}{rcr} 6x+4&=&100\\ \color{#669900}{-4}&&\color{#669900}{-4}\\ 6x&=&96 \end{array}$

  is correct, but

  $\begin{array}{rcr} 6x+4&=&100\\ \color{#669900}{-4}&&\\ 6x&=&100 \end{array}$

  isn't.

  The opposite operations are:

  • $+~\longleftrightarrow~-$
  • $\times~\longleftrightarrow~\div$

  Solution

  An equation is like a scale in balance: We have terms on both sides of the equal sign.

  We can modify the equation by using the Distributive Property or by Combining Like Terms.

  Then to solve, we should Isolate the Variable by using Opposite Operations on both sides of the equation.

• Find and solve the equation for the given situation.

  Hints

  Example: If $x$ is the unknown value, two more would be $x+2$.

  The number of cats is the same in both examples.

  To isolate the variable $x$ we use opposite operations

  • $+~\longleftrightarrow~-$
  • $\times~\longleftrightarrow~\div$

  Solution

  Remember how to solve multi-step equations:

  1. Write the equation.
  2. Solve the equation.

  Cans of Food

  • Let the unknown number of cats be equal to $x$.
  • There are three more cats than dogs. $x-3$ is the number of dogs.
  • The total cans of food: $3\times x+2\times (x-3)$.
  • The pets consume 19 cans of food altogether:

  $3\times x+2\times (x-3)=19$.

  We use the Distributive Property then Combine Like Terms and finally Isolate the Variable as follows:

  $\begin{array}{rcrcl} 3\times x+2\times (x-3)&=&19&&|\text{ Distributive Property}\\ 3x+2x-6&=&19&&|\text{ Combine Like Terms}\\ 5x-6&=&19\\ \color{#669900}{+6}&&\color{#669900}{+6}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 5x&=&25\\ \color{#669900}{\div5}&&\color{#669900}{\div5}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&5 \end{array}$

  $x=5$ is the number of cats. Subtracting $3$ gives us the number of dogs, $2$.

  $\mathbf{\$3,400}$

  • Let the unknown number of cats be equal to $x$.
  • There is one more dog than there are cats: $x+1$ is the number of dogs.
  • The cost for the cats and the dogs is $200\times x+400\times (x+1)$.
  • Together Miss Crazycat and Miss Crazydog spent $\$3400$ on their pets:

  $200\times x+400\times (x+1)=3400$.

  Here we use the Distributive Property then we Combine Like Terms and finally we Isolate the Variable as follows:

  $\begin{array}{rcrcl} 200\times x+400\times (x+1)&=&3400&&|\text{ Distributive Property}\\ 200x+400x+400&=&3400&&|\text{ Combine Like Terms}\\ 600x+400&=&3400\\ \color{#669900}{-400}&&\color{#669900}{-400}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 600x&=&3000\\ \color{#669900}{\div600}&&\color{#669900}{\div600}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ x&=&5 \end{array}$

  $x=5$ is the number of cats. Adding $1$ gives us the number of dogs, $6$.