Relating Scale Drawings to Ratios and Rates


Basics on the topic Relating Scale Drawings to Ratios and Rates
After this lesson, you will be able to find the constant of proportionality and identify if a scale drawing is a reduction or enlargement of the original image.
The lesson begins by determining if an image is a true reduction. It leads you to organizing information in a table to find the constant of proportionality. It concludes with identifying the constant of proportionality for the enlargement of an image.
Learn about scale drawings by helping Malique reduce and enlarge his sketches!
This video includes key concepts, notation, and vocabulary such as the terms reduction (a scaled-down picture of the original image), enlargement (a scaled-up picture of the original image), scale drawing (a reduction or enlargement of an original image), how to represent the scale (a semi-colon between the length of the drawing and the length of the original), and that all lines, points, and figures must match between the scale drawing and original image.
Before watching this video, you should already be familiar with the phrase “constant of proportionality”, multiplying fractions, and identifying the larger or smaller of two values, particularly with fractions.
After watching this video, you will be prepared to learn about a scale factor, and to determine whether a given constant of proportionality makes the resulting scale drawing an enlargement or reduction.
Common Core Standard(s) in focus: 7.RP.A.2b A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Relating Scale Drawings to Ratios and Rates
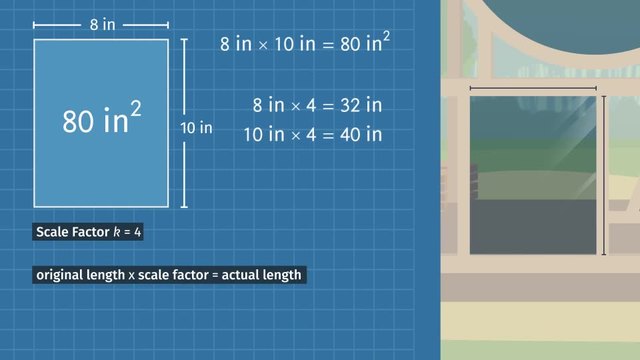
Malique is a young artist who is fascinated with the diversity of animal life, both past and present. He has come to the museum to make sketches of some interesting creatures. This woolly mammoth catches his eye, but fitting such a giant beast in his small sketchbook will be a challenge! Malique will need to create a scale drawing, then use his knowledge of ratios to make sure it’s accurate. Malique draws a sketch of the mammoth. Is his sketch larger or smaller than the actual mammoth? Smaller of course! His drawing needs to be smaller than the original to fit in the sketchbook. But is his drawing an accurate REDUCTION of the original? Because a reduction is a proportionally scaled-down image of the original, we’ll need to take some measurements, and see if the drawing is proportional to the original. If it is, then we can say it’s a SCALE drawing, and a true reduction! The original mammoth is gigantic! Its height is 250 centimeters. That's basically the height of two 8-year-olds. The mammoth's length is 400 centimeters. Almost the length of the average car. What a fantastic creature! Malique’s drawing has a height of 5 centimeters and a length of 8 centimeters. A mammoth can fit in his sketchbook after all! Let's organize the information using a table to see if it is a true scale drawing. First, we'll record the original height and length. Followed by the drawing height and length. This gives us our organized information all written in centimeters. An image is a scale drawing if its corresponding measurements are proportional to those of the original. In order to find out if they are proportional, we need to see if the ratios of corresponding measurements are equal. That means we should create ratios of height to height, and length to length and write the ratios of drawing to original. This will help us find the constant of proportionality. So, let’s substitute our known values for the heights into the ratios. That’s 5 to 250. And the ratio of the drawing length to the original length is 8 to 400. It’s hard to tell if they’re the same, so let’s reduce each ratio. 5 over 250 reduces to 1 over 50. 8 over 400 reduces to 1 over 50 as well! The ratios are equal, which means Malique has made an accurate scale drawing. 1 over 50 is the constant of proportionality 'k', which represents the relationship between the scale-drawing and the original. When the constant of proportionality is between 0 and 1, the image is a reduction of the original. Good job, Malique, on creating a scale drawing reduction. What are you drawing next? Bugs? Really, Malique? Well I guess these beetles are such intricate little creatures. How will Malique show the world their complexity? Do you think he’ll want to sketch a reduction or an enlargement? An enlargement would be best to highlight their features! An enlargement is a proportionally scaled-up image of the original. The original beetle is 6 centimeters long by 2 centimeters wide. And Malique’s drawing is 12 centimeters long by 6 centimeters wide. Let's organize this information using a table. Similar to before, we'll record the original length and width. Followed by the drawing length and width. Again this gives us our organized information all written in centimeters, so that we can easily identify the ratios. If the ratios of corresponding measurements are the same, the drawing will be a true enlargement. Remember, we should first set-up ratios of corresponding measurements, such as length to length or width to width. And keep the ratio order of drawing to original. The ratio of the lengths is 12 to 6, and the ratios of widths is 6 to 2. We'll need to reduce the ratios to see if they are equal. 12 over 6 reduces to 2 and 6 over 2 reduces to 3? Those are NOT the same! The ratios are not proportional. In fact, if you look closely at the drawing, you can see that it’s a bit distorted. Malique's drawing is too wide! To draw a true enlargement, the drawing width should be 4 cm. So, instead of a drawing width of 6 centimeters from our earlier calculations let’s correct it to be 4. That means the ratio of the widths simplifies to be two as well. Two is our constant of proportionality. Since the ratios are equal they are proportional! Therefore, we now have a true scale drawing. It is an enlargement because the constant of proportionality, 'k', is greater than 1. Let’s review what we've learned. To determine if we’ve got a scale drawing, set-up two ratios of corresponding measurements. Use the ratio drawing to original to calculate the constant of proportionality. If the ratios are the same then the drawing and original are proportional. This proportionality means we DO have a scale drawing. It's a reduction if the constant of proportionality is between 0 and 1. And it's an enlargement if the constant of proportionality is greater than than one. Great sketches, Malique. You really—WAIT. What is THAT? Maybe, uh, just an enlargement of one of the exhibits? Ah c’mon, man. That's not cool!