Ratios


Basics on the topic Ratios
After this lesson, you will be able to describe a ratio of two quantities.
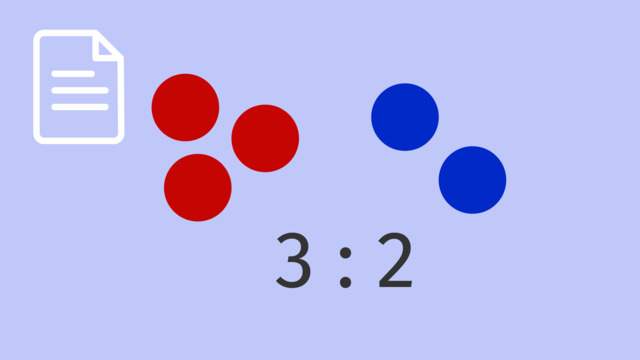
The lesson begins by teaching you that a ratio describes a relationship between two quantities. It leads you to learn that ratios can be written in a variety of ways, such as 3:2, 3/2, or “3 to 2”. It concludes with a reminder that with ratios, order matters!
Learn about ratios by helping Leelee make her food blog go viral!
This video includes key concepts, notation, and vocabulary such as ratio (a relationship between two non-negative numbers, both of which are not zero); a tape diagram (a visual representation of a ratio); and how to read ratio notation (3:2 is read “3 to 2”).
Before watching this video, you should already be familiar with multiples, fractions, and terms such as “for each” and “for every”.
After watching this video, you will be prepared to learn how to determine equivalent ratios using tape diagrams and ratio tables, how to use complex ratios that can be reduced; and how to apply ratios to rate or slope.
Common Core Standard(s) in focus: 6.RP.A.1 A video intended for math students in the 6th grade Recommended for students who are 11 - 12 years old
Transcript Ratios
In her latest attempt to get internet famous, Leelee has decided to start her own online Food Vlog Channel... the FOOD QUEEN EXTREME!
Leelee isn't exactly an expert chef, but who needs cooking skills when you've got the recipe for using perfect ratios!
Let's take a look at what Leelee is making first: Major League Cheesy Potatos.
The recipe calls for 3 parts potato for every 1 part cheese.
The relationship between the amount of potatoes in her recipe and the amount of cheese is called a ratio.
We can write it using the word 'to' like this, or using a colon like this, or as a fraction like this.
No matter how we write it, each of these ratios is read as "3 to 1."
The meaning of the numbers, and their order, is given to Leelee in the recipe. Potatoes first, followed by the cheese.
But if Leelee makes a mistake, and flips the ratio. Now the ratio is one part potato for every three parts cheese!
A potato to cheese ratio of 1 to 3 would be crazy cheesy!
This is why with ratios, order matters.
It's just like with fractions: three over one is not the same as one-third.
Ok, that was a great recipe for people who love cheesy ballpark food, but up next is something on the lighter side.
Yoga-Berry Banana Smoothies!
The recipe calls for 4 parts strawberry for every 3 parts banana.
But this recipe only works for one person. How does Leelee blend for more than one?
We've already seen a few ways to write ratios. Now let's see how we can use a table to organize our information.
We know that for every 4 parts strawberry, we need 3 parts banana.
How about smoothies for two? If we double the parts of strawberry, we’ll have 8 parts strawberry, and we’ll need 6 parts of banana.
And for three people?
That’s a ratio of 12 parts strawberries to 9 parts bananas.
We know the perfect 4 to 3 ratio is still in the smoothie, because if we write the ratios as fractions, the fractions are equal.
12 over 9 reduces to 4 over 3.
Can Leelee make an extreme smoothie for a yoga class of 10 people?
I think we're gonna need a bigger blender!
The last recipe on Leelee's list is for Chew-Mocha Brownies.
It features three parts caramel for every five parts chocolate.
We can represent this relationship in yet another way: a tape diagram.
In this diagram, each of the small rectangles represents one part of the whole.
This shows the ratio of caramel to chocolate as 3 to 5.
But how can we use the diagram to help us double Leelee's recipe?
Simply by changing the value of each rectangle from 1 to 2, the top 3 rectangles now represent 6 parts caramel, and the 5 rectangles on the bottom represent 10 parts chocolate.
Now we have the equivalent ratio, 6 to 10.
If we look at the ratios as fractions, six-tenths reduces to three-fifths, so we know that they are equal.
To review...
Ratios describe a relationship between two numbers.
They can be represented with the word 'to' or with a colon in standard ratio notation or as fractions.
They can also be visually represented with tables and tape diagrams.
And remember: with ratios order matters!
Looks like Leelee is all ready to give her brownies a taste-test.
Hey Leelee! Give a shout-out to all your fans, how did they turn out?
Ratios exercise
-
Determine the ratio that corresponds to each tape diagram.
HintsRatios can be represented in three different ways and can be simplified:
- $4$ to $6$ equals $2$ to $3$
- $4:6$ equals $2:3$
- $\frac{4}{6}=\frac{2}{3}$
The ratio $1:3$ matches the tape diagram in the image.
The ratio $8$ to $4$ equals $2$ to $1$, and matches the tape diagram in the image.
SolutionRatios can be written in three different ways: $1$ to $3$; $1:3$; and $\frac{1}{3}$. They can also be visually represented with tables and tape diagrams.
Remember that with ratios, order matters! $1:3$ is very different from $3:1$.
1. The ratio $4$ to $5$ matches the tape diagram with $4$ blocks on top and $5$ blocks on the bottom.
2. The ratio $\frac{3}{4}$ matches the tape diagram with $3$ blocks on top and $4$ blocks on the bottom.
3. The ratio $3:6$ simplifies to $1:2$, and matches the tape diagram with $1$ block on top and $2$ blocks on the bottom.
4. The ratio $5$ to $3$ matches the tape diagram with $5$ blocks on top and $3$ blocks on the bottom.
5. The ratio $\frac{6}{4}$ simplifies to $\frac{3}{2}$, and matches the tape diagram with $3$ blocks on top and $2$ blocks on the bottom.
6. The ratio $5:2$ matches the tape diagram with $5$ blocks on top and $2$ blocks on the bottom.
-
Identify which ratios correspond to each table.
HintsRatios can be represented in three different ways and can be simplified:
- $4$ to $6$ equals $2$ to $3$
- $4:6$ equals $2:3$
- $\frac{4}{6}=\frac{2}{3}$
Remember that with ratios, order matters! The ratio of $2$ to $3$ is very different from $3$ to $2$.
In the table, the ratios $9:12$ and $6:8$ both represent the smallest ratio $3:4$ for the reasons represented below:
- If you divide both sides of the ratio $9:12$ by the GCF $3$, it simplifies to $3:4$.
- If you if you divide both sides of the ratio $6:8$ by the GCF $2$, it also simplifies to $3:4$.
SolutionTable 1
All ratios that simplify to $2$ to $5$.
- The GCF for $6$ and $15$ is $3$. Divide both parts of the ratio $6:15$ by $3$, then $6:15$ equals $2:5$.
- The GCF for $8$ and $20$ is $4$. Divide both parts of the ratio $8$ to $20$ by $4$, then $8$ to $20$ equals $2$ to $5$.
- The ratio $2:5$ is another way to write $2$ to $5$.
- The GCF for $10$ and $25$ is $5$. Divide both parts of the ratio by $5$ then $\frac{10}{25}=\frac{2}{5}$.
All ratios that simplify to $1$ to $2$.
- The GCF for $4$ and $8$ is $4$. Divide both parts of the ratio $4$ to $8$ by $4$, then $4$ to $8$ equals $1$ to $2$.
- The GCF for $2$ and $4$ is $2$. Divide both parts of the ratio $2:4$ by $2$, then $2:4$ equals $1:2$.
- The GCF for $10$ and $20$ is $10$. Divide both parts of the ratio $\frac{10}{20}$ by $10$, then $\frac{10}{20}=\frac{1}{2}$.
- The GCF for $9$ and $18$ is $9$. Divide both parts of the ratio $9:18$ by $9$, then $9:18$ equals $1:2$.
All ratios that simplify to $3$ to $2$.
- The GCF for $9$ and $6$ is $3$. Divide both parts of the ratio $\frac{9}{6}$ by $3$, then $\frac{9}{6}=\frac{3}{2}$.
- The GCF for $12$ and $18$ is $4$. Divide both parts of the ratio $12$ to $8$ by $4$, then $12$ to $8$ equals $3$ to $2$.
- The ratio $\frac{3}{2}$ is another way to write $3$ to $2$.
- The GCF for $15$ and $10$ is $5$. Divide both parts of the ratio $15:10$ by $5$, then $15:10$ equals $3:2$.
-
Complete the table for each ratio.
HintsIn a ratio, order matters. This means that the ratio $4:5$ is not the same as the ratio $5:4$.
To find an equivalent ratio, multiply both parts of the original ratio by the number of servings. For example, if 1 serving is the ratio $1:2$, then 3 servings would be the ratio $3:6$.
Ginger Berry Smoothie
- $1$ serving is $1$ ginger to $3$ strawberries
- $2$ servings: $2$ to $6$
- $4$ servings: $4:12$
SolutionTo complete the tables, find the ratios by multiplying the original ratio by the number of servings.
It is important to remember that in a ratio, order matters. This means that the ratio $4:5$ is not the same as the ratio $5:4$.
1. Berry Blast Smoothie
- $1$ serving is $5$ raspberries to $3$ blueberries
- $2$ servings (Multiply both numbers by $2$): $10$ to $6$
- $5$ servings (Multiply both numbers by $5$): $25:15$
- $1$ serving is $2$ pineapples to $4$ mangos
- $3$ servings (Multiply both numbers by $3$): $6$ to $12$
- $7$ servings (Multiply both numbers by $7$): $14:28$
- $1$ serving is $6$ kale to $4$ spinach
- $4$ servings (Multiply both numbers by $4$): $24$ to $16$
- $5$ servings (Multiply both numbers by $5$): $30:20$
-
Create the tape diagram for each ratio.
HintsBoth sides of the ratio $25:100$ can be divided by their greatest common factor, $25$, and simplify to, $1:4$.
The top row of the tape diagram represents the left side of the ratio (or numerator), and the bottom row of the tape diagram represents the right side of the ratio (or denominator).
The tape diagram represents the ratio of $\frac{25}{75}$.
Solution1. If you divide both sides of the ratio, $11$ to $44$, by the GCF, $11$, the simplified ratio is $1$ to $4$. The tape diagram shows $1$ yellow square on top and $4$ yellow squares on the bottom.
2. If you divide both sides of the ratio, $14:21$, by the GCF, $7$, the simplified ratio is $2:3$. The tape diagram shows $2$ yellow squares on top and $3$ yellow squares on the bottom.
3. If you divide both sides of the ratio, $\frac{60}{20}$, by the GCF, $20$, the simplified ratio is $\frac{3}{1}$. The tape diagram shows $3$ yellow squares on top and $1$ yellow square on the bottom.
-
Select the true statements about ratios.
HintsRatios can be represented in three different ways:
- $1$ to $3$
- $1:3$
- $\frac{1}{3}$
The ratio $2:4$ is equivalent to the ratio $1:2$ because $\frac{2}{4}=\frac{1}{2}$.
The ratio $3$ to $1$ is very different from the ratio $1$ to $3$.
SolutionTrue Statements
- The ratio $\frac{1}{3}$ can be represented as $1:3$.
- A ratio is a relationship between two amounts.
- The ratio, $\frac{8}{18}=\frac{4}{9}$.
- Tape diagrams visually represent ratios.
- $3$ cups of sugar for every $2$ cups of flour is equivalent to $6$ cups of sugar for every $4$ cups of flour.
- In a ratio, order matters.
The ratio, $12:9$, is equal to $3:4$.
- This statement is false because dividing the ratio $12:9$ by $3$ results in a ratio of $4:3$. Another way to view the ratio is to set it up as a fraction, $\frac{12}{9}=\frac{4}{3}$. Remember, in a ratio order matters!
- The statement is false because the ratio $4:8$ represented as a fraction is $\frac{4}{8}=\frac{1}{2}$, not $\frac{2}{1}$. Remember, in a ratio order matters!
- The ratio $3:4$ can be represented as $3$ to $4$ or $\frac{3}{4}$, not $3 \times 4$.
-
Determine which table goes with which tape diagram.
HintsSet up one row of numbers as a fraction, and reduce:
- $\frac{12}{20}=\frac{3}{5}$
The tape diagram represents the ratio $3:5$.
Remember that with ratios, order matters!
Solution- The ratio of peanuts to almonds is $1:3$. You can find this by simplifying any of the pairs of numbers in the table. The first line is $\frac{3}{9}=\frac{1}{3}$. Therefore, the tape diagram has $1$ block on top and $3$ blocks on the bottom.
- The ratio of green to red is $4:7$. You can find this by simplifying any of the pairs of numbers in the table. The first line is $\frac{8}{14}=\frac{4}{7}$. Therefore, the tape diagram has $4$ blocks on top and $7$ blocks on the bottom.
- The ratio of oranges to apples is $5:3$. You can find this by simplifying any of the pairs of numbers in the table. The first line is $\frac{10}{6}=\frac{5}{3}$. Therefore, the tape diagram has $5$ blocks on top and $3$ blocks on the bottom.
- The ratio of girls to boys is $3:4$. You can find this by simplifying any of the pairs of numbers in the table. The first line is $\frac{6}{8}=\frac{3}{4}$. Therefore, the tape diagram has $3$ blocks on top and $4$ blocks on the bottom.
- The ratio of tomatoes to carrots is $1:2$ or any multiple of the ratio $1:2$. Therefore, the tape diagram has $5$ blocks on top and $10$ blocks on the bottom.


















LOOOOLLLL
Very helpful