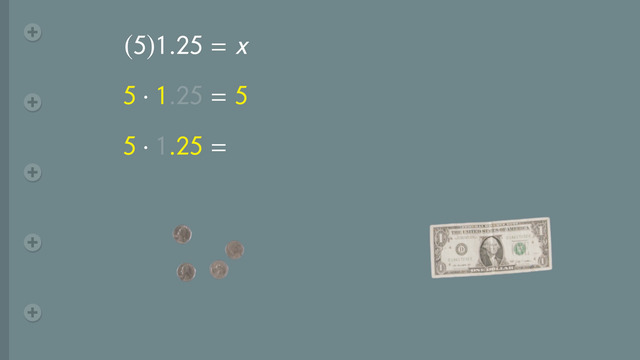One-Step Equations with Multiplication and Division


Basics on the topic One-Step Equations with Multiplication and Division
After this lesson, you will be able to solve real-world mathematical problems using one-step equations with multiplication or division.
The lesson begins by teaching you how to identify given quantities and pinpoint the missing value. It leads you to learn how to set-up the one-step equation needed to find the missing value. It concludes with showing you how to identify which operation to use to solve the equation.
Learn about one-step equations by finding out how Henry planned his nature trip.
This video introduces new concepts, notation, and vocabulary such as the phrase “isolating the variable”, which is a way of solving an equation by using opposite operations to position the variable by itself on one side of the equation.
Before watching this video, you should already be familiar with variables, coefficients, and opposite operations, specifically multiplication and division.
After watching this video, you will be prepared to represent more complex real-world situations using equations and solve them using multi-step operations.
Common Core Standard(s) in focus: 6.EE.B.7 A video intended for math students in the 6th grade Recommended for students who are 11 - 12 years old
Transcript One-Step Equations with Multiplication and Division
Henry David lives in New York, and he is very annoyed by how crowded and loud the city is. Therefore, he has decided to go on a backpacking trip to Alaska. He has a guidebook and knows just the place to go this is exactly what he was looking for! Just pure, unadulturated peace and quiet. To plan his trip, he uses One Step Equations with Multiplication and Division. Henry David is extremely thorough in his preparations and wants to make sure he takes sufficient provisions for his journey. He needs to calculate how many days his provisions will last. Henry knows that he'll need 6 lbs. of food each day, and he can carry 30 lbs of food in his backpack. So, how many days will his provisions last? To figure this out, we first have to set up an equation. As you know, an equation is like a scale that is balanced. Both sides of an equal sign have the same value. Since we want to calculate the number of days Henry's provisions will last, let the number of days be represented by 'd'. Mathematically, 6 times 'd', or 6d, represents the amount of food, in pounds, consumed after 'd' days. Because Henry can carry 30 lbs. of food in his backpack, the number of days, 'd', times 6 lbs consumed each day equals 30 lbs. Let’s see how many days Henry's provisions will last. As you've probably guessed, One Step Equations can be solved in only one step. You just have to use the correct operation. We want to isolate the variable 'd', which is multiplied by 6 on the left side of the equation. If you see a variable multiplied by a coefficient, you can isolate the variable by dividing; in this case, by 6. But remember, since equations are like scales that need to be balanced, you have to divide by 6 on both sides of the equation. 6d divided by 6 is just 'd', so we've isolated our variable and 30 divided by 6 is 5. Henry David's got 5 days' worth of provisions. Now let's see if he can make it to his destination on foot with those provisions. How many total miles can Henry walk during his 5 days if we know his average speed is 12 miles per day? Translating our word problem into mathematics we can setup this equation.
We can use the variable 'm' for our unknown total miles. And since we already know the total number of days and his average speed we can go ahead and substitute 5 for total days and 12 for miles per day. Again, we need to isolate our variable. The variable 'm' is divided by 5. What's the opposite of division? If you said multiplication, you're right! We should multiply BOTH sides by 5. You might also see the left side written like this: This makes it easier to see that the 5s cancel each other out. So we're left with 12 times 5, giving us 'm' equals 60. This means Henry can travel 60 miles in 5 days at a rate of 12 miles per day. With his destination just 60 miles away, Henry David advances confidently in the direction of his dreams. As long as he doesn't run into any complications, he should make it to his destination on time with enough provisions. He's finally made it to the great place described in the guidebook! That really doesn’t look like what he expected.
One-Step Equations with Multiplication and Division exercise
-
Recall how to solve one-step equations.
HintsHenry knows that he needs $6$ pounds of food per day and that he can carry $36$ pounds. How many days will Henry have food?
Let $d$ represents the number of days, the equation is then $6d=36$.
If Henry walks at an average speed of $12$ miles per day, for $3$ days, how many total miles can Henry walk?
Let $m$ be the total number of miles. The equation is then $\frac{m}{3}=12$.
To solve $6d=36$, divide both sides of the equation by $6$. We then have that $d=6$.
To solve $\frac{m}{3}=12$, multiply both sides of the equation by 3. We then have that $m=36$.
SolutionHenry wants to calculate how many days his food will last him. He knows that he will need $5$ pounds of food per day and that he can carry $20$ pounds in his backpack. To figure this out, let's set up an equation.
- First, we need to identify the unknown. Since we don't know the number of days his food will last him, we will let the variable $d$ represent the number of days.
- Since Henry knows that he needs $5$ pounds per day, we can translate this phrase into the expression $5d$. We are told he can carry a total of $20$ pounds in his backpack. Therefore, the equation is, $5d=20$.
- To solve for the unknown we will need to isolate $d$.
- Since $d$ is being multiplied by $5$, we need to use opposite operations and divide by $5$ on both sides to keep the equation balanced.
- Doing so, we have $5d\div 5=20\div 5$.
- The $5$'s cancel out on the left side of the equation. We then find that $d=4$.
Now Henry needs help figuring out how many miles he can walk in $4$ days if his average speed is $11$ miles per day.
This problem can be represented as the math equation, $\frac{\text{miles}}{\text{days}}=\text{miles per day}$.
- First, we need to identify the unknown. Since we don't know the number of miles Henry can walk in $4$ days, we will let the variable $m$ represent the total number of miles.
- Now we can fill in the equation, $\frac{\text{miles}}{\text{days}}=\text{miles per day}$, by substituting $m$ for miles, $4$ for days, and $11$ for miles per day. The equation we get is then $\frac{m}{4}=11$.
- To solve for the unknown we will need to isolate $m$.
- Since $m$ is being divided by $4$, we will use opposite operations and multiply by $4$ on both sides to keep the equation balanced.
- Doing so, we have $\frac{m}{4}\cdot 4=11\cdot 4$.
- The $4$'s cancel out on the left side of the equation. Therefore, $m=44$.
-
Identify which operation needs to be used to isolate the variable.
HintsTo isolate a variable, use the opposite operation.
For example, if a number is being added to the variable $m$, then use subtraction get isolate $m$.
$x+2=3$
- Since $2$ is being added to $x$, use subtraction to isolate $x$.
- Since $2$ is being subtracted from $x$, use addition to isolate $x$.
$2x=3$
- Since $x$ is being multiplied by $2$, use division to isolate $x$.
- Since $x$ is being divided by $2$, use multiplication to isolate $x$.
SolutionUse the opposite operations to isolate the variable in the equation.
This is also known as the additive inverse for addition and subtraction problems, and the multiplicative inverse for multiplication and division problems.
$y-32=6$
- Since $32$ is being subtracted from $y$, use addition to isolate $y$.
- Since $74$ is being subtracted from $p$, use addition to isolate $p$.
- Since $5$ is being added to $r$, use subtraction to isolate $r$.
- Since $1$ is being added to $m$, use subtraction to isolate $m$.
- Since $c$ is being divided by $4$, use multiplication to isolate $c$.
- Since $m$ is being divided by $5$, use multiplication to isolate $m$.
- Since $d$ is being multiplied by $6$, use division to isolate $d$.
- Since $x$ is being multiplied by $4$, use division to isolate $x$.
-
Write and solve one-step equations.
HintsSolve each equation by thinking about which opposite operation must be applied to the equation to get the variable by itself.
In the equation $5x=35$, since $x$ is being multiplied by $5$, the opposite operation is to divide both sides by $5$ so that $x=7$.
In the equation $x-6=12$, since $6$ is being subtracted from $x$, the opposite operation is to add $6$ to both sides so that $x=18$.
SolutionThe number of days Henry's water supply will last if he needs $3$ bottles per day and he can carry $24$ in his backpack.
- Let $x$ be the number of days.
- The equation is $3x=24$.
- The opposite operation is to divide both sides by $3$.
- $x=8$
- Let $x$ be the number of miles.
- The equation is $x+48=60$.
- The opposite operation is to subtract $48$ from both sides.
- $x=12$
- Let $x$ be the number of hot dogs.
- The equation is $x-5=30$.
- The opposite operation is to add $5$ to both sides.
- $x=35$
- Let $x$ be the number of hours.
- The equation is $\frac{x}{6}=7$.
- The opposite operation is to multiply each side by $6$.
- $x=42$
-
Calculate the solution for each one-step equation.
Hints- $ m+6$ is the same as $6+m$ because of the commutative property of addition.
- $m6$ is the same as $6m$ because of the commutative property of multiplication.
To solve a one-step equation, use the opposite operation to isolate the variable.
$m+6=12$
- Opposite operation is to subtract $6$.
- Opposite operation is to add $6$.
- Opposite operation is to divide $6$.
- Opposite operation is to multiply $6$.
Solution1. $4m=-12$
- The opposite operation is to divide by $4$ on both sides.
- $\frac{4m}{4}=\frac{-12}{4}$
- $m=-3$
- The equation can also be written as $m+6=12$ because of the commutative property of addition.
- The opposite operation is to subtract $6$ from both sides.
- $m+6-6=12-6$
- $m=6$
- The opposite operation is to multiply $-2$ on both sides.
- $\frac{m}{-2}\cdot -2=4\cdot -2$
- The opposite operation is to add $9$ to both sides.
- $m-9+9=2+9$
- $m=11$
- The equation can also be written as $7\cdot m=14$ because of the commutative property of multiplication.
- The opposite operation is to divide by $7$ on both sides.
- $\frac{7\cdot m}{7}=\frac{14}{7}$
- $m=2$
- The opposite operation is to subtract $10$ from both sides.
- $m+10-10=15-10$
- $m=5$
-
Determine which statements are true about one-step equations.
Hints$k+3=15$
- Since $1$ is being added to $k$, we need to use the opposite operation and subtract $1$ from both sides of the equation to isolate the variable $k$.
- Using the opposite operation is the same as using the additive inverse.
$3k=15$
- Since $k$ is being multiplied by $3$, we need to multiply by the multiplicative inverse of $3$, which is $\frac {1}{3}$, to isolate the variable $k$.
- Using the multiplicative inverse is the same as using the opposite operation.
$\frac{k}{3}=15$
- Since $k$ is being divided by $3$, we need to multiply both sides by $3$ to isolate the variable $k$.
SolutionTrue Statements
- For the equation $d+7=10$, to isolate the variable $d$ we must add the additive inverse of $7$, which is $-7$, to both sides of the equation.
- For the equation $4d=16$, since $d$ is being multiplied by 4, we must use the opposite operation and divide both sides of the equation by $4$ to isolate the variable $d$.
- For the equation $\frac{x}{2}=24$, to isolate the variable $x$ we must multiply both sides of the equation by the multiplicative inverse of $\frac{1}{2}$, which is $2$.
- For the equation $c-8=9$, since $8$ is being subtracted from $c$, we must use the opposite operation and add $8$ to both sides of the equation in order to isolate the variable $c$.
False Statements
For the equation $m+2=15$, to isolate the variable $m$, we must add the additive inverse of $15$, which is $-15$, to both sides of the equation.
- The correct statement is: For the equation $m+2=15$, to isolate the variable $m$, we must add the additive inverse of $2$, which is $-2$, to both sides of the equation.
- The correct statement is: For the equation $3y=21$, to isolate the variable $y$ we must multiply by the multiplicative inverse of $3$, which is $\frac{1}{3}$, to both sides of the equation.
-
Solve the one-step and two-step equations.
HintsTo solve one-step and two-step equations, think of the opposite operations that are needed to isolate the variable.
One-Step Equations:
- If $-2m=8$, divide both sides by $-2$ so that $m=-4$.
- If $\frac{m}{-2}=8$, multiply both sides by $-2$ so that $m=-16$.
- If $m-2=8$, add $2$ to both sides so that $m=10$.
- If $m+2=8$, subtract $2$ from both sides so that $m=6$.
Two-step equations are very similar to one-step equations. The only difference is that you have to think about two opposite operations to get the variable alone.
- $2m-5=11$
- The first opposite operation is to add $5$ to both sides, so that $2m=16$.
- The second opposite operation is to divide both sides by $2$ to get $m=16$.
SolutionOne-Step Equations:
1. $-2m=24$
- The opposite operation is to divide both sides by $-2$ so that $m=-12$.
- The opposite operation is to multiply both sides by $4$ so that $m=28$.
- Two-step equations are very similar to one-step equations. The only difference is that you have to think about the two opposite operations to get the variable alone.
- The first opposite operation is to subtract $5$ from both sides to get $2m=14$
- The second opposite operation is to divide both sides by $2$ to get $m=7$.
- The first opposite operation is to add $3$ to both sides to get $5m=10$.
- The second opposite operation is to divide both sides by $5$ to get $m=2$.
- The first opposite operation is to add $5$ to both sides to get $2m=8$.
- The second opposite operation is to divide both sides by $2$ to get $m=4$.