Linear and Nonlinear Expressions

Basics on the topic Linear and Nonlinear Expressions
Linear and nonlinear equations play a prominent role in many disciplines such as engineering, physics, arts, economics, and biology. Directly proportional relationships in real life, like that between voltage and current, or that between mass and weight of an object, are considered linear. On the other hand, real-world applications of nonlinear equations include triangulation of GPS signals, conservation of mechanical energy when there is an elastic collision, manufacture of electronic parts, and design of the architecture of buildings. Learn about linear and nonlinear equations by helping the city attorney prove to the judge in a traffic court that Mofa, a scooter-rider enthusiast, has been driving recklessly off road by presenting the graphs of linear and nonlinear equations as evidences. Common Core Reference: CCSS.MATH.CONTENT.8.FA.3
Transcript Linear and Nonlinear Expressions
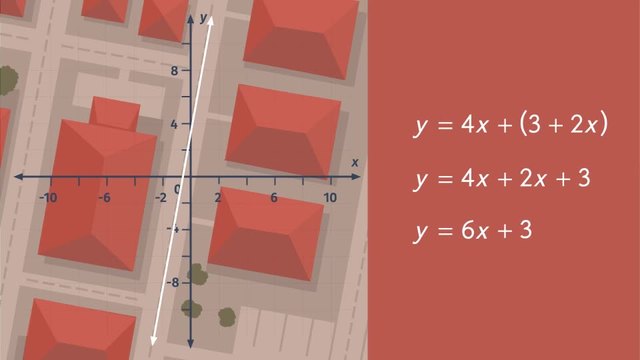
While riding his scooter, Mofa loves to put the pedal to the metal and tear up the back roads. But he's amassed a pile of tickets for driving recklessly and now, he's in a heap of trouble. Today, he's in traffic court trying to fight the charges. He tells the judge that he did nothing wrong all he did was drive in a perfectly straight line, following the perfectly straight roads. But, the city attorney isn’t having any of it. He knows that Mofa drove off road and he's going to prove it using the graphs of linear and nonlinear equations. All the streets in Linear City are perfectly straight and can be represented by linear equations. Linear equations contain variables raised to the first power. That means an equation is not considered to be linear if, when written in its simplest form, any of the variables are in a denominator under a radical...squared...cubed...or raised to a higher power. When graphed, a linear equation is a straight line. Let’s take a look at an example of a route Mofa drove. y' is equal to 4x plus the quantity '3 plus 2x'. Let's simplify this equation. First, reorder the terms to put the like terms together. Then, combine like terms giving us the simplified equation, 'y' is equal to 6x plus 3. Since the exponent of each variable is equal to one the equation is a first degree equation. Remember, when an exponent is equal to one, the exponent is most often assumed, not written. But what about equations that have variables raised to powers other than one? These equations are called nonlinear equations! Nonlinear equations also include rational expressions where a variable is in the denominator when written in simplest form. Nonlinear is just another way of saying the graph of an equation is not a straight line. Let’s take a look at an example of a nonlinear equation. Here's 'y' equals 2 over 'x'. This is a rational equation, meaning at least one term is expressed as a fraction. Look at those curves! Because the graph of this equation is not a straight line, it is a nonlinear equation and therefore, not a road in Linear City. Let's take a look at another route Mofa took that he claims was in a straight line. Mofa's route can be represented by the equation 'y' is equal to 'x' plus the sum of 'x' and one plus the difference of 'x' and two. To rewrite the equation, first group like terms and then simplify. We get the equation 'y' is equal to 3x minus 1. Is this equation linear or nonlinear? Since the variables are raised to the first power, this is a linear equation. But let's check the surveillance footage. Sure enough, Mofa was driving in a straight line! But wait! There's more evidence to be presented. This equation doesn't look linear, because the variable 'x' is cubed. But let's investigate by graphing. First, use the distributive property to get rid of the parentheses. Then, reorder the terms according to standard form to get 'y' equals -4x to the third plus 8. Now we can graph. Whoa! Mofa was driving WAY out of control! That is definitely not a straight line and not a linear equation. Mofa’s in big trouble because there’s still more evidence against him. This is when Mofa drove the route 'y' equals 'x' squared here's when he drove the route 'y' equals the square root of x and, here's 'xy' equals 5 which, after isolating the 'y' gives us 'y' is equal to 5 divided by 'x'. Oh man, none of these routes are straight lines and none of these equations are linear. With plenty of evidence against him, the judge is ready to rule. Mofa is definitely going to have to pay a fine or maybe worse! Oh no, it looks like they confiscated his sweet ride but I guess one wheel is better than none!
Linear and Nonlinear Expressions exercise
-
Identify if an equation is linear and nonlinear.
HintsLinear equations contain variables raised to a power of $1$.
Each equation which is not linear is nonlinear.
$y=x^2+1$ is an example of a nonlinear equation.
Keep in mind: instead of writing $x^1$, we usually just write $x$.
SolutionLinear equations contain variables raised to a power of $1$.
In other words: An equation is not linear and thus nonlinear if the variable is in the denominator, or squared, or cubed, or raised to another power greater than $1$. Another example for a nonlinear equation is given by $y$ equals the square root of $x$.
So, now we are in the position to detect all linear equations. Those are:
- $y=6x+3$
- $y=3x-1$
All other equations are nonlinear:
- $y=\frac2x$ as well as $y=\frac5x$ are rational equations.
- $y=x^2$ is a square equation.
- $y=-4x^3+8$ is a cube equation.
- $y=\sqrt x$ is a root equation.
-
Identify which graphs are linear and which are nonlinear.
HintsThe graph of a linear equation is a straight line.
All variables in a linear equation are raised to the power of $1$.
Just two graphs show linear equations.
SolutionHow can you decide if an equation is linear or nonlinear just by looking at its graph?
The graph of a linear equation is always a straight line.
If the graph is not a straight line, its corresponding equation must be nonlinear.
The following are linear equations:
- $y=6x+3$
- $y=3x-1$
-
Find the nonlinear terms in the equations.
HintsFirst, look at the exponents of the variables: if any exponent is greater than $1$, the equation can't be linear.
An equation with any variable under a radical or in a denominator is nonlinear.
Mofa found three possible routes that are linear.
SolutionMofa wants to avoid further traffic tickets, so he plans his routes and writes down some equations. Unfortunately there are still some nonlinear equations. Those routes will lead to big trouble, so he has to exclude them.
Keep in mind: All variables in linear equations are raised to the power of $1$, which is usually not written down.
- $y+x=5$ Sure, this is a linear equation.
- $y=\frac 5x$ is a rational equation. The variable $x$ appears in the denominator.
- $y=\frac{1}{5} x$ This looks quite similar to the equation before. But this is also a linear equation.
- $y=x^2-5$ Here the variable $x$ is squared. Thus this is a quadratic equation and therefore not a linear equation at all.
- $y=\sqrt{x}+5$ is a radical equation.
- $y=2x+5$ is a linear equation.
-
Determine which factored equations are linear.
HintsFirst establish each equation in the form $y=...$.
Each linear equation is given by $y=mx+b$.
All variables in linear equations are raised to the power of $1$.
Use the distributive property to multiply, $2(x-2)=(2)(x)-(2)(2)=2x-4$.
For multiplying two binomials you use the FOIL method. Let's have a look at the following example: $(x-1)(x+2)$.
- Multiply the First: $x\times x=x^2.
- Next, multiply the Outer: $x\times 2=2x$.
- Now multiply the Inner: $(-1)\times x=-x$.
- Last, multiply the Last: $(-1)\times 2=-2$.
$(x-1)(x+2)=x^2+2x-x-2=x^2+x-2$.
SolutionWe can write each linear equation in the form $y=mx+b$. Otherwise the equation isn't linear.
$~$
Route 1
$y=2(x+1)-x=2x+2-x=2x-x+2=x+2$ $~~~~~$✓
$~$
Route 2
$y=(2x+1)\times x=(2x)(x)+x=2x^2+x$
This is a quadratic equation.
$~$
Route 3
$y^2=2(x+1)-x$
The right side is the same as that of route number $1$. Finally, we have to take the square root to get
$y=\sqrt{x+2}$
This is a radical equation.
$~$
Route 4
$2\times x\times y=4$
Dividing by $2$ and $x$ we get $y=\frac2x$.
This is a rational equation.
$~$
Route 5
$2x+y=5$
Subtracting $2x$ and arranging the terms in the right order we get
$y=-2x+5$ $~~~~~$✓
$~$
Route 6
$y=(x+1)(x-2)$
Using FOIL-multiplication we get
$y=(x+1)(x-2)=x^2-2x+x-2=x^2-x-2$
a quadratic equation.
-
Determine which statements are true.
HintsHere is a parabola. The corresponding equation is quadratic: $y=2x^2$.
This is an example of a linear equation: $y=2x+4$.
SolutionLinear equations contain variables raised to the power of $1$.
All other equations are nonlinear. When written in simplified form, here are some things that make an equation not linear:
- having a variable in the denominator.
- having a variable under a radical.
- having a variable squared or cubed.
-
Find the corresponding expression and state if it is linear or nonlinear.
HintsEach time assign the variable $x$ to the unknown number first.
To multiply two binomials use the FOIL-multiplication
$(-2x+8)(x+10)$
$=(-2x)(x)-(2x)(10)+(8)(x)+(8)(10)$
$=-2x^2-20x+8x+80$
$=-2x^2-12x+80$
Use the distributive property to get
$2(3x+6)=(2)(3x)+(2)(6)=6x+12$.
Solution$y$ is the product of $7$ and an unknown number.
$7$ times an unknown number can be written as $7x$. So we get
$y=7x$,
which is a linear equation.
$y$ is equal to $5$ multiplied by the reciprocal of the quotient of an unknown number and $12$.
To get the reciprocal you switch the numerator and denominator. With this we can establish the equation as follows:
$y=5\times \frac{12}x=\frac{60}x$
This is a rational equation and thus nonlinear.
$y$ is given as the quantity eight minus twice an unknown number, multiplied by the sum of this unknown and $10$.
Let's do this step by step
- eight minus twice an unknown number is given by the binomial $8-2x=-2x+8$.
- the sum of this unknown and $10$ can be written as $x+10$
$y=(-2x+8)(x+10)=(-2x)(x)-(2x)(10)+(8)(x)+(8)(10)$ $=-2x^2-20x+8x+80=-2x^2-12x+80$,
which is quadratic and thus nonlinear.
$y$ is the sum of four consecutive numbers, the smallest one represented by $x$.
The four consecutive numbers are given as follows
- $x$
- $x+1$
- $x+2$
- $x+3$
This is a linear equation.
$y$ is given by the half of the product of a number multiplied by itself three times.
Multiplying a number by itself can be written with exponents. So a number multiplied itself three times looks like
$x\times x\times x=x^3$
We get $y=\frac12x^3$,
which is a nonlinear equation.
Just one more example and we're done:
Let $y$ be twice the sum of $6$ and $3$ times an unknown number.
First, we establish the sum $3x+6$. Twice this sum is $2(3x+6)$. Putting all this together we can conclude
$y=6x+12$,
which is a linear equation.
















well hello there fellow earthlings
is this the youtube comment section
hi
hi its mr o