Try sofatutor for 30 Days

Discover why over 1.6 MILLION students choose sofatutor!

Writing Equations Using Symbols

Watch videos

Start exercises

Show worksheets
Rating

Ø 4.5 / 2 ratings
The authors
Avatar
Team Digital

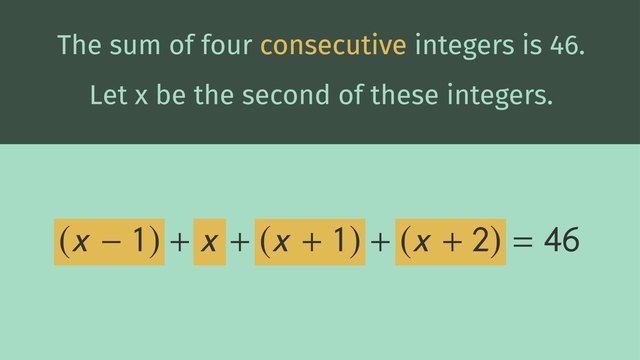
Basics on the topic Writing Equations Using Symbols

After this lesson, you will be able to visualize mathematical statements and translate them into a equation using variables.

The lesson begins by teaching you that mathematical statements can be written in the form of an equation. It leads you to learn how to translate mathematical keywords into variables and operations. It concludes with a note that when writing equations, keywords are the solution!

Learn about writing equations using variables by helping Leyla visualize what she heard from the whispering swamp.

This video includes key concepts, notation, and vocabulary such as the term variable (an unknown quantity usually represented by a letter); consecutive integers (numbers that follow each other in order like 1,2,3, etc.); and math keywords (words which correspond to a mathematical operation or expression).

Before watching this video, you should already be familiar with the different math keywords such as “consecutive integers”, “less than”, “half of the square”, etc.

After watching this video, you will be prepared to learn how to translate verbal phrases into mathematical expressions and solve real-life problems involving a mathematical equation.

Common Core Standard(s) in focus: 8.EE.C.7 A video intended for math students in the 8th grade Recommended for students who are 13-14 years old

Transcript Writing Equations Using Symbols

Leyla and her trusty helperbot, Fridge, have gotten themselves lost on a strange planet once again. This time, they find themselves trudging through a stinking wasteland known as the Whispering Swamps and Fridge has just fallen neck-deep into a cesspool and can’t get out! But maybe they can get some help from this local hermit it seems like he's communicating with the Whispering Swamp somehow. Leyla strains to listen. A number is four times larger than the square of half the number? The hermit seems to be visualizing an equation. If only Leyla could understand the power of Writing Equations Using Variables! Let’s see if we can visualize the equation that Leyla heard. A number is four times larger than the square of half the number. Let’s start with the variables. Are there any values here that are unknown? The swamp is whispering about “a number.” We're not sure what the value of that number is, so let's call it 'x'. In math, the word “is” means equals. So what's 'x' equal to? 4 times' means we're multiplying by four and 'the square of' tells us we're raising an expression to the second power. The remaining expression 'half the number' goes inside the parentheses as 'x' over two. So THAT is what the swamp meant! It looks like solving the puzzle has almost freed Fridge! As the swamp gurgles out another strange sentence, Leyla is ready to visualize the math again! The sum of four consecutive integers is 46. The first step is to identify and define the variable. We have four unknown consecutive integers and we know that their sum is equal to 46. The keyword “sum” means we're going to add. Now, let's start filling in those empty spaces by calling the second integer 'x'. The word “consecutive" means in order, one after another.

Ok, if the second integer is 'x', that means the first integer is one less than 'x'. We can write that as 'x' minus 1. The third number is one more than 'x', or "x plus 1." And that makes the fourth number two more than 'x', or "x plus 2." Now we have an equation which represents the sum of four consecutive integers that equal 46!

To review, we can turn sentences into mathematical equations if we first, identify and define the variables. Ask yourself the question: what are the unknown numbers? Then assign those unknown numbers a variable, like 'x'. Next, look for math-related keywords like known numbers and words that represent operations. Finally, you can write the equation using parentheses to break up complex parts of the sentence.

Leyla is now a true master! Her visualization skills have levitated poor Fridge out of the whispering swamp with a little help from her new friend, of course.

Writing Equations Using Symbols exercise

Would you like to apply the knowledge you’ve learned? You can review and practice it with the tasks for the video Writing Equations Using Symbols.

  • Explain writing equations using variables.
    Hints
    • Variables are unknown values in the equation that are represented by a letter.
    • The word is means equals, sum means add, times means multiply, and square means raise to the power of $2$.

    A number is 3 times larger than the square of one third of a number.

    • The unknown is the number called $x$.
    • is means equals, times means multiply, square means raise $\frac{x}{3}$ to the power of $2$.
    • The equation is $x=3(\frac{x}{3})^{2}$

    The sum of three consecutive integers is $35$.

    • We have three unknown consecutive integers.
    • Let the second unknown integer be $x$.
    • sum means to add, and is means equals.
    • Consecutive means next to one another, so if the second integer is $x$, the first integer is one less than $x$ or $x-1$.
    • The equation is $(x-1)+x+(x+1)=35$

    Solution

    Layla hears the hermit whisper, "A number is four times larger than the square of half the number".

    1. Identify and define the variable.

    • The unknown value is "the number" which we will call $x$. Variables can be defined by any letter in the alphabet, but $x$ is the most common.
    2. Look for math-related keywords.
    • Math-related keywords are words that translate into mathematical symbols.
    • In a math equation, "is" means equals.
    • "4 times" means multiplying by 4.
    • "Square of" means raising the expression to the 2nd power.
    • The remaining expression, $\frac{x}{2}$, which represents half the number, goes inside the parentheses.
    3. Write the equation.
    • Now that you identified the variable and found the math-related keywords, you can translate the sentence into a mathematical equation, $x=4(\frac{x}{2})^{2}$.

    The hermit whispers another equation, "The sum of four consecutive integers is 46".

    1. Identify and define the variable.

    • We have four unknown consecutive integers.
    • Consecutive integers are integers that follow each other in order like, 1,2,3 and 4.
    • Since we would like to represent all of the integers with the same variable, we will begin by letting the second integer be $x$.
    2. Look for math-related keywords.
    • Math-related keywords are words that translate into mathematical symbols.
    • In a math equation, sum means we are going to add.
    • The word consecutive means in order, one after another.
    3. Write the equation.
    • We identified through the math-related keywords that we will be using the addition sign and the equal sign.
    • We also know that $x$ represents the second integer, which means $x-1$ represents the first integer, $x+1$ represents the third integer, and $x+2$ represents the fourth integer.
    • To check this, substitute $x=1$ to see if the expressions translate into four consecutive integers: $x-1$ is $0$, $x$ is $1$, $x+1$ is $2$, and $x+2$ is $3$. Since $0$,$1$,$2$ and $3$ are four consecutive integers, we know that the expressions are correct.
    • Therefore, we can combine the math-related keywords with our expressions for consecutive integers to write the equation, $(x-1)+x+(x+1)+(x+2)=46$

  • Write expressions using variables.
    Hints

    To translate a statement into an algebraic equation:

    1. Identify and define the variable with a letter. Ask yourself, what is the unknown value?
    2. Find key math words. For example, is means equals.
    3. Write the equations.

    Two times the quotient of a number and four is sixteen.

    • The variable is a number that we will call $x$.
    • times means multiply, quotient means divide, is means equals.
    • The equation is, $2(\frac{x}{4})=18$

    Two times the sum of a number and four is sixteen.

    • The variable is a number that we will call $x$.
    • times means multiply, sum means add, is means equals.
    • The equation is, $2(x+4)=16$

    Solution

    To turn a sentence into a mathematical equation:

    1. Identify and define the variable.
    2. Find key math words.
    3. Write the equations.
    1. Three minus a number is seven.
    • The variable is a number that we will call $x$.
    • minus means subtract, is means equals.
    • The equation is, $3-x=7$
    2. The sum of a number and three is seven.
    • The variable is a number that we will call $x$.
    • sum means add, is means equals.
    • The equation is $x+3=7$
    3. Seven times the quotient of a number and two is eighteen.
    • The variable is a number that we will call $x$.
    • times means multiply, quotient means divide, is means equals.
    • $7(\frac{x}{2})=18$
    4. Seven times the sum of a number and two is eighteen.
    • The variable is a number that we will call $x$.
    • times means multiply, sum means add, is means equals.
    • The equation is $7(x+2)=18$
    5. Five less than two times a number is twenty-six.
    • The variable is a number that we will call $x$.
    • less means subtract, times means multiply, is means equals.
    • $2x-5=26$
    6. Two times a number minus five is twenty-six.
    • The variable is a number that we will call $x$.
    • times means multiply, minus means subtract, is means equals.
    • The equation is, $2x-5=26$

  • Identify math keywords and the algebraic equation corresponding to the given sentence.
    Hints
    • To find the word that represents the variable, look for the the unknown value.
    • To find the key math words, look for words that represent math operations. For example, times means multiply.
    • To find the correct algebraic equation, look for the equation that represents the unknown variables and the key math words.

    Seven times a number is five more than ten.

    • a number is the word that represents a variable.
    • times, is, and more are key math words.
    • The equation is $7x=5+10$

    Three times five divided by a number is twenty-two.

    • a number is the word that represents a variable.
    • times, divided, and is are key math words.
    • The equation is $3(\frac{5}{x})=22$

    Solution

    1. Three times a number is five less than twelve.

    • The variable highlighted in green is a number because it is the unknown value.
    • The math key words highlighted in purple are times, is, and less. Times means multiply, is means equals, and less means subtract.
    • The equation highlighted in blue is $3x=12-5$
    2. Double the quotient of a number and three is fourteen.
    • The variable highlighted in green is a number because it is the unknown value.
    • The math key words highlighted in purple are double, quotient, and is. Double means multiply by 2, quotient means divide, and is means equals.
    • The equation highlighted in blue is $2(\frac{x}{3})=14$
    3. Three increased by four times a number is twenty decreased by four.
    • The variable highlighted in green is a number because it is the unknown value.
    • The math key words highlighted in purple are increased, times, is, and decreased. Increased means add, times means multiply, is means equals, and decreased means subtract.
    • The equation highlighted in blue is $3+4x=20-4$

  • Write the algebraic equations corresponding to the given statement.
    Hints

    To represent consecutive even integers in an algebraic equation, let $x$ be your first integer. Consecutive means next to each other, and even means every other number, so the next even integer would be $x+2$ followed by $x+4$, and so on.

    You may find it helpful to break the statement into three parts and carefully interpret each and every word.

    • A number plus seven is the square of the difference of the number and three.
    • A number plus seven is $x+7$.
    • is means equals.
    • the square of the difference of the number and three is $(x-3)^2$.
    • So we have that the corresponding equation is: $x+7=(x-3)^2$

    Quotient means divide and product means multiply.

    • The quotient of a number and seven is the product of three and twenty-one.
    • The quotient of a number and seven is $\frac{x}{7}$.
    • is means equals.
    • the product of three and twenty-one is $3(21)$.
    • So we have that the corresponding equation is: $\frac{x}{7}=3(21)$

    Solution

    To translate a statement into an algebraic equation:

    1. Identify and define the variable with a letter. Ask yourself, what is the unknown value?
    2. Find key math words. For example, is means equals.
    3. Write the equations.
    1. The sum of two consecutive even integers is fifteen.
    • The variable is an integer that we will call $x$.
    • Consecutive means next to each other, and even means every other number, so the next even integer would be $x+2$.
    • sum means add, and is means equals.
    • The equation is: $x+(x+2)=15$
    2. A number minus fifteen is the square of the sum of a number and two.
    • The variable is a number that we will call $x$.
    • minus means subtract, is means equals, square means raise to the power of $2$, and increased means add.
    • The equation is: $x-15=(x+2)^2$
    3. The product of two consecutive even integers is fifteen.
    • The variable is an integer that we will call $x$.
    • Consecutive means next to each other, and even means every other number, so the next even integer would be $x+2$.
    • product means multiply, and is means equals
    • The equation is: $x(x+2)=15$
    4. The quotient of a number and five is half of the product of three and 6.
    • The variable is a number that we will call $x$.
    • quotient means divide, is means equals, and product means multiply.
    • The equation is: $\frac{x}{5}=\frac{1}{2}(3\cdot 6)$
    5. The product of a number and five is six divided by three.
    • The variable is a number that we will call $x$.
    • product means multiply, is means equals.
    • The equation is: $5x=\frac{6}{3}$
    6. A number plus fifteen is two less than twice the number.
    • The variable is a number that we will call $x$.
    • plus means add, is means equals, less means subtract, and twice means multiply by $2$.
    • The equation is: $x+15=2x-2$

  • Assign words to their corresponding mathematical symbol.
    Hints
    • Increase means to make greater in size.
    • Decrease means to become smaller in size.

    A number that is tripled is represented by $3(x)$.

    To cut in half, means to divide by $2$.

    Solution

    1. $+$

    • Increase means to make greater in size.
    • Sum is the result of adding numbers.
    2. $-$
    • Decrease means to become smaller in size.
    • Difference is the result of subtracting one number from another.
    3. $2(x)$
    • Doubled means to multiply by $2$.
    • Twice means to multiply by $2$.
    4. $\frac{x}{2}$
    • Quotient is the answer after you divide one quantity by another.
    • Half means to divide by $2$.

  • Translate the word problems into algebraic equations.
    Hints

    To translate a statement into an algebraic equation:

    1. Identify and define the variable with a letter. Ask yourself, what is the unknown value?
    2. Find key math words. For example, is means equals.
    3. Write the equations.

    Ebony spent half of her weekly allowance at the mall. To earn more money, her parents let her wash the car for $4$ dollars. What is her weekly allowance if she has $12$ dollars?

    The equation is: $\frac{1}{2}x+4=12$

    Ebony spent the square of her weekly allowance at the mall. She also owed her parents $4$ dollars. What is her weekly allowance if she has $12$ dollars?

    The equation is: $x^2-4=12$

    Solution

    To translate a statement into an algebraic equation:

    • Identify and define the variable with a letter. Ask yourself, what is the unknown value?
    • Find key math words. For example, is means equals.
    • Write the equations.
    1. Omar earned double the amount of money that he earned last year, plus an additional $350$ in tips. How much did Omar make if his total salary was $750$?

    • Let $x$ be the amount of money Omar earned last year.
    • The equation is: $2x+350=750$
    2. Kai is buying a new phone. The cost of a phone is $750$ dollars but the phone company is offering a special for $2$ dollars off every day of the new contract. If the total price is $350$ dollars, how many days is Kai's new phone contract?
    • Let $x$ be the number of days.
    • The equation is: $750-2x=350$
    3.Raquel is three years older than his sister's age squared. Raquel is $18$. How old is his sister?
    • Let $x$ be the age of Raquel's sister.
    • The equation is: $3+x^2=18$
    4. Steven likes to bake cookies. He bakes a total of $24$ cookies and gives half to a neighbor. How many cookies does Steven have left?
    • Let $x$ be the number of cookies.
    • The equation is: $\frac{1}{2}x=24$
More videos in this topic Writing and Solving Linear Equations
video image

Writing Equations Using Symbols
video image

Linear and Nonlinear Expressions
video image

Writing and Solving Linear Equations
video image

Classifying Solutions of Linear Equations
video image

Linear Equations in Disguise

video image

Problem Solving with Multi-Step Equations
Company
Platform
How it works
Help
Legal
Carbon neutral, Company, ClimatePartner.com/14808-2007-1001
Any questions? Contact us!
Any questions? Contact us!
Confirm cookie settings

We use our own cookies, third-party cookies and similar technologies on our website. Some of these are necessary to ensure that you can use our platform securely. Others are not absolutely necessary, but help us, for example, to evaluate and improve the use of our website. A distinction is made between „Necessary cookies“, „Functionality & Comfort“, „Statistics & Analysis“ and „Marketing“. Marketing cookies are also used for ads personalisation. This also involves setting cookies from Google (Google's privacy policy). Further information can be found in our Privacy Policy and Cookie Details.

To consent to the use of non-essential cookies, click on „Accept all cookies“. Or you can make an individual selection under „Adjust cookies individually“. There you will also find further information on the purposes and third-party providers used. If you allow these, your consent also includes the transfer of data to third countries that do not have a level of data protection comparable to that in the EU and/or the UK. By clicking on „Reject all“, only necessary cookies are set. You can change or revoke your selection at any time.

Are you under 13 years old? Then please click „Reject all“ or get consent from your legal guardian.

Contact Us
More information

These cookies are absolutely necessary for the secure use of our website and the provision of our services. They enable basic functions and cannot be deselected. Only own cookies are set.

More information

We use our own cookies to provide some of the convenience functions of our learning platform and to continuously optimise our website.

More information

Cookies for statistical and analytical purposes help us to understand how our website is used. They are used in particular to evaluate and optimise our learning platform, our content and our offers. In addition to our own cookies, cookies are also set by the following third-party providers Google Analytics, Amplitude, Convert and Hotjar.

More information

Marketing cookies are set by us or our partners on our website to build a profile of your interests and show you relevant content on our and third party websites. We also use these cookies to measure, monitor and control our marketing activities. In addition to our own cookies, cookies are also set by the following third-party providers: Google, Bing,, Facebook, Taboola, Outbrain, Doubleclick, YouTube, Pinterest, TikTok, Snapchat Ads, LinkedIn Ads, X (former Twitter), Reddit.

Contact Us Privacy Policy