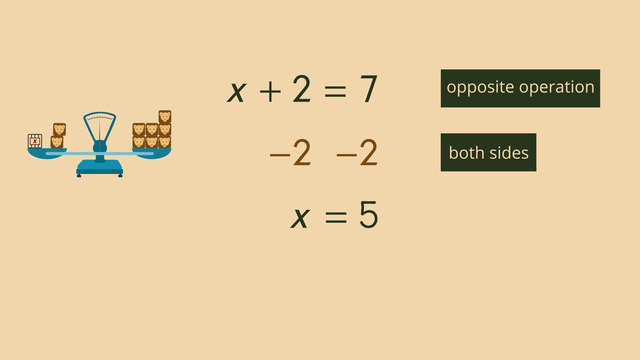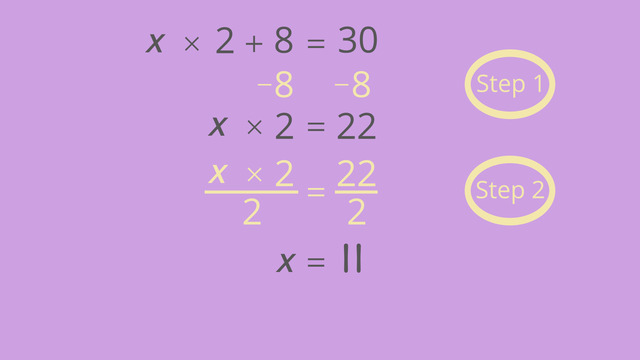Distance - Rate - Time – Same Direction
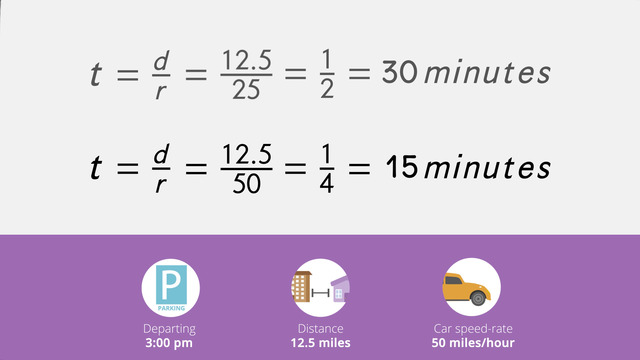

Basics on the topic Distance - Rate - Time – Same Direction
In the real world, calculating distance, rate, and time problems is a real problem. How far, how long, and how much time – these are questions people must solve every day but in the real world, the problems are not presented with an equation, so we need to know how to write an equation to solve the problem.
To solve these types of problems, remember to use the DRT triangle. The triangle helps us remember the formula distance is equal to rate times time. We can modify the equation and create two other equations: rate is equal to distance divided by time, and time is equal to distance divided by rate.
The triangle is a useful graphic reminder. The D is on the top, and R and T make up the base. How do we know which form of the DRT formula to use? Look to the word problem for the answer. What is the unknown amount? Select the formula that solves for that specific unknown amount.
Watch this video and see how important it is to understand how to solve distance-rate-time problems. You might also learn a valuable lesson on what not to do in school.
Rearrange formulas to solve for unknown values. CCSS.MATH.CONTENT.HSA.CED.A.4
Transcript Distance - Rate - Time – Same Direction
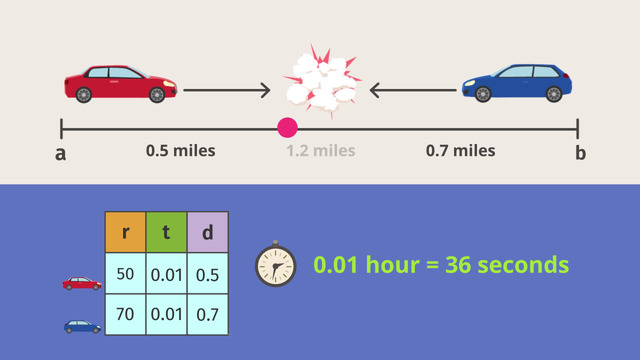
Tom is in big trouble. Two days ago, he pranked his teacher Ms.Trunchbull. Now there is a letter from his teacher waiting in his mailbox at home. He doesn't want his mother to see the letter. So time is ticking.
His mom, working across from the school, finishes work in half an hour, at 3 pm. Tom has to beat his mom! This is a Distance-Rate-Time-Problem. Will he be able to make it?
Tom's school bus leaves school at 2:50 pm. The distance between school and mom's work and Tom's home is 12.5 miles. The school bus drives at an average speed of 25 miles per hour. His mother is a very fast driver and drives by car at an average of 50 miles per hour.
Solving Distance-Rate-Time Problems
You know that rate is distance divided by time. For example: miles per hour. When you are solving distance-rate-time problems, you can use this triangle for help.
- As you can see, it shows that rate, "r", equals distance, "d" over time, "t", because the "d" is on top of the "t".
- It also shows you that "t" equals "d" over "r", because the "d" is on top of the "r".
- Lastly, because the "r" and "t" are on the same level, "d" equals "r" times "t".
For this problem you are trying to solve for time, "t". So you need to use the "t" equals "d" over "r" form of the formula. The time it takes Tom to get home equals the distance, 12.5 miles, divided by the rate, 25 miles per hour,
You can reduce this to 1 over 2. This means, it takes Tom half an hour to get home. So let's calculate how long it takes Tom's mom to drive home. You again need the formula time is distance over rate. She drives 50 miles per hour to get home.
The distance is the same as in the previous calculation. To solve for t, you should divide 12.5 by 50. You can reduce this to one fourth. So it will take Tom's mom 15 minutes to get home.
Since Tom leaves school at 2:50 pm and it takes him half an hour to get home, he should arrive home at 3:20 pm. Tom's mom leaves work 10 minutes later at 3:00, this means that she will get home at 3:15. Oh no! Tom's mom is going to beat Tom by 5 minutes!
Distance - Rate - Time – Same Direction exercise
-
Identify all forms of the equation used to solve the distance-rate-time problem.
HintsLook at this triangle:
- $d$ is above $t$ and $r$
- $r$ and $t$ are on the same level
If you know one version of the distance-rate-time equation, manipulate it using inverse operations so that you isolate each variable on the left side of the equation.
SolutionYou can use the triangle on the right to help you remember the equations concerning the distance-rate-time problem.
- Rate is distance divided by time, $r=\frac dt$ because you have to divide distance by time to get the rate. Also, notice that the $d$ is above the $t$ in the provided figure.
- You can transform $r=\frac dt$ by multiplying both sides of the equation by $t$ and then dividing both sides by $r$ to isolate the $t$, giving us $t=\frac dr$. Notice that the $d$ is above the $r$ in the triangle.
- Multiplying $t=\frac dr$ by $r$ gives us our final equation: $d=r\times t$. $r$ and $t$ are on the same level in the triangle.
-
Set up an equation to see if Tom arrives earlier than his mom.
HintsYou can transform the equation to fit your needs by manipulating the equation shown here using multiplication and division.
Calculate the time the school bus takes to bring Tom home and add this to Tom's starting time.
Solve the problem in a similar manner for Tom's mom.
There exist three variations of distance-rate-time equation:
- $t=\frac dr$
- $r=\frac dt$
- $d=t\times r$
Remember, the units for time need to be consistent in your calculations. For example, if you are calculating miles per hour, you should not use minutes without converting minutes to hours.
SolutionTom played a prank on his teacher and needs to intercept the letter his teacher sent home before his mom gets a chance to read it.
What we know:
- Tom's starting time, $2:50$ pm, and Tom's mom's starting time, $3:00$ pm
- The distance between Tom's school and home and the distance between Tom's mom's work to home is the same: $12.5$ miles
- The rate of Tom's school bus, $25$ miles per hour, and the rate of Tom's mom's driving, $50$ miles per hour
- First, we want to calculate the time it takes Tom to get home: $t=\frac{12.5}{25}=0.5$ hours. Since $1$ hour is $60$ minutes, we have to add $0.5 \times 60$ minutes to Tom's starting time to get his arrival time: $3:20$ pm.
- Then, we evaluate the time it takes Tom's mom to get home: $t=\frac{12.5}{50}=15$ minutes. We also have to add this time to Tom's mom's starting time to get her arrival time: $3:15$ pm.
-
Calculate the time Tom's mom takes to drive home if she drives $37.5$ miles per hour.
HintsUse the equation $\large{t=\frac dr}$ to compute the time it takes for Tom's mom to drive home.
The result is a fraction. Convert your answer into minutes.
For example:
- $\frac12$ hours is the same as $\frac 12\times 60=30$ minutes
- $\frac 15$ hours is the same as $\frac15\times 60=12$ minutes
Add your answer to the starting time to get the arrival time.
SolutionWe have the following information:
- The distance from Tom's mom's work to home: $12.5$ miles
- Tom's mom drives at a rate of $37.5$ miles per hour
- Tom's mom's starting time: $3:00$ pm
- We're looking for the time it takes Tom's mom to drive home using the equation: $t=\frac dr$.
- Plugging in the values gives us $t=\frac{12.5}{37.5}=\frac13$ hours.
- To convert $\frac13$ hours to minutes, we have to multiply $\frac 13$ by $60$, giving us $20$ minutes.
- We get Tom's mom's arrival time by adding $20$ minutes to her starting time: $3:00 + 0:20 = 3:20$ pm.
-
Find the distance each friend has to travel to arrive at the movies.
HintsThink about which of the following forms of the distance-rate-time equation you need to use:
- $r=\frac dt$
- $t=\frac dr$
- $d=t\times r$
Think about the information you already have:
- The time it takes each friend to get to the theater
- The rate of travel for each of the friends
Convert the time in minutes to hours.
For example: $15$ minutes corresponds to $\frac{15}{60}=\frac14$ hours.
SolutionWe have to calculate the distances Tom and each of his friends need to travel to get to the theater. For every friend, including Tom, we have two pieces of information:
- the time it takes each friend to get to the theater
- the rate of travel for each friend
Because the unit of measure for rate is miles per hour, we first have to convert minutes into hours.
- Tom walks $20$ minutes at a rate of $3$ miles per hour.
- Anne takes $0.5$ hours by bus at a rate of $30$ miles per hour.
- Paul rides his bike $10$ minutes at a rate of $12$ miles per hour.
- George also rides his bike $20$ minutes at a rate of $15$ miles per hour.
- Tom's distance is $d=\frac13\times 3=1$ mile because $20$ minutes corresponds to $\frac{20}{60}=\frac 13$ hour.
- Anne travels by bus at $30$ miles per hour for $0.5$ hours. We have to evaluate $d=\frac12\times 30$, which means Anne traveled $15$ miles.
- Paul rides his bike for $10$ minutes, or $\frac{10}{60}=\frac 16$ hours. So Paul's distance is given by $d=\frac16\times 12$, which means Paul rode his bike for $2$ miles.
- George rode his bike a bit faster than Paul at $15$ miles per hour. He also rode a little longer than Paul did. If we convert minutes to hours, we get $\frac{20}{60}=\frac 13$ hour. That means Paul rode for $d=\frac13\times 15$ miles, or $5$ miles.
-
Describe the correlation between distance, rate, and time.
HintsConvert minutes to hours:
- $15$ minutes is $0.25$ hours
- $30$ minutes is $0.5$ hours
Pay attention to the units of measure:
- Time is measured in minutes or hours
- Distance is measured in miles
- Rate is measured in miles per hour, or mph
SolutionLooking at the triangle on the right, we can establish the following equations:
- $t=\frac dr$
- $r=\frac dt$
- $d=t\times r$
If we're looking for the rate of Tom's mom, since she drives $12.5$ miles in $15$ minutes, we have to use the second equation. First, we have convert $15$ minutes to $0.25$ hours. This gives us $r=\frac{12.5}{0.25}=50$ mph.
If Tom's school bus drives $25$ miles per hour for $30$ minutes, he will cover a distance of $12.5$ miles. For this question we need the third version of this equation. First, we have to convert $30$ minutes to $0.5$ hours. This leaves us with $d=0.5\times 25=12.5$ miles.
-
Determine the time Tom needs to leave home in order to get to school on time.
HintsThe information we're given is:
- The rate Tom rides his bike: $12$ miles per hour
- The distance to Tom's school: $8$ miles
We are interested in how much time it takes Tom to get to school. Therefore, we can use $\large{t=\frac dr}$.
Subtract the time it takes Tom to get to school from Tom's school's starting time, $8$ am.
To convert hours into minutes multiply the fraction of an hour by $60$ minutes.
SolutionTom's school starts at $8$ am. When must he leave his home to arrive at school on time?
We know that Tom bikes at an average rate of $12$ miles per hour. The distance to his school is $8$ miles. We need to know how long it takes Tom to get from home to his school.
First of all, we have to decide which equation we need. We have to use $t=\frac dr$ because we know Tom's distance as well as his rate. We are looking for time.
When we organize our given information we get:
- $r=12$ miles per hour
- $d=8$ miles
In order to calculate Tom's starting time, we have to subtract $40$ minutes from $8:00$ am. Since there are $60$ minutes in an hour, Tom must leave at $7:20$ am if he doesn't want to be late for school.