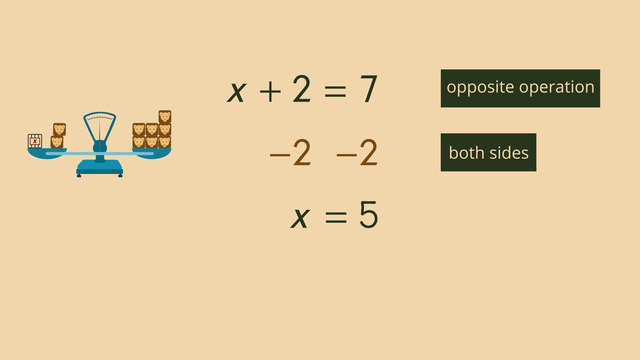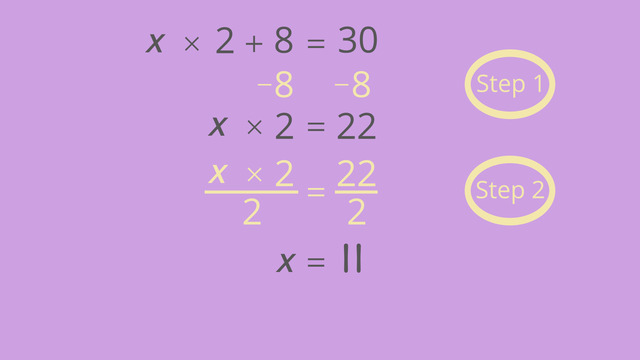Distance - Rate - Time – Different Directions

Basics on the topic Distance - Rate - Time – Different Directions
A boat departs from London and travels at a certain speed, and another boat leaves from Amsterdam. The two boats travel on the same path but in the opposite direction… Does this problem make you seasick? Don’t worry, it’s a distance-rate-time problem with travel from different directions.
Use the distance-rate-time formula to solve this kind of problem. The DRT triangle can help you remember the three formulas used to solve problems of how far, how fast, and how long. Distance is equal to rate times time, rate is equal to distance divided by time, and time is equal to distance divided by rate. Which formula you should use depends on which quantity is unknown.
Distance, rate, and time problems when travel is from different directions won't be complicated as long as you stay organized, set up a table and enter all the information you know, and use variables to represent the unknown values. Be careful when using different units of time. You cannot calculate minutes and hours in the same problem, so before calculating the distance, rate, or time, convert minutes to hours or hours to minutes.
To learn more about how to calculate the distance, rate, or time of travel from different directions, watch this video and see how Johnny Crash uses the DRT formulas to solve his problems.
Create equations that describe numbers or relationships. CCSS.MATH.CONTENT.HSA.CED.A.1
Transcript Distance - Rate - Time – Different Directions
Tim Carcrashian, true to his name, works for a vehicle crash testing company. His job is to set up the slow-motion-camera used to document car crashes. The set-up of the camera is very expensive and time-consuming. To do the job just right, Tim needs to know exactly when and where the cars will crash. How can we help him?
The distance-rate-time pyramid
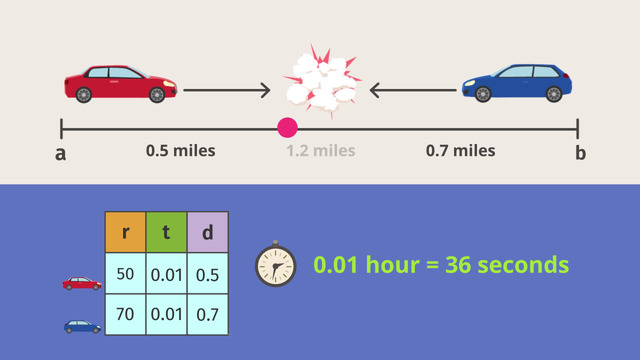
This is a distance-rate-time problem - with cars coming from different directions. For the test crash, Car 1 and Car 2 will drive towards each other. Car 1 will pass Point A going 50 miles per hour, and Car 2 will pass Point B going 70 miles per hour. The distance from Point A to Point B is 1.2 miles.
Exactly where and when will the cars crash? Let’s figure out how to solve this problem. Distance is equal to rate times time. This pyramid can help us remember the formula. A shorter, more common, way to say this d = rt.
Write equations
Ok, let's get started...It's a good idea to use a table to organize the data. First, let's fill in the values with what we already know, the rate for each car. We don’t know the value for time yet, just that it's the same for both cars, so for now, we can represent this with the variable, 't'. We can write two equations to describe what's going on here: d = 50t. And...d = 70t.
Let's write that information into the table. Since we know the total distance the two cars will a travel together is 1.2 miles, we can set up an equation and solve for the unknown time. 1.2 = 50t + 70t. Evaluating this we get: t = 1/100 of an hour. Let's fill in the table... Now, we can use the value we just calculated for the time to determine the actual distances both cars will drive before crashing and fill in the table.
d = 50(0.01), which is equal to 0.5
d = 70(0.01), giving us 0.7
The distance-rate-time formula
This is just great! Tim is so happy! Using the distance-rate-time formula, coming from different directions, now, Tim knows Car 1 will drive exactly 1/2 of a mile and Car 2 will drive 7/10 of a mile, then crash, bang, boom! As a bonus, Tim also knows exactly when this will happen. The cars will crash after 36 seconds, which is equal to 1/100 of an hour. He sets up the Slow-Motion-Camera Unit just right. He’s so good at his job, maybe he'll get a promotion and a big raise!
Oh no. One week later, Tim learns the test track will be under construction in order to improve the testing conditions. During construction, the right side of the track will be shortened. Instead of the track having a distance of 1/2 of a mile on the left side and 7/10 of a mile on the right side...
Calculate a new rate
The right side will be only 4/10 of a mile long. Tim doesn't want to change the set-up of the camera. What can he do so the cars will still crash at the same place and time? He can't change the distance or the time, but he can change the speed of Car 2. Let's calculate the new rate using the distance-rate time formula.
As before, we have d = rt. To isolate the rate, divide distance by time. r = 0.4 / 0.01. The rate is 40 miles per hour. So, if Car 2 travels on the track at a rate of 40 miles per hour for 4/10 of a mile, after 1/100 of an hour, the two cars will crash in just the right spot.
Change the distance
Another week goes by... Tim gets an email... The track improvements are all done, and the new plan is to crash test one of the cars driving at a very high speed. Car 2 will be tested driving 90 miles per hour. Tim doesn't have time to change the camera. What should he do? He can't change the speed or the time, but he can change the distance Car 2 will drive.
If Car 2 drives 90 miles per hour for 1/100 of an hour, use the distance-rate-time formula to calculate the new distance it must drive so the camera can capture the crash. Let's reuse our formula from before: distance is equal to rate times time. 90(0.01) = 0.9 miles. So Tim can get the perfect camera shot, Car 2 must drive 9/10 of a mile at 90 miles per hour for 1/100 of an hour .
Summary
Let's summarize: The distance-rate-time pyramid is a handy graphic organizer to help you remember and understand how to solve these kind of problems. t = d/r, r = d/t, d = rt. After all his hard work, Tim can finally watch the crash test. Oh no, that's not test Car 2...That looks a lot like Tim's boss' car...
Distance - Rate - Time – Different Directions exercise
-
Determine when and where the car will crash.
HintsFill in the table:
$\begin{array}{|l|c|c|c|} \hline &r&t&d\\ \hline \text{car 1}&50&t&?\\ \hline \text{car 2}&70&t&?\\ \hline \end{array}$
Don't forget the mnemonic device.
Determine the unknown quantity, and use the appropriate equation:
- $d=r\times t$
- $r=\frac dt$
- $t=\frac dr$
The sum of the distances is equal to $1.2$ (miles).
SolutionThe red car travels at $50$ mph, while the blue car travels in the opposite direction at $70$ mph.
This is a distance-rate-time-problem with different directions.
Let's start with a table:
$\begin{array}{|l|c|c|c|} \hline &r&t&d\\ \hline \text{car 1}&50&t&50t\\ \hline \text{car 2}&70&t&70t\\ \hline \end{array}$
Use the equation $d=r\times t$.
Since the car cannot travel a distance greater than $1.2$ miles, we write the equation:
$\begin{array}{rclcl} 50t+70t & = & 1.2 &&|\text{Combine Like Terms} \\ 120t&=&1.2 \\ \color{#669900}{\div120} && \color{#669900}{\div120} &&|\text{Opposite Operations} \\ t &=& 0.01 \end{array}$
$t=0.01$ is the time in hours. If we want to know how many seconds this is, we can calculate the conversion. There are $60$ minutes in an hour and $60$ seconds for every minute. Multiply... there are $3,600$ seconds in one hour.
$\begin{array}{rcll} \dfrac{60 ~\text{min.}}{1 ~\text{hr.}} \times \dfrac{60 ~\text{sec.}}{1 ~\text{min.}} &=& \dfrac{3,600 ~\text{sec.}}{1 ~\text{hr.}} \end{array}$
$~$
$\dfrac{3,600 ~\text{ sec.}}{1 ~\text{ hr.}}\times 0.01 ~\text{ hr.} = 36 ~\text{ sec.}$
Now we know that the crash will happen after $36$ seconds.
To find out where the crash will occur, we use the equation $d=r\times t$. Plugging in the known values gives us:
$d = \dfrac{50 ~\text{mi.}} {\text{hr.}} \times 0.01 ~\text{hr.} = 0.5~\text{mi.}$ for the red car
$d = \dfrac{70 ~\text{mi.}} {\text{hr.}} \times 0.01 ~\text{hr.} = 0.7~\text{mi.}$ for the blue car
To document the crash, Johnny has to set up the camera $0.5$ miles far away from Point A.
-
Calculate the rate at which the car travels.
HintsKeep this triangle in mind - it's magic.
If it takes $0.5$ hours to travel a distance of $30$ miles, the rate is $60$ mph.
SolutionYou can remember the formulas by using the Distance Rate Time Triangle.
Here we know
- Time: $t=0.01$ hours
- Distance: $0.4$ miles
By plugging in the known values, we get:
$r=\frac{0.4~\text{mi.}}{0.01~\text{hr.}}=40 ~\text{mph.}$
-
Evaluate the time, if the rate changes.
HintsFirst gather all given information:
- $r=80$
- $t=0.01$
Decide which formula to use.
If you already know the rate and the time, use $d=r\times t$ to find the distance.
For example:
The given information:
- $r=90$
- $t=0.01$
$d = rt$ $d=90\times 0.01=0.9$ miles
SolutionThe speed of the blue car is increased to $80$ mph.
Johnny's a bit lazy and doesn't want to change the camera position. He can't change the rate or the time, but he can change the distance: To figure this out, use the equation: $d=r\times t$.
Given:
- Rate: $80$ mph
- Time: $0.01$ hrs.
So the blue car must be a distance of $0.8$ miles from the crash point. The distance between the two cars at the start is $0.5+0.8=1.3$ miles.
-
Find out when and where the two brothers will meet.
HintsThis is a distance, rate, and time problem with different directions.
Use the formula $d=r\times t$.
Keep in mind that the sum of the distances traveled is $3$ miles.
Use the opposite operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
You have to calculate the time first, and then you can calculate the distance.
SolutionEugene is riding his bike at a rate of $10$ mph, while Shane is running at a rate of $2$ mph.
Here we have a distance rate time problem involving different directions.
First let's consider the distance. We know that $d=r\times t$, and the time $t$ is unknown.
- $d=10t$ for Eugene
- $d=2t$ for Shane
$10t+2t=3$
Combine the like terms: $12t=3$. Finally, divide by $12$: $t=\frac3{12}=\frac14=0.25$ hours.
So the brothers will meet after $0.25$ hours or $15$ minutes.
To determine the distance each boy will travel, we use the formula $d=r\times t$ once again:
- Eugene: $d=10\times 0.25=2.5$ miles
- Shane: $d=2\times 0.25=0.5$ miles
- We know that the brothers will meet after 15 minutes.
- Eugene starts $2.5$ miles away from the meeting point.
- Shane starts $0.5$ miles away from the meeting point.
-
Summarize the distance, rate, and time problem.
HintsUse the magic triangle:
- $d$ over $r$ as well as $d$ over $t$
- $r$ and $t$ on the same level
Remember what the variables stand for:
- Distance
- Rate
- Time
SolutionTo solve problems, use the Distance Rate Time triangle.
- Distance
- Rate
- Time
-
Determine when Jim has to leave his home to make it to his appointments on time.
HintsFirst determine the time, $t$, Jim needs to travel each distance. You should use the following equation:
$t=\frac dr$
Next, calculate the time in hours. Convert to minutes if necessary.
Subtract your answer from the time Jim plans to arrive at each destination. Remember, there are $60$ minutes in an hour.
SolutionWhat do we know?
- The distance from Jim's house to each destination
- Jim's walking rate is $2$ mph
School Distance = $0.8$ miles
$t=\frac{0.8}{2}=0.4$ hours. Multiply by 60: $t=0.4\times 60=24$ minutes.
Subtract $24$ minutes from the arrival time:
$8:00-0:24=7:36$ a.m.
To get to school on time, Jim has to leave his house by $7:36$ a.m.
Grandma's House Distance = $1$ mile
$t=\frac{1}{2}=0.5$ hours. Again, multiply by $60$: $t=0.5\times 60=30$ minutes.
Subtracting $30$ minutes from the arrival time gives us:
$10:00-0:30=9:30$ a.m.
Jim has to leave by $9:30$ a.m. to get to his grandma's house by $10:00$ a.m.
Jack Distance = $3$ miles
$t=\frac{3}{2}=1.5$ hours or, $1$ hour and $30$ minutes.
Subtract this time from the arrival time (We used the $24$-hour clock for convenience.):
$14:00-1:30=12:30$, or 12:30 pm.
Jim has to leave by 12:30 p.m. to meet Jack at $2$ p.m.
Cinema Distance = $4$ miles
Oh, what a day. Jim deserves a little bit of time to kick back and relax. To get to the movies on time, he has to start $t=\frac42=2$ hours before the film starts playing. So he should leave his house at $6$ p.m. He walks $2$ hours to watch a movie!? I hope it's a good movie!