Computing Actual Lengths from a Scale Drawing


Basics on the topic Computing Actual Lengths from a Scale Drawing
After this lesson, you will be able to compute actual lengths represented in a scale drawing by using the scale ratio rather than the scale factor.
The lesson begins by teaching you the difference between a scale and scale factor. It leads you to setting up a proportion using the scale ratio as a fraction. It concludes with solving proportions for an unknown number using cross multiplication.
Learn about computing lengths using scale ratios by helping Frank find Adventure Mike in Siberia!
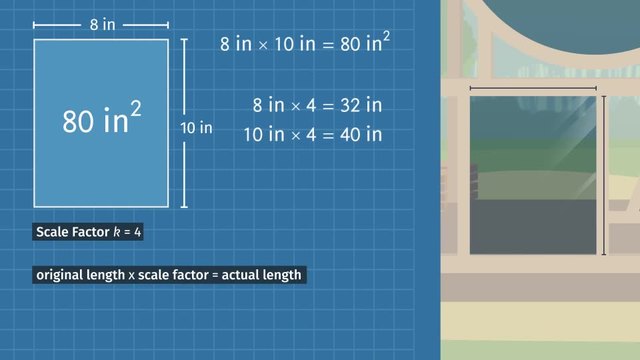
This video includes key concepts, notation, and vocabulary such as the term scale or scale ratio (a type of ratio in which the units are mixed, ie. Inches to miles, cm to km); how to read scale ratio notation (1 cm represents 20 m or 1:20 which is read 1 to 20); and the term scale factor (the constant of proportionality k in the equation y=kx where x is a length in the original image and y is the length in the scaled image).
Before watching this video, you should already be familiar with scale factors, multiple units of measurement (metric and imperial units), and cross-multiplication.
After watching this video, you will be prepared to learn to compute the actual areas represented by scale drawings.
Common Core Standard(s) in focus: 7.G.A.1 A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
Transcript Computing Actual Lengths from a Scale Drawing
Frank the Insurance Man is on his way to Siberia to locate his most important and "eccentric" client, Adventure Mike. Adventure Mike sent Frank an urgent memo, requesting next-day delivery of a large, mysterious package. It's an unusual request for an insurance salesman, but according to the map Mike sent, it’s a straight shot from the airport to his underground location. So what could go wrong? To interpret this map and find Adventure Mike, we'll just need to help Frank compute actual lengths from a scale drawing. Frank's plan is to rent a snow mobile to ride out from the airport to Adventure Mike's location. But the rentals only have enough fuel to take him 35 miles. Will he make it to Adventure Mike? Let's take a closer look at this map and find out. It says here that the map has a scale of 1 inch to 5 miles. Wait, is "scale" the same as "scale factor"? You already know about scale factor, or the constant of proportionality between two related geometric figures. Because scale factors use a fixed multiplier, 'k,' they always use the same unit of measurement to create enlargements or reductions. A scale, however, is a ratio which compares the size of a model to the real-world figure it represents. Like here, where 1 inch on the map represents 5 miles in Siberia. Scales often use mixed units like this, so small measurements can represent huge distances in real life. To represent this same relationship using a scale FACTOR comparing inches to inches, we would need to have a constant of proportionality equal to 158,400. So let's analyze the map using the more useful SCALE of 1 inch to 5 miles. Using a ruler to measure the distance on the map, we can see that Adventure Mike's location is 6.5 inches from the airport. So how can we find out how many miles this represents? Since we know the scale, which is the ratio of 1 inch to 5 miles, we can set up a proportion to find an equivalent ratio which uses 6.5 inches and an unknown number of miles, 'x'. Using cross-multiplication, we get 'x' is equal to 5 times 6.5, or 32.5. So the caves are 32 and a half miles away, just under Frank's 35 mile limit! With a full tank of gas, Frank is off to find Adventure Mike! As he arrives at the location, it looks like Mike left behind another map to help Frank find him. This map has a scale of three quarters of an inch to five eighths of a foot, and Mike's location is marked with an 'x'. Frank is prepared with 40 feet of rope, so he won't lose his way in the darkness. Is that long enough for Frank to find Adventure Mike? To figure that out, let's measure on the map the distance from the entrance of the cave to the 'x'. Then we can convert that to feet using our scale. So the first corridor measures 3 quarters of an inch. The second, measures one-half inch. The longest corridor is 1 and one-half inches long. And the final stretch is 1 and one-quarter inch. Using the Commutative Property, we can reorder these terms so that we can easily add our measurements together. Now we can see that Mike's 'x' is 4 inches from the cave's entrance. Just like before, we can use the scale ratio of three-quarters of an inch to five-eighths of a foot to find an equivalent ratio which has four inches as the numerator and the variable 'x' as our unknown denominator. Using cross-multiplication, we get 5 eighths times 4 equals 3 quarters 'x'. Then canceling on the left side of our equation, we multiply both sides by 4 thirds, to isolate 'x' and simplify. Haha, the perilous path is only 3 and a third feet long, in real life! This proves an interesting point about scales. Unlike with scale factors, it can be difficult to get a sense of comparison just from looking at the numbers in a scale. To review, scale factors always compare lengths using the same units, with a constant of proportionality, while scales are ratios that can use mixed units. When using a scale to compute an actual length, set up your scale ratio like a fraction, then use the information you know to set up a proportion. Then solve for the missing value. Frank braves the 3 and a third feet of darkness with his trusty rope, and hears the horrible sounds of... Yetis!! ...having a game night with Adventure Mike? And inside that mysterious package? Top secret, super-important batteries. Yeah, that was worth the trip.