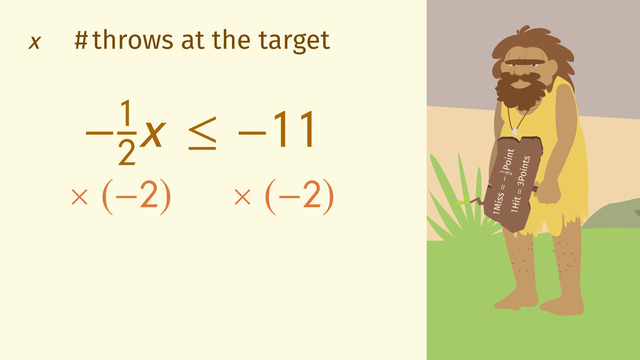Compound Inequalities

Basics on the topic Compound Inequalities
Compound inequalities are AND or OR inequalities. It’s important to understand the difference between AND and OR situations and also to recognize their graphs.
For an AND situation, a less than or less than and equal to situation such as -3 < x < 3, the solution is the intersection of the solution for x > -3 and x < 3. The graph of an AND situation (conjunction) will have one piece shaded. For an OR situation, such as x < -3 or x > 3, the solution is the union of the solution for each inequality.
The graph of an OR situation (disjunction) will be shaded in two pieces. How do you solve compound inequalities? Set up the inequalities as two separate inequalities then use algebraic steps to solve. To solve the inequalities, use opposite operations with reverse PEMDAS to isolate the variable.
Don’t forget about the sign. If multiplying or dividing by a negative number, remember to flip the sign so it points in the opposite direction. Otherwise, maintain the direction of the sign. Remember less than or less than and equal to situations are AND inequalities and greater than or greater than or equal to situations are OR inequalities. To investigate compound inequalities, watch this video.
Use inequalities to solve problems. CCSS.MATH.CONTENT.HSA.CED.A.3
Transcript Compound Inequalities
Jerry and Larry want to ride the rollercoaster, but they have a "little big" problem. What does this have to do with compound inequalities? Let me tell you.
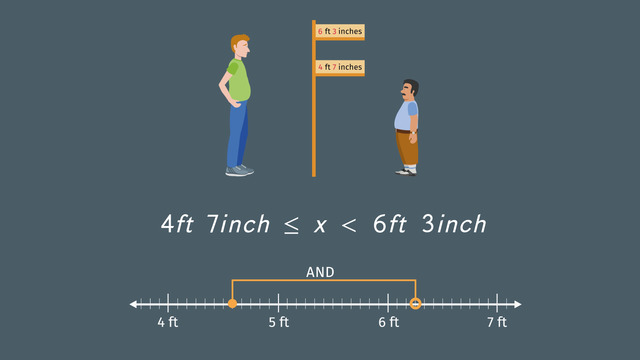
Let’s look at the problem first: You are only allowed to ride the rollercoaster if you are at least 4 feet 7 inches in height or shorter than 6 foot 3. Jerry is shorter than 4 foot 7 while Larry is taller than 6 foot 3.
Compound Inequalities on a Number Line: Conjunction and Disjunction
Let’s have a look at the number line to see how this problem can be represented graphically. It's not that you have to be an exact height to ride a rollercoaster, but you do have to be taller than a certain height as well as shorter than a certain height.
So you can say the height is greater than or equal to 4 foot 7, which is represented by a filled circle. Also, it has to be less than 6 foot 3, which is represented by an empty circle.
We'll use x to represent height. You can write this as a compound inequality with AND. x is less than 4 foot AND x is also less than 6 foot 3.
If you don’t look at the people who are allowed to ride the rollercoaster but instead at the people who aren’t allowed, like Jerry and Larry, you have a compound inequality with OR; either x is more than 4 foot 7 or x is greater than or equal to 6 foot 3.
This is represented graphically by these parts. Be careful: If you flip the wording in the problem, you also have to switch the circles! This means an empty circle at 4 foot 7 and an filled circle at 6 food 3.
How to solve Compound Inequalities: Conjunction
Let's take a look at an example to figure out how to calculate compound inequalities: 4 < 2x < 10.
This is a compound inequality with AND. So you can split this into two inequalities and put the word AND in between, ending up with one inequality, 4 < 2x and the other inequality is 2x < 10.
Now you calculate each inequality separately. Since we have 2x in both equations, we should divide both sides of both inequalities by two; the signs stay the same.
You can bring the two solutions, 2 < x and x < 5, back into one compound ineqality by reversing the process earlier. Remove the AND and now line up the Xs to get: 2 < x < 5.
How to solve Compound Inequalities: Disjunction
For compound inequalities with OR, you already have two seperate inequalities to begin with. So you simply calculate each individually.
In order to isolate the Xs, you have to eliminate 1 in the equation on the left, and 2 in the equation on the right. So you add 1 and 2 to the left and right equations, respectively.
Now you have to divide the equations by the coefficients, or the numbers in front of the x, which is 3 in the first equation and 4 in the second.
Your solutions, x < 5 and x > 12, can be brought together in the end with the word OR.
Let’s get back to Jerry and Larry. They really want to ride the rollercoaster. Jerry has an idea. Jerry decided to give his shoes to Larry. Now their heights are just right.
Compound Inequalities exercise
-
Write an inequality to describe the situation.
HintsThe phrases less than, at most, between, more than, or at least have special meanings in math.
For example, more than means $>$. The equal sign is not included.
At most $10$ means $\le 10$ and $10$ is included.
SolutionJerry and Larry want to ride the rollercoaster. They have a problem with the minimum and maximum height allowed to ride the roller coaster.
- At least $4$ feet $7$ inches can be expressed mathematically using $\ge$. So $x\ge 4$ feet $7$ inches or $4$ feet $7$ inches $\le x$.
- Shorter than $6$ feet $3$ inches can be expressed as $x<6$ feet $3$ inches.
-
Simplify the following inequalities.
HintsTo solve an inequality treat it like an equation and isolate the variable $x$ using opposite operations.
Remember, when multiplying with or dividing by a negative value, flip the sign!
Use Opposite Operations:
- Multiplication ($\times~\longleftrightarrow~\div$)
- Division ($\div~\longleftrightarrow~\times$)
- Addition ($+~\longleftrightarrow~-$)
- Subtraction ($-~\longleftrightarrow~+$)
SolutionLet's have a look at solving compound inequalities.
We start with a compound inequality: $4<2x<10$.
We can treat this inequality just like an equation by using opposite operations to isolate the variable $x$.
REMEMBER! If we multiply or divide both sides of the equation by a negative value, we have to flip the sign.
The left side divided by $2$ gives us $2<x$, and the right side becomes $x<5$. Because these inequalities are connected by the word and, we get the following compound inequality: $2<x<5$.
Next we look at $3x-1<14$ and $4x-2>46$.
First we transform the first inequality:
- Adding $1$ on both sides gives us $3x<15$
- Dividing by $3$ leaves us with $x<5$. Notice that the sign is still pointing in the same direction.
- Add $2$ to both sides to get $4x>48$
- Dividing by $4$ on both sides gives us our solution, $x>12$.
Let's have a look at the difference between and and or.
And means that both inequalities must be fulfilled. This can be seen as the intersection of two sets.
Or is a disjunction. This means that at least one of the inequalities has to be fulfilled.
-
Decide which number line belongs to which compound inequality.
HintsFirst, isolate the $x$.
- $<x$ less than, $x$ is not included
- $\le x$ at most, $x$ is included
- $>x$ greater than, $x$ is not included
- $\ge x$ at least, $x$ is included
SolutionWe can represent compound inequalities with number lines. We can indicate included numbers with filled circles and excluded numbers with empty circles.
First, we have to isolate the variable $x$ in each inequality.
$\begin{array}{rclcrccl} 3&<&3x&<&12&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 1&<&x&<&4 \end{array}$
This is the blue number line with two empty circles $4$ and $14$.
$\begin{array}{rclcrccl} 4&<&3x+1&\le&13&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 3&<&3x&\le&12&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 1&<&~~x&\le&4 \end{array}$
This is the green line number with an empty circle at $1$ and $4$.
$\begin{array}{rclcrccl} 3&\le&2x-5&\le& 9&&| (-~\leftrightarrow~+) \text{ Opposite Operations}\\ 8&\le&2x&\le&14&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 4&\le&~~x&\le &7 \end{array}$
This is the yellow line number.
$\begin{array}{rclcrccl} 5&<&3x-4&\le& 11&&| (-~\leftrightarrow~+) \text{ Opposite Operations}\\ 9&<&3x&\le&15&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 3&<&~~x&\le&5 \end{array}$
This is the red line number.
-
Solve the inequality.
HintsTo solve an inequality treat it like an equation, but don't forget to consider the sign.
Remember, if you multiply or divide by a negative value, you have to flip the sign!
Or more explicitly:
- $<$ changes to $<$, and vice versa
- $\le$ changes to $\ge$, and vice versa
SolutionWe can solve inequalities by following these simple steps:
- Use opposite operations
- If you multiply or divide by a negative number, flip the sign
- Isolate the variable $x$
This compound inequality can also be written as follows:
$1<x\le4$.
-
Explain what the inequality means.
HintsFor example, more than means $>$.
$\ge x$ means at least, $x$ is included
For example, less than means $<$.
$\le x$ means at most, $x$ is included
$2\le x\le4$ means that $x$ is $2$ or more as well as $4$ or less.
SolutionFirst let's have a look at the signs and their meanings:
- $<x$ less than, $x$ is not included
- $\le x$ at most, $x$ is included
- $>x$ greater than, $x$ is not included
- $\ge x$ at least, $x$ is included
-
Determine the opposite inequality.
HintsThe opposite of inclusion (and) is exclusion (or).
The opposite of
- $<$ is $\ge$
- $\le$ is $>$
SolutionThe opposite of inclusion (and) is exclusion (or).
If we want to examine all values for $x$ that don't satisfy the compound inequality $12\le3\times(x+2)<24$, we first have to isolate the variable $x$:
$\begin{array}{rcrcl} ~~\\ 12&\le& 3\times(x+2)&<&24&&|\text{ Distributive Property}\\ 12&\le& 3x+6&<&24\\ \color{#669900}{-6}&&\color{#669900}{-6}&&\color{#669900}{-6}&&| (+~\leftrightarrow~-) \text{ Opposite Operations}\\ 6&\le& 3x&<&18\\ \color{#669900}{\div3}&&\color{#669900}{\div3}&&\color{#669900}{\div3}&&| (\times~\leftrightarrow~\div) \text{ Opposite Operations}\\ 2&\le& x&<&6\\ ~~\\ \end{array}$
But what does this inequality mean? Right, both inequalities, $2\le x$ and $x<6$ have to be satisfied.
The opposite of the first inequality is $2>x$ or $x<2$. The opposite of the second inequality is given by $6\le x$.
The opposite of and is or. So the resulting compound inequality is
$x<2$ or $x\ge 6$.