Composite Area Problems

Basics on the topic Composite Area Problems
A complex composite area is determined by breaking up the composite shape into familiar shapes and then adding up the areas of the individual shapes. One application of composite areas is the tangram puzzle, where 7 polygonal shapes can be arranged in various ways to form different designs like boat, bird, dog, or house. Composite shapes abound in real life thus a knowledge in computing for the area is very useful. A city, for instance, is not usually shaped as a regular polygon so to get the area of a city, it must first be cut into sections, calculate the area for each, and then add up the areas of all sections. A knowledge of composite areas is also valuable when designing the perfect shape for a flight deck of an aircraft carrier to allow ease in simultaneous takeoff and landing. Learn how to get the area of a composite shape by helping rapper Notorious C.A.T. figure out the area of his cat-shaped pendant so he could cover it with diamonds for a perfect bling in his quest to take down and intimidate his rival rapper, MC Monta to become the best rapper on the block. Common Core Reference: CCSS.MATH.CONTENT.7.G.B.6
Transcript Composite Area Problems
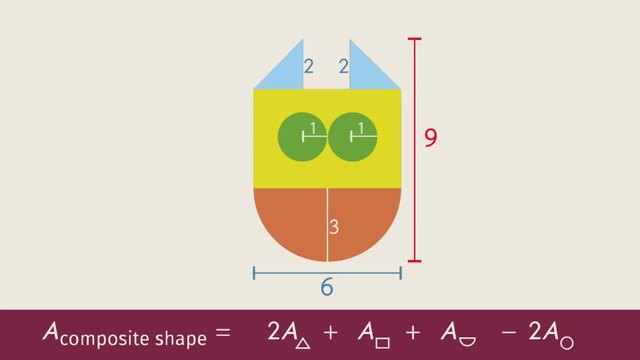
A rap battle is going on right here! Notorious C.A.T.'s rap game is on fleek. But, is he ready to take down his rival, MC Monta? We’re finally going to find out who’s the best rapper on the block. But, before they start spittin' rhymes Monta tries to intimidate C.A.T. with his bling. Monta brags that the chains he's wearing got more ice than Antarctica. Since bling's the thing C.A.T. wants to ice out his pendant like Monta. To figure out the area of his pendant that he needs to be covered in diamonds and shut down all the haters he’ll need to solve complex composite area problems. Let’s take a look at Notorious C.A.T.’s pendant. Whaaaat?! It’s in the shape of a cat?! I guess the cat's where it's at! To calculate the area, we’ll need to break down the composite shape into familiar geometric shapes. So, what do we know? Notorious C.A.T.'s pendant is composed of 2 isoceles right triangles 1 rectangle a semicircle and 2 emerald circles...you know...for the eyes. We don’t know all the measurements, but let's check out what we do know: We know that the total height of the pendant is 9 inches and the total width is 6 inches. The height of each isoceles right triangle ear is 2 inches and the radius of each circular eye is 1 inch. If these are the measurements we know, what dimensions do we need next? If the total width is 6 inches, how long is the radius of the semicircle? If you said 3 inches, you're exactly right! Also, notice that, since the total height of the pendant is 9 inches... We can subtract the known values from the total height of the pendant to find the height of the rectangle. And since the radius of the semicircle is 3 inches and the height of the triangle ears is 2 inches gives us 4 inches for the rectangle. Now, we’re ready to calculate the area of each shape. Do you remember how to find the area of a triangle? Yup! To find the area of any triangle, you multiply one half times the base times the height. Since Notorious's pendant has ears shaped like isoceles right triangles, we know that the length of the legs are each 2 inches long. Substituting the values for the triangle's base and height the area of EACH isoceles right triangle is 2 square inches... Now, on to the rectangular part of the face and we know that the area of a rectangle is width times height we can substitute 6 inches for the width and 4 inches for the height. Multiplying these together gives us the total area of the rectangular face. 24 square inches The cat pendant has emeralds for eyes already so we have to subtract the area of the eyes from the total area to know how much we need to cover using diamonds. But, how much area does each emerald eye take up? We already know that the area of a circle is pi times the squared radius Because the radius of each eye is 1 inch. The area of each emerald is equal to one pi square inches. The final part of the pendant is the semicircle. A semicircle is half of a circle so we can use the formula for area of a circle and simply multiply it by one half! We can see here that the radius is 3 inches. Therefore let's substitute the 3 inches. Simplified this results in nine pi over two square inches. We could also write this as 4.5π square inches. Finally, to calculate the area of the composite cat shape, we add and subtract the areas of the components we found. Substituting the known areas. Don't say just think. Area ears, area face, multiplying the ears and eyes by two combining like terms and then using the approximation 3.14 for π at the end to eliminate rounding errors results in the total area of the composite shape being approximately 35.85 square inches. Let's get back to reality and the battle of the bling. Monta don't care how much ice Notorious C.A.T. is rockin' because he's got the high quality gold and diamonds. It's delivery day and C.A.T. goes to check out his new pendant. MC Monta's jaw's gonna drop when he gets a load of this. Yo...for realz? His bling be made outta...chocolate!
Composite Area Problems exercise
-
Choose the geometric shapes that the pendant is composed of.
HintsLook at the cat ears and count the corners.
A shape with three corners is a triangle.
The pendant is composed of six shapes. Two of these shapes are the same.
SolutionTo determine the area of a composite shape, we first have to decide which shapes it is composed of.
In the case of Notorious C.A.T.'s pendant, we have:
- Two ears in the form of right triangles (the blue ones)
- One rectangular (the yellow one)
- One half circle (the red one)
- Two circles (the green ones), which we have to subtract from the sum of the areas of the other shapes, for the eyes of the pendant.
-
Calculate the area of the pendant.
HintsUse the lengths given in the description.
Keep in mind that the radius of a circle is half of the diameter:
- $r=\frac12 d$
- $d=2r$
Plug the given values into the corresponding formula for each shape.
SolutionWe already know the shapes that make up the pendant:
- two triangles (the ears)
- one rectangular
- one half circle
- two circles (the eyes)
Let's start with the ears, the triangles:
- $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
- Plugging in $2$ inches for both the base and the height gives us $A_{\text{triangle}}=\frac12(2)(2)=2~in^2$
We only know the width. The height has to be calculated by subtracting $2$, the height of the ears, and $3$, the radius of the half circle, from $9$. So we get $9-2-3=4$ inches for the height. Then we have:
- $A_{\text{rectangle}}=(\text{width})(\text{height})$
- Thus we have $A_{\text{rectangle}}=(6)(4)=24~in^2$
- $A_{\text{circle}}=\pi(\text{radius})^2$
- Plugging in the given radius, we get $A_{\text{circle}}=\pi(1)^2=\pi~in^2$
- $A_{\text{half circle}}=\frac12 \pi(\text{radius})^2$
- With the radius $3$ inches, we get $A_{\text{half circle}}=\frac12\pi(3^2)=4.5\pi~in^2$
$\begin{array}{rcl} A_{\text{composite area}}&=&2(2~in^2)+24~in^2+4.5\pi~in^2-2(\pi)~in^2\\ &=&28~in^2+2.5\pi~in^2\\ &\approx& 35.85~in^2 \end{array}$
-
Determine the area.
HintsYou can separate this shape into one rectangle and two triangles.
Both triangles have the same area.
The width of the rectangle is $4$ units and the height is $8$ units.
Use the following formulas:
- Rectangle: $A_{\text{rectangule}}=(\text{width})(\text{height})$
- Triangle: $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
SolutionThe shape above can be split up into a rectangle and two triangles with the same area. So we use the formulas,
- Rectangular: $A_{\text{rectangular}}=(\text{width})(\text{height})$
- Triangle: $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
- height: $8$ units, and
- width: $4$ units.
Next, we determine the base and the height of the triangle by counting the squares as well:
- base: $2$ units, and
- height: $2$ units.
Finally, we add both the area of the rectangle and twice the area of the triangle to get the total area of the shape: $A=32+(2)(2)=32+4=36$ units$^2$.
-
Calculate the area of the wooden heart.
HintsUse the formula for circle to get the area of the half circle by multiplying it by $\frac12$:
$A_{\text{half circle}}=\frac12\pi(\text{radius})^2$.
The radius is half the diameter.
Don't forget to add the results.
$\pi$ is approximately equal to $3.14$.
SolutionThis wooden heart is given by two half circles and one square.
The half circles have a radius of $\frac22=1$ inch. This is half of the diameter. We plug this in the formula to get,
$A_{\text{half circle}}=\frac12\pi(\text{radius})^2=\frac12\pi(1)^2=\frac12\pi\approx1.57$ $in^2$.
Next, we calculate the area of the square, which is given as the square of the side length:
$A_{\text{square}}=(\text{side})^2=(29)^2=4$ $in^2$.
Eventually, we are able to calculate the whole area:
$A=A_{\text{square}}+2~A_{\text{half circle}}=4+(2)(1.57)=4+3.14=7.14~in^2$.
-
Find the formula for the area of each given shape.
HintsThe area of a half circle is half of the area of a circle.
$\pi$ is used to determine the area or the circumference of a circle.
A right triangle is half of a rectangle.
SolutionTo calculate the areas we want, we need a few formulas:
- Rectangle: $A_{\text{rectangle}}=(\text{width})(\text{height})$
- Triangle: $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
- Circle: $A_{\text{circle}}=\pi(\text{radius})^2$
- Half circle: $A_{\text{half circle}}=\frac12\pi(\text{radius})^2$
-
Find the correct statements about the colored shape.
HintsUse the following formulas:
- Rectangle: $A_{\text{rectangular}}=(\text{width})(\text{height})$
- Triangle: $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
The width of the bigger rectangle is the height of the smaller one.
You need $b$ for each area.
SolutionThe colored shape is given by a triangle and a rectangle with another rectangle cut out of it. So we have to calculate the area of the bigger rectangle and the smaller rectangle, and then subtract the area of the smaller one from the area of the bigger one.
So, let's determine each area:
First, the area of the bigger rectangle:
- $A_{\text{rectangular}}=(\text{width})(\text{height})$,
- $A_1=(a)(b)$.
$A_2=(c)(b)$.
Lastly, we determine the area of the triangle:
- $A_{\text{triangle}}=\frac12(\text{base})(\text{height})$
- $A_3=\frac12(b)(d)$
$A=A_1-A_2+A_3$.
Let's take the results above to get
$A=(a)(b)-(a)(c)+\frac12(b)(d)$.
Each term has the same factor $b$. Thus, we can factor it out:
$A=b\left(a-c+\frac12d\right)$.