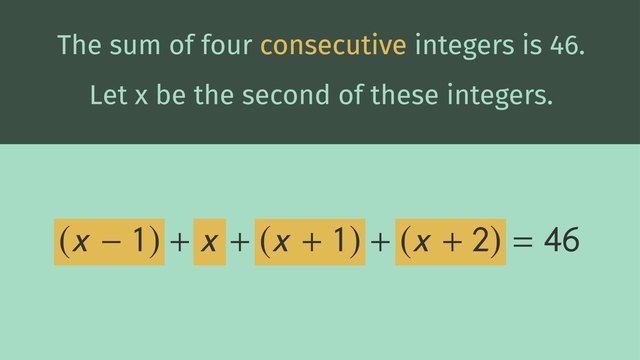Classifying Solutions of Linear Equations


Basics on the topic Classifying Solutions of Linear Equations
After this lesson, you will be able to identify how many solutions a linear equation has.
The lesson begins by teaching you that there are three types of solutions to linear equations. It leads you to learn that a linear equation sometimes has no, infinitely many, or exactly one solution. It concludes with examples of each of these three types of solutions.
Learn about classifying solutions of linear equations by helping Bert Cutler figure out the mystery behind their mystery game.
This video includes key concepts, notation, and vocabulary such as the phrase “false statement”, which is a short way of saying that a linear equation has no solutions.
Before watching this video, you should already be familiar with transforming or rewriting linear equations using the distributive property.
After watching this video, you will be prepared to learn how to find “consistent equations”, which are linear equations with exactly one solution.
Common Core Standard(s) in focus: 8.EE.C.7 A video intended for math students in the 8th grade Recommended for students who are 13 - 14 years old
Transcript Classifying Solutions of Linear Equations
Bert Cutler and the high school drama club are having a Murder Mystery party after school in the auditorium. Bert loves solving mysteries, so of course he is playing the detective. Everybody is acting a little suspicious. The butler looks shady, the groundskeeper is definitely hiding something, and the rich old lady is nervously clutching her pearls! So...who-dunnit? Bert goes with his gut and accuses the BUTLER! The players show their cards, but what’s this? Not only is the butler not guilty, but no one else is guilty, either. Somebody really messed up here. There’s no solution to the mystery! The drama club players reshuffle the cards and deal again. Bert accuses the groundskeeper and this time. He's right! The groundskeeper is guilty, but all the other players are guilty too! So, what 's going on? To figure out the mystery inside this mystery, we're going to have to investigate classifying solutions to linear equations. Just like the students' murder mystery game, a linear equation can have NO solution. Let’s look at an example. To calculate the solution to a linear equation, we need to follow the proper steps. First, to get rid of the parentheses, we’ll use the Distributive Property. Then, use opposite operations to isolate the 'x'. Hmm...this answer doesn't look right. 2 is NOT equal to 0. This is a false statement, which means there’s no solution to this linear equation. So, if after following the steps to solve a linear equation, you end up with an answer that looks like something like this, and 'a' and 'b' are not the same number. That means the linear equation has no solution. But there are also cases when a linear equation has an infinite number of solutions. Just like in the game when EVERYONE was guilty, in these cases ANY number can be a solution. Let’s take a look at an example. As always, follow the proper steps to solve the linear equation. First, use the Distributive Property to eliminate the parentheses and then combine the like terms. Look! Both sides of the equal sign are the same! We could simplify that even further by subtracting 2 from both sides, then 5x from both sides, and we end up with an equation that is obviously always going to be true. This means this linear equation has infinitely many solutions. So, if after following the proper steps, you get something that looks like this, or both sides of the equal sign have the same expression. It means there are infinite solutions to the linear equation. The last kind of solution is one that you've seen lots of times: a linear equation with just one solution. By now, you're a pro at this. Use the Distributive Property to write the equation without the parentheses. Combine the like terms and use opposite operations to isolate the variable. As you can see, there's just one solution to this linear equation. To review, there are three different kinds of solutions to linear equations. A linear equation can have no solution. You can recognize this when you end up with an equation like 2 equals 0, which is NOT (never) true. A linear equation can also have an infinite number of solutions. This is when you end up with an equation that is ALWAYS true, like zero equals zero. Finally, there can also be just one solution to a linear equation. These are equations like 5 equals 'x', where a variable is equal to a number. Bert's ready to solve the mystery. This time, he's sure he can identify the guilty person because there should be just one solution to this mystery. Bert takes center stage and accuses...himself! I knew there was something suspicious about that guy!
Classifying Solutions of Linear Equations exercise
-
Explain why the equations have one, infinitely many, or no solutions.
HintsEach linear equation leads to one of the following cases:
- a false equation, like $3=0$. In this case, the equation has no solution.
- an equation which is always true, like $3=3$, independent of the value of the variable. In this case, the equation has infinitely many solutions.
- an equation which is solvable, like $2x=4$. In this case, the equation has only one solution.
Here you see the distributive property.
Here you see an example for solving an equation using opposite operations.
SolutionTo solve a linear equation you isolate the variable by following the following steps:
- Use the distributive property to multiply parentheses.
- Combine the like terms.
- Use opposite operations to isolate the variable.
$\begin{array}{rclll} 2(3x+1) & = & ~6x&|&\text{ distributive property}\\ 6x+2&=&~6x\\ \color{#669900}{-6x} & &\color{#669900}{-6x}\\ 2&=&~0 \end{array}$
What's that? This isn't true at all. Thus the equation at the beginning can't be solvable; i.e. the equation has no solution.
Let's have a look at another example:
$\begin{array}{rclll} 3x+2(x+1)&=&~6x+2-x&|&\text{ distributive property}\\ 3x+2x+2&=&~6x+2-x&|&\text{ combine the like terms}\\ 5x+2&=&~5x+2\\ \color{#669900}{-2} & &\color{#669900}{-2}\\ 5x & = & ~5x\\ \color{#669900}{-5x} & & \color{#669900}{-5x}\\ 0 & = & ~0 \end{array}$
This equation is always true. So we can conclude that the starting equation has infinitely many solutions.
$\begin{array}{rclll} 4(5+x)&=&~5(2x+3)-5x&|&\text{ distributive property}\\ 20+4x&=&~10x+15-5x&|&\text{ combine the like terms}\\ 20+4x&=&~5x+15\\ \color{#669900}{-15} & &\color{#669900}{-15}\\ 5+4x & = & ~5x\\ \color{#669900}{-4x} & & \color{#669900}{-4x}\\ 5 & = & ~x \end{array}$
This is a clear solution. Such an equation has only one solution.
-
Describe how to determine if an equation has one, infinitely many, or no solutions.
HintsThis equation has no solution.
This equation has infinitely many solutions.
This equation has just one clear solution; it's $x=1$.
SolutionThere are only three possibilities for the solutions of a linear equation:
- No solution
- Infinitely many solutions
- One solution
No solution: If you end up with an equation like $a=b$ where $a$ and $b$ are not the same numbers, then you can conclude that the equation has no solution.
Infinitely many solutions: If you end up with an equation like $a=a$, then you can conclude that the equation has infinitely many solutions.
One solution: There exists only one clear solution, then you can conclude that the equation has on solution.
-
Find equations with one, infinitely many, or no solutions.
HintsIsolate the variable using opposite operations.
Each equation similar to $a=a$ indicates infinitely many solutions.
An equation $a=b$, where $a$ and $b$ are not the same number, indicates no solution.
SolutionIf you are able to solve an equation uniquely, like $3x=9$, then there is only one solution. In the case of $3x=9$, you have to divide both sides by $3$ to get $x=3$.
Another equation with only one solution is $2(x+1)=4x-(x+2)$:
- Using the distributive property leads to $2x+2=4x-x-2$.
- Next, we combine like terms: $2x+2=3x-2$.
- Subtracting $2x$ and $2$ results in $-4=x$.
Another equation with no solution is $2(x+1)=3x-(x+2)$:
- With the distributive property we get $2x+2=3x-x-2$.
- Next, we combine the like terms: $2x+2=2x-2$.
- Subtracting $2x$ leads to $2=-2$ a false equation.
Combing like terms in $3x+6x=9x$ leads to $9x=9x$ which is always true.
For $2(x-1)=3x-(x+2)$:
- Using the distributive property and combing like terms, we get $2x-2=2x-2$.
- Subtracting $2x$ and adding $2$ gives the equation $0=0$.
-
Determine which equations have one, infinitely many, or no solutions.
HintsSimplify each equation using the distributive property and combine like terms.
$x=0$ can be a true a solution to an equation.
There are three equations with one solution.
SolutionLet's start with the equations with one solution:
- $3x+2=2$: subtracting $2$ and dividing by $3$ after leads to $x=0$.
- $3x+2=2x+3$: subtracting $2x$ and $2$ leads to $x=1$.
- $4(x+2)=2(x+4)$ is equivalent to $4x+8=2x+8$. Now subtract $2x$ and $8$ to get $2x=0$. Dividing by $2$ leads to $x=0$.
- $3+2x=2x$: subtracting $2x$ leads to $3=0$, which isn't true at all.
- $4(x+2)=2(2x+4)-2$ is equivalent to $4x+8=4x+8-2$. Subtracting $4x$ and combining like terms leads to $8=6$, which is a false equation.
- $3x+2x=2x+3x$, which is equivalent to $5x=5x$. Subtract $5x$ to get $0=0$. This equation is always true.
- $4(x+2)=2(2x+4)$ is equivalent to $4x+8=4x+8$. This equation is always true.
-
Solve the equations which have one solution.
HintsUse the distributive property.
Here you see an example of combining like terms.
Here you see an example of using opposite operations.
SolutionTo solve linear equations you proceed as follows, perhaps in a different order:
- Use the distributive property.
- Combine like terms.
- Use opposite operations.
$~$
$\begin{array}{rclll} 3x+4&=&~13\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ 3x & = & ~9\\ \color{#669900}{\div 3} & & \color{#669900}{\div 3}\\ x & = & ~3 \end{array}$
$~$
$\begin{array}{rclll} 3(x+4)&=&~15&|&\text{ distributive property}\\ 3x+12&=&~15\\ \color{#669900}{-12} & &\color{#669900}{-12}\\ 3x & = & ~3\\ \color{#669900}{\div 3} & & \color{#669900}{\div 3}\\ x & = & ~1 \end{array}$
$~$
$\begin{array}{rclll} 3(x+4)-2x&=&~12&|&\text{ distributive property}\\ 3x+12-2x&=&~12&|&\text{ combine the like terms}\\ x+12&=&~12\\ \color{#669900}{-12} & &\color{#669900}{-12}\\ x & = & ~0 \end{array}$
$~$
$\begin{array}{rclll} 3(x+4)+2x&=&~4(x+1)&|&\text{ distributive property}\\ 3x+12+2x&=&~4x+4&|&\text{ combine the like terms}\\ 5x+12&=&~4x+4\\ \color{#669900}{-4x} & &\color{#669900}{-4x}\\ x+12 & = & ~4\\ \color{#669900}{-12} & & \color{#669900}{-12}\\ x & = & ~-8 \end{array}$
-
Identify which equation describes the story and how many solutions it has.
Hints$2$ times the sum of a number and $3$ is given by $2(x+3)$.
To isolate a variable, use the distributive property, pictured beside, and combine like terms.
SolutionFor the first story,
- Three times the sum of the unknown number and $2$ is given by $3(x+2)$.
- Three times the number added to $2$ can be written as $3x+2$.
$~$
For the second story,
- ... twice as old as the sum of his sister Anne's age and $2$ indicates $2(x+2)$.
- Together indicates addition: $x+2(x+2)=16$.
$\begin{array}{rclll} x+2(x+2)&=&~16&|&\text{ distributive property}\\ x+2x+4&=&~16&|&\text{ combine the like terms}\\ 3x+4&=&~16\\ \color{#669900}{-4} & &\color{#669900}{-4}\\ 3x & = & ~12\\ \color{#669900}{\div 3} & & \color{#669900}{\div 3}\\ x & = & ~4 \end{array}$
And so this equation has one solution.
$~$
For the last story,
We establish the equation step by step:
- The sum of the number and $4$: $x+4$.
- $7$ times this sum $7(x+4)$.
- Two times the sum of the number and two: $2(x+2)$
- Subtract ... $7(x+4)-2(x+2)$
- Triple of the number: $3x$.
- The double of the sum of the number and $12$: $2(x+12)$
- Added together we get $3x+2(x+12)$
Using the distributive property and combing like terms gives us
$7x+28-2x-4=3x+2x+24$, and thus $5x+24=5x+24$
an equation which is true for all $x$; this equation has infinitely many solutions.