Changing Scales


Basics on the topic Changing Scales
After this lesson, you will be able to create a scale drawing from an original drawing and identify the scale factor.
The lesson begins by reminding you that a scale factor, or constant of proportionality k, relates two proportional quantities using the equation y=kx. It leads you to learn how to create enlargements of a drawing using the equation Drawing=k(Original). It concludes with solving for the scale factor.
Learn about scale drawings by helping Carl enlarge his potato masterpiece!
This video includes key concepts, notation, and vocabulary such as enlargements (scale factors greater than 1) and the equation y=kx where k is the scale factor or constant of proportionality.
Before watching this video, you should already be familiar with finding the scale factor between two drawings, and multiplying and dividing fractions.
After watching this video, you will be prepared to learn…
Common Core Standard(s) in focus: 7.G.A.1 A video intended for math students in the 7th grade Recommended for students who are 12 - 13 years old
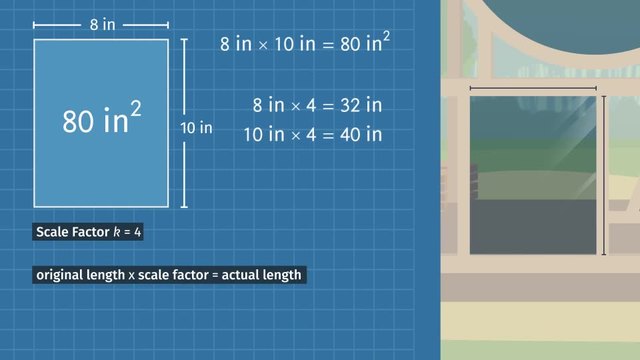
Transcript Changing Scales
Carl Toffel is an eccentric artist, known for his painstaking work on the subject of potatoes. Ah! After years of practice, Carl has created his stunning masterpiece, A Most Perfect Potato. To reproduce and display his artwork in many different sizes, Carl must know about changing scales. Carl wants to create a larger version of his masterpiece, A Most Perfect Potato. The original drawing is just too small to showcase the unparalleled glory of the potato! To do this, Carl will create an enlargement -- a scale drawing of his original work. Carl's original drawing is 3 feet by 3 feet, and Carl wants to enlarge it using a scale factor of 1.25. So, what will the dimensions of his new scale drawing be? Remember, the scale factor, or constant of proportionality, is the constant factor, 'k', relating two proportional quantities, 'y' and 'x'. So if the side lengths of the original and the scale drawing are proportional quantities with a scale factor of 1.25, then multiplying 3 by 1.25 will give us the sidelength of the enlargement: 3.75 feet! So, the enlarged scale drawing will measure 3.75 feet by 3.75 feet. But no! Carl decides even this drawing isn't big enough to show off the delicate, fine details of the exquisite potato. His final piece will be even larger, measuring an intimidating 15 feet by 15 feet! But what is the scale factor from Carl's medium drawing to his large drawing? Since the side lengths of the medium and the large drawings are proportional, we can set up the equation 15 equals 'k' times... 3.75, where 'k' is the scale factor. Then dividing both sides by 3.75, we find that 'k' equals 4. So, to get the large scale drawing, we must enlarge the medium drawing by a scale factor of 4. Now we've figured out the lengths and scale factors for all of Carl's drawings. Or have we?? Notice that the medium drawing is an enlargement of the original, and the large drawing is an enlargement of the medium drawing. Hmm, does that mean the large drawing is ALSO a scale drawing of the original? If that's true, we should be able to identify the scale factor from the original to the final drawing. Let's go step by step to find out. We know we can compare side lengths to figure out the scale factor. Carl's original drawing has side lengths of 3 feet, and the final drawing has side lengths of 15 feet. The scale factor between these two drawings would be the number 'k' which makes the equation 15 equals 'k' times 3 true. Therefore, dividing both sides by 3, we find that 'k' would have to equal 5. Indeed, scaling both sides of the original by 5 gives us the final drawing! So they are scale drawings of each other. That makes sense, because if two drawings are proportional to each other, a scale drawing of either one is a scale drawing of the other. Hmm, notice anything interesting about the number 5? Let's take a closer look. To get from the original, and smallest drawing, to the final, and largest drawing, on the diagram, we can hop from small to medium, and then from medium to large. Mathematically, we multiply the side lengths in the small drawing times a scale factor of 1.25 to get the side lengths of the medium drawing, and then multiply by a scale factor of 4 to get the side lengths of the largest and final drawing. So we can multiply these scale factors to get the scale factor from the small drawing to the large drawing. That's pretty neat! Let's review... To find the lengths in a scale drawing, or enlargement, take the lengths of the original drawing and multiply by the scale factor. Or, to determine the scale factor between two drawings, take a side length of the scale drawing and divide it by the corresponding side length of the original. If you make a scale drawing of a scale drawing, then both drawings are scale drawings of the original, just with different scales! To find the scale factor between any two drawings, you can multiply together the scale factors in a path that starts at the first drawing and ends at the second. At last, Carl unveils his 15 foot installation as part of the impressionist vegetable collection. It really is a most perfectly scaled potato.