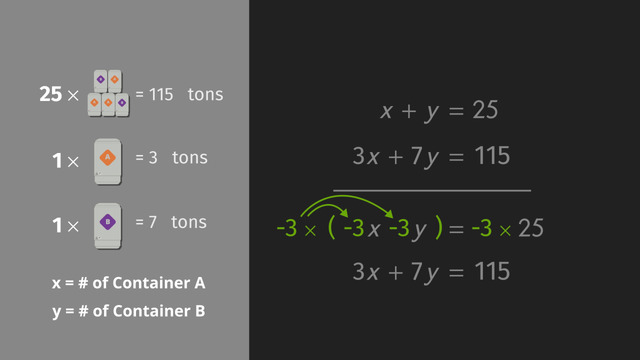Systems of Equations – Word Problems


Basics on the topic Systems of Equations – Word Problems
We often run into problems where we have multiple answers to find, and where the answers depend on each other. For instance, if we want to figure out what temperature it feels like outside, or the heat index, we would need to figure out both the air temperature and how humid it is outside.
Such problems, when expressed mathematically, end up givng a system of equations with multiple variables to solve for. Let’s look at a particular example: say your younger cousins worked part-time jobs over the summer to save money for a car. The job paid different rates for working weekdays and weekends. During the first week, one cousin worked 22 hours during the week and one hour on the weekend, earning $232. Her sister earned $270 by working 15 hours during the week and 10 hours on the weekend. What was the hourly pay rate for working weekdays and weekends?
When solving word problems, it is important to understand what you are asked to find. This problem is asking us to find the hourly pay rate for weekdays and the hourly pay rate for weekends. We will need to use different variables to represent each unknown. Let's use x for the weekday rate and y for the weekend rate. Now we can use the other information from the word problem to create equations that we will use to solve for the variables.
One cousin worked 22 weekday hours and one weekend hour for a total of $232. We can represent this with the equation 22x + y = 232. Using the pay for the other cousin, we get the equation 15x + 10y = 270. Since there are two equations with the same two variables, we can set them up as a system of equations and solve them simultaneously. 22x + y = 232 15x + 10y = 270
Here, we use substitution method to solve the system. The first equation can be solved for y by subtracting 22x from both sides of the equation. This leaves us with y=232 - 22x. Since y is equal to the expression 232 - 22x, we can substitute the expression for y in the second equation. The equation becomes 15x+ 10(232-22x) = 270. We now have one equation with one variable to solve.
15x + 10(232 - 22x) = 270 15x + 2320 - 220x = 270 2320 - 205x = 270 - 205x = -2 050 x = 10
We now know that the hourly pay rate for weekdays is $10. By substituting 10 for x in one of the equations, we can solve for y. Using the revised version of the first equation, we get y = 232 - 22(10) = 12.
Now that the values of both variables are known, the word problem is solved. The hourly pay rate is $10 for weekdays and $12 for weekends.
Solve Systems of Equations. CCSS.MATH.CONTENT.HSA.REI.C.5
Transcript Systems of Equations – Word Problems
Jessica is volunteering at the local animal shelter. Today, she has to buy some food and medication for the dogs and cats at the shelter. Jessica needs to figure out how much she can spend on supplies for the dogs and cats. This is an example of solving word problems using systems of equations.
Systems of Equations
There are 16 cats and 24 dogs in the shelter. Jessica has to buy supplies for the animals at the shelter. We'll let 'c' equal the cost of supplies for each cat and 'd' equal the cost of supplies for each dog, where Dog supplies cost twice as much as cat supplies. If Jessica has $640 to spend, how much can she spend on cat and dog supplies, respectively?
Let's see what we have. 16 cats times the cost of cat supplies, 'c', plus 24 dogs times the cost of dog supplies, 'd', equals the total cost, $640. So our first equation is 16c + 24d = 640. So, we have two variables in one equation. The second piece of information given is that dog supplies cost twice as much as cat supplies. The second equation we have to use is d = 2c.
Using Substitution to solve a System of Equations
We can use substitution to solve this system of equations. Since the second equation is already solved for the variable 'd', we can substitute 'd' with 2c in the first equation. The result is one equation with one variable, which we can solve now. Multiplying 24 and 2c, gives us 48c. We can add 16c and 48c on the left side of the equation, since these are like terms. This leaves us with 64c. The last step is to solve the equation by dividing both sides of the equation by 64.
We now know Jessica can spend $10 per cat. We still don't know how much to spend on dog supplies. But we do know how much Jessica can spend per cat. Let's plug in 10 for 'c' into the second equation. It doesn't matter if we use the first or second equation for this step, but the second is much easier, don't you agree?
Now we can solve this equation for 'd' by multiplying. We've determined that Jessica can spend $10 per cat and $20 per dog. Like a good math student, we should check our work. The solution to a system of equations must satisfy both equations. We have to substitute 10 for 'c' and 20 for 'd' in both equations. Let's start with the first equation. On the left side of the equation, the first step is to multiply, left to right, according to PEMDAS. The next step is to add, and we can see each side of the equation equals 640, letting us know that our solution is correct. Let's check the second equation to see if it's also correct. On the right side of the equation, we just have to multiply, and we can see that each side of the equation equals 20. The solution is also true for the second equation.
But Jessica still thinks the animal supplies costs a pretty penny. Looking for a better deal, Jessica finds a new shop offering discount dog supplies. She can buy all of the supplies she needs for 12 dogs at $210. She wonders, if she has to spend less on dog supplies, for how many additional cats will there be money for supplies?
Let's review the information we started with. We have an unknown number of cats, let this number equal 'x', with the cost of $10 for supplies for each cat. So we have 10x. We also have 24 dogs, and $640 to spend. This time we should use a new, second equation that reflects the store's special offer. Our second equation is 12 dogs times 'd', the cost of supplies for each dog, plus 0 cost for the number of cats times x, the number of cats, equals $210. We can use elimination to help solve this system of equations.
Notice what happens when the second equation is multiplied by -2, we get -24d = -420. Now we can eliminate the 24d in the first equation by adding the two equations together. Let's see what happens when we do that. We're left with 10x=220. Now all we have to do is divide both sides of the remaining equation by 10. Look at that!? Jessica can provide supplies for 22 cats with her budget. Since the shelter has 16 cats at the moment, she can provide supplies for 6 more cats.
Let's find out how much she spends with the special offer on the dog supplies. Either substitute 22 for 'x', or simply use the second equation since there is no 'x' anyway. The equation can be solved by dividing the number in front of 'd' in the equation. We know that Jessica spends $17.50 per dog at this store. Remember to check your work by substituting 22 for 'x' and 17.5 for 'd' into both equations. What a deal!
Solving a System of Equations graphically
In her pocket, Jessica finds $15 of her own. Jessica wants to buy some nice toys for her two favorite cats and her favorite dog with the money she saved. One doggy toy costs three times as much as one cat toy.
Let's do something a little different and solve this system of equations graphically. The first equation uses the information for 2 cats, 1 dog, and 15 dollars. The equation is 2x + y = 15. The second equation represents the fact that doggy toys are 3 times more expensive than cat toys. The equation is 3x = y. Each equation needs to be written in slope-intercept form to graph properly. For the first equation, subtracting 2x from both sides results in y = -2x + 15. The second equation is already in slope-intercept form.
Let's graph these lines on the coordinate plane. The solution to the system is the point of intersection for both lines. As we can see, the lines intersect at (3, 9) or x = 3 and y = 9. This means the cat toy is $3 and the dog toy is $9. Remember to do the check by substituting in 3 for 'x' and 9 for 'y' into both equations.
If only Jessica had known that the cats prefer the dog's toy . . .
Systems of Equations – Word Problems exercise
-
Determine the costs of supplies for cats as well as dogs.
HintsHere is an example for combining like terms:
$34a+17a=(34+17)a=51a$.
If one scoop of ice cream costs 1.5 dollars, then three scoops costs $3\times 1.5=4.5$ dollars.
So $x$ scoops of ice cream costs $1.5x$ dollars.
An example of solving equations using opposite operations:
SolutionJessica wants to know the cost of supplies for cats and for dogs, given that she only has $640$ dollars to spend.
First, we assign variables to the unknown values:
- $c$ for the amount of money she can spend per cat.
- $d$ for the amount of money she can spend per dog.
Taking into account the amount of money Jessica has at her disposal, we can see that the amount of money she can spend per cat $c$ and the amount of money she can spend per dog $d$ must satisfy the equation: $16c+24d$$=640$.
As supplies for a dog are twice as expensive as for a cat, we have that: $d=2c$.
Now we can substitute $2c$ for $d$ in the equation corresponding to the total cost to get: $16c+48c=640$. We can combine like terms to get: $64c=640$.
Lastly, we divide by $64$ to get $c=10$. Plugging this into the equation $d=2c$ gives us $d=20$.
-
Solve for the number of cats Jessica could buy supplies for.
HintsThe number of cats in which supplies can be purchased for multiplied by $10$ gives the amount of money left over after buying supplies for dogs.
To get the amount of money left over after purchasing dog supplies, subtract the cost of dog supplies from the amount of money Jessica has to spend; i.e. $640$ dollars.
SolutionWhat do we know?
- Jessica has $640$ dollars at her disposal.
- Supplies for one cat costs $10$ dollars.
- She has to buy supplies for $24$ dogs.
- The special offer is $210$ dollars for supplies for $12$ dogs.
So we can establish the following linear equations:
- $10x+24d=640$, for the total costs.
- $12d=210$.
Because we know that supplies for $12$ dogs cost $210$ dollars, we can conclude that the price for $24$ dogs is $420$ dollars.
Subtracting $420$ from $640$, we get that the amount of money left over for cat supplies is $640-420=220$ dollars.
We already know that the price of supplies for one cat is $10$ dollars. So lastly we divide $220$ by $10$ to get $220\div10=22$, the number of cats Jessica has money to buy supplies for after she buys supplies for 24 dogs for the special offer price.
-
Describe how to solve a system of equations by graphing.
HintsSlope-intercept form is given by $y=mx+b$, where $m$ is the slope and $b$ is the $y$-intercept.
Establish the equation describing the total cost.
Keep in mind that Jessica wants to buy two cat trees. This gives us $2y$.
The intersection of the lines corresponding to the equations in the system is the solution.
SolutionFirst, we assign variables to what is unknown:
- Let $x$ be the price of one dog basket.
- Let $y$ be the price of one cat tree.
Jessica has $48$ dollars in total. She wants to buy two cat trees and one dog basket. This gives us the equation $2y+x=48$.
One cat tree $y$ is one and a half times as expensive as one dog basket $x$. So we have $y=1.5x$; this equation is in slope-intercept form.
Transform the first equation to get it into slope-intercept form as well:
$\begin{array}{rcl} 2y+x&=&48\\ \color{#669900}{-x} & &\color{#669900}{-x}\\ 2y & = & -x+48\\ \color{#669900}{\div2} & & \color{#669900}{\div2}\\ y & = & -\frac12 x+24 \end{array}$
You can see the corresponding lines above. The intersection is given by $x=12$ and $y=18$.
Let's check algebraically that this is indeed the solution:
- $2\times 18+12=36+12=48$ $~~~~~$✓
- $1.5\times 12=18$ $~~~~~$✓
-
Determine the price of dog as well as cat supplies.
HintsRemember to use substitution.
By eliminating one variable, you get one equation in one variable; use opposite operations to solve this equation.
Check your solution: both equations must be satisfied.
SolutionLet's start with the first equation:
We substitute $1.5x$ for $y$ in the equation $12x+8y=240$ to get $12x+8(1.5x)=240$. Combining like terms leads to $24x=240$. Lastly, we divide by $24$ to get $x=10$. Again using $y=1.5x$ we can conclude that $y=15$. Let's check that the solution works:
- $12\times 10+8\times 15=120+120=240$ $~~~~~$✓
- $1.5\times 10= 15$ $~~~~~$✓
Substitute $2.5x$ for $y$ in the equation $12x+8y=128$ to get $12x+8(2.5y)=128$. Combining like terms gives us $32x=128$. Dividing by $32$ results in $x=4$. Multiplying by $2.5$ leads to $y=10$. Once again we check the solution:
- $12\times 4+8\times 10=48+80=128$ $~~~~~$✓
- $2.5\times 4= 10$ $~~~~~$✓
- $5\times 24+5\times 12=120+60=180$ $~~~~~$✓
- $2\times 12= 24$ $~~~~~$✓
-
Explain how to solve systems of equations.
HintsHere is an example of a system of equations:
- $2x+3y=7$
- $x=2y$
In the system of equations given in the first hint, $x$ equals $2y$. So plug in $2y$ for $x$ in the first equation to get $2(2y)+3y=7$.
Keep in mind that you have to find solutions which satisfy all equations.
SolutionA system of equations is not only one equation with one variable, but two equations with two variables, or more equations with more variables!
Remember that solutions to a system of equations must satisfy every equation in the system. Not just one equation in the system.
How can we solve a system of equations?
We can eliminate one variable; let's have a look at the following example:
- $2x+3y=7$
- $x=2y$
We can also get the solution by graphing: we draw the lines corresponding to the equations in a coordinate system. The point of intersection gives us the solution, as pictured above!
-
Decide which graph belongs to the system of equations.
HintsYou can check the intersection of the lines each time. The intersection point must satisfy both equations.
You can write an equation like $2x+y=3$ in slope-intercept form by subtracting $2x$ from both sides: $y=-2x+3$.
First, draw the $y$-intercept and then the slope; remember, it's rise over run!
Lines corresponding to $y=mx$ pass through the origin.
SolutionTo draw the lines corresponding to a system of equations, we first write each equation in a slope-intercept form: $y=mx+b$:
$\begin{array}{rcl} x+y&=&6\\ y&=&2x \end{array}$
The second equation is already given in slope-intercept form. Dividing both sides by $x$ in this equation leads to $y=-x+6$. So we have to look for two lines, one with a $y$-intercept of zero and the other with a $y$-intercept of $6$. The solution is given by $x=2$ and $y=4$.
Now we look at the next system of equations:
$\begin{array}{rcl} x-y&=&0\\ -x+3y&=&6 \end{array}$
The first equation is equivalent to $y=x$ and the second to $y=\frac13x+2$. The $y$-intercepts are zero and $2$. The solution is given by $x=3$ and $y=3$.
The next one:
$\begin{array}{rcl} 2x+3y&=&12\\ 5x+3y&=&21 \end{array}$
The first equation can be written in slope-intercept form: $y=-\frac23x+4$. The second as well can be written in slope-intercept form: $y=-\frac53x+7$. The $y$-intercepts are $4$ and $7$ and the solution is $x=3$ and $y=2$.
And for the last example:
$\begin{array}{rcl} 2x+y&=&6\\ -x+y&=&3 \end{array}$
Rewriting both equations in slope-intercept form gives us $y=-2x+6$ and $y=x+3$, with $y$-intercepts $6$ and $3$. The solution is given by $x=1$ and $y=4$.