Inequalities
Easy learning with videos, exercises, tasks, and worksheets
Most popular videos
Content
- Introduction
- Graphing Inequalities
- One-Step Inequalities
- Two-Step Inequalities
- Multi-Step Inequalities
- Compound Inequalities
Introduction
Inequalities are similar to equations, but their solution sets include values that are less than, less than or equal to, greater than and greater than or equal to.
These inequalities model the four different inequality symbols:
- $x<10$
- $x\leq10$
- $x>10$
- $x\geq10$
Graphing Inequalities
To graph the solution set of an inequality, pay close attention to the symbol used in the problem. An open circle indicates less than or greater than, whereas a closed circle indicates less than or equal to or greater than or equal to.

One-Step Inequalities
To solve one-step inequalities, follow the same procedures as when solving one-step equations with one exception. When multiplying or dividing by a negative number, remember to flip the inequality symbol.
To solve this one-step inequality, you can use mental math.
$\begin{array}{lcr} -2x&\lt &14 \\ \frac{-2}{-2}x&\lt& \frac{14}{-2} \\ ~~~~~x&\gt& -7x \end{array}$
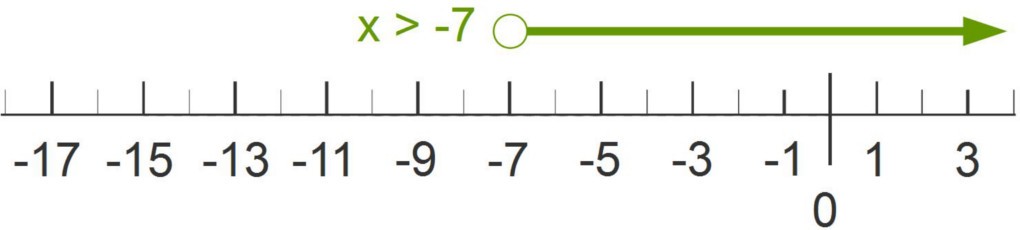
Use the opposite operation to undo the constant found in this inequality.
$\begin{array}{lcr} x -5&\leq&15 \\ x -5 +5&\leq&15 +5 \\ x&\leq&20 \end{array}$

When solving one-step inequalities, watch out for graphing errors. The graph of this problem has an open circle.
$\begin{array}{lcr} x +3 &\gt& 5 \\ x+ 3 -3&\gt&5 -3 \\ x&\gt&2 \end{array}$

The graph of this one-step inequality has a closed circle.
$\begin{array}{lcr} ~2x&\geq&10 \\ \frac{2}{2}x&\geq&\frac{10}{2} \\ ~~~x&\geq&5 \end{array}$
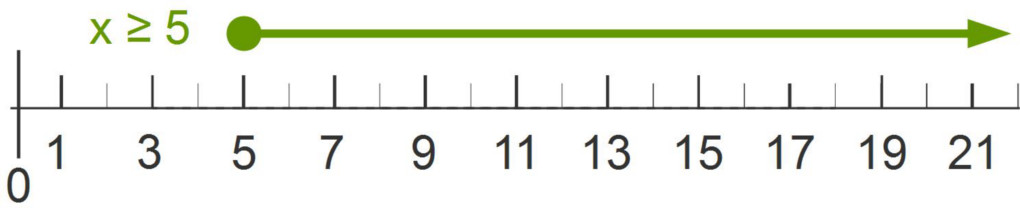
Two-Step Inequalities
Just like one-step inequalities, two-step inequalities follow the same procedures as equations, but watch out for multiplying or dividing by negative numbers.
To solve this problem, use two steps, but watch out for the negative coefficient.
$\begin{array}{lcr} ~~~7&\gt&-2x -1 \\ ~~~7 +1&\gt&-2x -1 +1 \\ ~~~8&\gt&-2x \\ ~\frac{8}{-2}&\gt&\frac{-2}{-2}x \\ -4&\lt& x \end{array}$

To solve this two-step inequality, use the multiplicative inverse to undo the coefficient.
$\begin{array}{lcr} \frac{x}{2} -8&\geq& -9 \\ \frac{x}{2} -8 +8&\geq& -9 +8 \\ \frac{x}{2}&\geq& -1 \\ \frac{x}{2}\times2&\geq& -1\times2 \\ x&\geq& -2 \end{array}$

Multi-Step Inequalities
Similar to multi-step equations, multi-step inequalities can have numbers and variables on either side of the inequality sign. Combine like terms first, and remember to watch out for sign changes due to multiplying or dividing by a negative number.
The graph of this multi-step inequality has a pen dot.
$\begin{array}{lcr} ~8x +4 -2x&\lt&12 \\ ~6x +4&\lt&12 \\ ~6x +4 -4&\lt&12 -4 \\ ~6x&\lt&8 \\ \frac{6}{6}x&\lt&\frac{8}{6}\\ ~~~x&\lt&\frac{8}{6} \\ ~~~x&\lt&1\frac{1}{3} \end{array}$
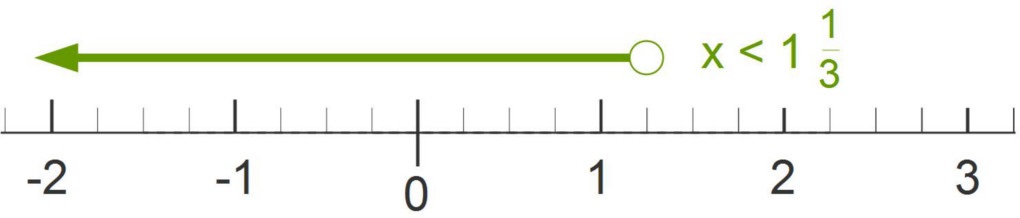
When solving inequalities with negative numbers, it’s smart to check if the inequality changes direction.
$\begin{array}{lcr} -18&\leq& -5x + -x \\ -18&\leq& -6x \\ ~\frac{-18}{-6}&\leq&\frac{-6}{-6}x \\ ~~~3&\geq& x \end{array}$

Compound Inequalities
Compound inequalities are also known as and and or compound inequalities because they contain inequalities that are separated by the words and and or.
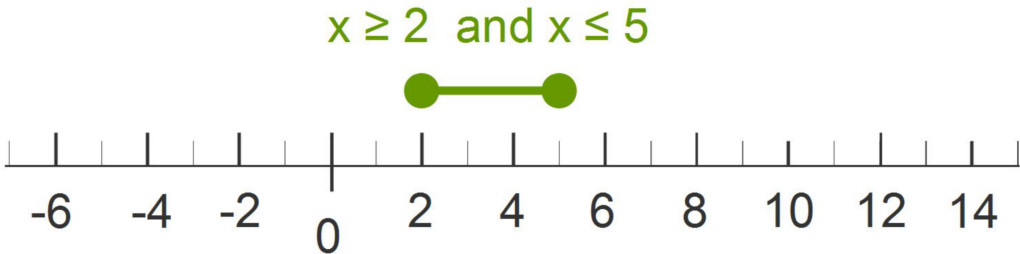
This inequality can be written as two inequalities separated by the word and.
$\begin{array}{lcccr} 2~\leq~~~&x&~~~\leq~5 \\ x~\geq~2& \text{and}&x~\leq~5 \end{array}$
Graphs of AND inequalities show only one piece of the graph shaded. The and represents an intersection.
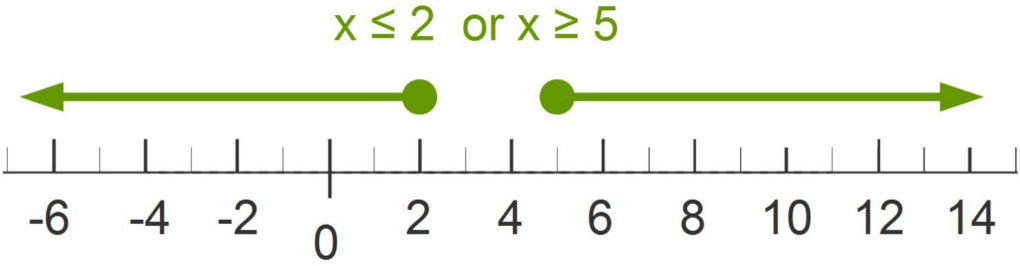
$x\leq2 \quad \text{or} \quad x\geq5$
Graphs of OR inequalities show two separate pieces of the graph shaded. The or represents a union.
All videos on the topic
Videos on the topic
Inequalities (6 videos)
All worksheets on the topic
Worksheets on the topic
Inequalities (6 worksheets)









 Inequalities and Their Graphs
Inequalities and Their Graphs
 Solving One-Step Inequalities by Adding or Subtracting
Solving One-Step Inequalities by Adding or Subtracting
 Solving One-Step Inequalities by Multiplying or Dividing
Solving One-Step Inequalities by Multiplying or Dividing
 Solving Two-Step Inequalities
Solving Two-Step Inequalities
 Solving Multi-Step Inequalities
Solving Multi-Step Inequalities
 Compound Inequalities
Compound Inequalities









