Equations

Content

• Solving Equations
  • One-Step Equation
  • Two-Step Equation
  • Multi-Step Equation with Variable on One Side
  • Multi-Step Equation with Variables on Both Sides
• Word Problems
• Distance Rate Time
  • Distance Rate Time – Same Direction
  • Distance Rate Time – Different Directions

Solving Equations

Equations containing one or more variables are algebra equations. Variables represent unknown amounts, and any letter or symbol can be used as a variable.

Algebra equations may need one-step, two-steps, or multiple-steps to solve for the value of the variable. Equations may have variables on one or both sides of the equal sign. To solve algebra equations, students combine like terms and use inverse operations to isolate the variable. Equations in the format of variable word problems may help students learn to apply algebra skills to real world situations.

One-Step Equation

To isolate the variable to solve these one-step equations, undo the equation:

Example 1: Undo the constant by subtracting from both sides of the equation.

$\begin{array}{lcl} x + 3 & = & 8 \\ x + 3 - 3 & = & 8 - 3 \\ x & = & 5 \end{array}$

Example 2: Divide both sides of the equation by the coefficient.

$\begin{array}{lcl} 2x & = & 16\\ \frac{2}{2}x & = & \frac{16}{2} \\ x& = &8 \end{array}$

Two-Step Equation

Use reverse PEMDAS to solve this two-step equation.

Step 1: Subtract the constant from both sides of the equation.
Step 2: Divide both sides of the equation by the coefficient.

$\begin{array}{lcl} 3x + 5 &= & 17 \\ 3x + 5 -5 &= &17 -5\\ 3x&=&12 \\ \frac{3}{3}x&=&\frac{12}{3} \\ x&=&4 \end{array}$

Multi-Step Equation with Variable on One Side

Use the Distributive Property to solve this multi-step equation:

Step 1: Apply the Distributive Property.
Step 2: Add the constant to both sides of the equation.
Step 3: Divide both sides of the equation by the coefficient.

$\begin{array}{lcl} 8 &= &2(x - 2)\\ 8&=&2x -4 \\ 8 +4&=&2x -4 +4 \\ 12&=&2x \\ \frac{12}{2}&=&\frac{2}{2}x \\ x&=&6 \end{array}$

Multi-Step Equation with Variables on Both Sides

To solve multi-step equations such as this, combine like terms to make the problem easier to solve:

Step 1: Use opposite operations to combine like terms.
Step 2: Divide both sides of the equation by the coefficient.

$\begin{array}{lcl} 11x&=& -16 + 3x\\ 11x - 3x &=& -16 + 3x- 3x \\ 8x &=& -16 \\ \frac{8}{8}x&=&\frac{-16}{8}\\ x&=& -2 \end{array}$

Word Problems

Write a variable equation to solve this word problem. Let x represent the number of people attending the party.

Husni bakes cakes for a party. He doesn’t know how many people will attend, but he does know he needs 3 eggs per cake and a cake serves 8 people. Write an expression to determine the number of eggs he will need.

$(\frac{x}{8})\times3$

If 24 people attend the party, how many eggs will he need?

$(\frac{24}{8})\times3 = 3\times3=9$

He needs 9 eggs.

Distance Rate Time

Use the Distance Rate Time (DRT) formula to solve problems of how far, how long, or how fast. Using the formula, calculate problems for travel in the same direction or different directions. The following triangles will help you to remember:

Distance Rate Time – Same Direction

Example 1: Use the DRT formula to solve this problem: Alex rode his bike for 2 hours travelling 23 miles. What is his rate?

D = 23 miles
T = 2 hours
R = x

$\begin{array}{lcl} 23&=&2x\\ x&=&11.5 \end{array}$

Alex’s rate is 11.5 miles per hour.

Example 2: After school, Kara and Cyrus ride bikes with the riding club. Kara leaves school at 3:00 pm, riding 10 miles per hour. Cyrus stayed a few minutes late to clean out his locker and left at 3:10 pm, riding at a rate of 12 miles per hour. When will he catch up with Kara?

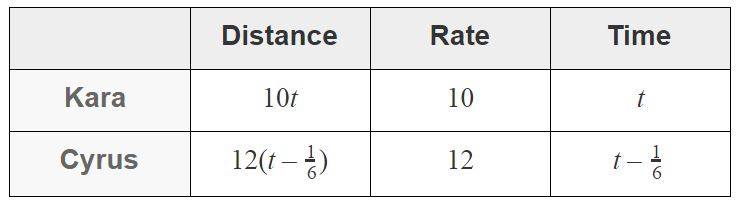
$\begin{array}{lcl} 10t &=& 12(t-\frac{1}{6}) \\ 10t&=&12t -2 \\ 10t -12t&=&12t -12t -2 \\ -2t&=&-2 \\ \frac{-2}{-2}t&=&\frac{-2}{-2} \\ 2t&=&2 \\ t&=&1 \end{array}$

After one hour, Cyrus will catch up with Kara.

Distance Rate Time – Different Directions

For this problem, the travel is from two different directions. Use the DRT formula to solve: Carly and Pete leave school traveling in opposite directions on a straight road. Pete rides his electric bike 12 mi/h faster than Carly walks. After 2 hours, they are 36 miles apart. Find Carly’s rate and Pete’s rate.

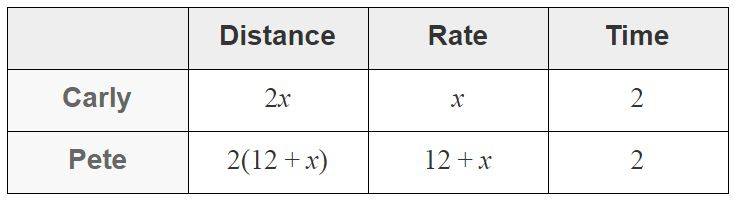
$\begin{array}{lcl} 2(12+x) + 2x &=&36\\ 24 +2x +2x&=&36\\ 24 +4x&=&36\\ 24 -24 +4x&=&36 -24\\ 4x&=&12\\ \frac{4}{4}x&=&\frac{12}{4} \\ x&=&3 \end{array}$

Carly’s rate is 3 mph, and Pete’s rate is 15.