Using Triangles to Find the Area of Trapezoids
- Finding the Area of Parallelograms and Trapezoids
- Finding the Area of a Trapezoid
- Decomposing a Trapezoid
- Using the Formula to Find the Area of a Trapezoid

Basics on the topic Using Triangles to Find the Area of Trapezoids
Finding the Area of Parallelograms and Trapezoids
Imagine you're an artist planning to paint a canvas that's shaped like a door (parallelogram) or a kite (trapezoid). Before you start, you need to know how much paint you'll need. That's where calculating the area of a shape, or the space inside these shapes, becomes very important. Today, we're going to learn exactly how to do that, making sure we have enough paint and don't run out!
Parallelogram: A shape where opposite sides are parallel and equal in length, like a slanted rectangle.
Trapezoid: A shape with at least one pair of parallel sides. Think of it as a stretched-out triangle with a flat top.
Finding the Area of a Trapezoid
The area is the amount of space inside a shape. For parallelograms and trapezoids, there are a variety of different methods that can be used to find the area.
| Method | Description | When to Use |
|---|---|---|
| Decomposing into Two Triangles | This method involves dividing the trapezoid into two triangles by drawing a line from one vertex to the opposite vertex. Then, calculate the area of each triangle and add them to find the total area. | Useful when the height and the lengths of the parallel sides (bases) are known. It simplifies the calculation by breaking the shape into simpler parts. |
| Using a Formula | The formula for the area of a trapezoid is $\frac{base_1 + base_2}{2} \times height$. This method is straightforward and quick, requiring only the lengths of the bases and the height. | Best for situations where quick calculations are needed, and all the necessary measurements are readily available. |
A simple way to visualize this is to see how to find the area of parallelograms and trapezoids on the coordinate plane.
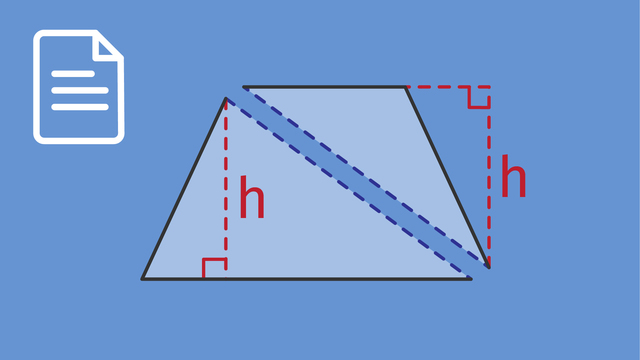
Decomposing a Trapezoid
Imagine cutting a trapezoid into two smaller triangles to make it easier to measure. We can measure the area of each triangle and then add them together to find the total area of the trapezoid. This is called decomposing a shape.
Decomposition of a shape refers to the process of breaking down a complex geometric figure into simpler parts, such as triangles, rectangles, or other polygons, that are easier to analyze or measure. This technique is often used in mathematics to simplify the calculation of areas, volumes, and other properties of shapes.
Find the area by decomposing it into two triangles and finding the sum of their area.
The trapezoid has two base measurements, $6$ cm and $10$ cm, and the height is $4$ cm. Decompose the figure into two triangles.
Now each triangle uses one of the bases of $6$ cm and $10$ cm. Use the formula for the area of a triangle ($A=\frac{1}{2}bh$) to find the area of each triangle separately, and then find the sum of their areas.
| Calculation for Triangle A | Calculation for Triangle B |
|---|---|
| Base: $b = 6$ cm | Base: $b = 10$ cm |
| Height: $h = 4$ cm | Height: $h = 4$ cm |
| Area: $A = \frac{1}{2} \times b \times h$ | Area: $A = \frac{1}{2} \times b \times h$ |
| $A = \frac{1}{2} \times 6 \times 4 = 12$ cm$^2$ | $A = \frac{1}{2} \times 10 \times 4 = 20$ cm$^2$ |
Next, find the sum of the two triangles.
$12$ cm$^2 + 20$ cm$^2 = 32$ cm$^2$
The total area of the trapezoid is $\bf{32}$ cm$\bf{^2}$.
Using the Formula to Find the Area of a Trapezoid
Finding the area of a trapezoid can be done quickly using a formula. This method is efficient and requires just a few measurements: the lengths of the two parallel sides (bases) and the distance between them (height).
Area of a Trapezoid Formula
$base_1$ and $base_2$: These are the lengths of the two parallel sides of the trapezoid. It doesn't matter which one you call $base_1$ or $base_2$; just make sure you use both.
Height: This is the perpendicular distance between the two bases. It's important not to confuse this with the slant height or the length of the non-parallel sides.
Find the area of a trapezoid with $base_1 = 8$ cm, $base_2 = 5$ cm, and a height of 4 cm.
- Identify the bases and the height: $base_1 = 8$ cm, $base_2 = 5$ cm, and the height $= 4$ cm.
- Substitute into the formula: Area $= \frac{(8 + 5)}{2} \times 4 $
- Solve: Area $= \frac{13}{2} \times 4 = 26$ cm$^2 $
The area of the trapezoid is 26 cm².
Finding the Area of a Trapezoid – Summary
Key Learnings from this Text:
- Understanding the area of parallelograms and trapezoids is crucial for various mathematical and real-life applications.
- Like all problems, finding the area of a trapezoid can be done with a variety of different methods, including decomposition, and using a formula.
- Decomposing shapes and using formulas are effective methods to find areas.
- Knowing how to calculate these areas helps in planning, designing, and executing projects that involve these shapes.
Finding the Area of a Trapezoid – Frequently Asked Questions
Transcript Using Triangles to Find the Area of Trapezoids
The mayor of Polygon, Pennsylvania is launching a "Revitalize the City" campaign to engage people in projects that make their city a better place to live. Today, she's meeting with a citizen who wants to bring some color and flair to some of the city's many dumpsters! It's an opportunity to turn a trash heap into a cultural epicenter. All it will take is a little paint, hard work, and, well two methods for using triangles to find the area of trapezoids. The sides of all of the city's dumpsters are shaped like trapezoids. A trapezoid is a quadrilateral where at least two of the four sides are parallel. This dumpster has parallel sides of 8 feet and 12 feet. It also has a height of 5 feet. In order to determine how much paint will be needed to give this dumpster a makeover, we're going to need to find the area. Let's try a strategy you may have used before. Imagine decomposing this trapezoid into smaller shapes which will help us find the area. Hmm, this isn't very helpful. Neither is this. But what if we cut along the diagonal? Now to get the trapezoid's total area, we can just add the area of these triangles together. We'll call the bottom triangle, triangle 1 and the top triangle, triangle 2. What information do we have about triangle 1? Well we know that this side has a length of 12 feet. Let's call that our base. We also know that the perpendicular distance from the base to the top of the triangle is 5 feet. That's our height. Remember the base and height of a triangle are always perpendicular to each other. That is indicated by this right angle sign, here. Now how can we use that information to find the area of triangle 1? Remember that the area of any triangle can be found by multiplying one-half the base, 'b', times the height, 'h'. Substituting these values into our formula triangle 1 has an area of 30 square feet. Now let's look at triangle 2. The area of this triangle is also going to be one-half the base times the height. So what's the base? Well we only know one side length, so let's use that for our base. Now what should we use for our height? Notice that because the bases we used are parallel, the heights of both triangles are the same. Multiplying one half our base and height gives us an area of 20 square feet for triangle 2. Adding the area of our two triangles together gives us a total area for the trapezoid of 50 square feet. Now to give this dumpster a splash of color! For our next example, here's another design by our local citizen. This one is painted on a rectangular canvas, and she wants to use glue to attach it to a dumpster. So we're going to need to use triangles again to figure out the area of a trapezoid. This canvas is composed of three shapes: the trapezoid in the middle and two triangles on the sides which we'll call triangle 1 and triangle 2. Our plan is to first find the area of the enclosing rectangle then subtract the areas of the two triangles leaving us with the area of the trapezoid. We can express this process with the formula: total area equals area of the rectangle, minus the sum of triangle 1 and triangle 2. Let's start by finding the area of the rectangle. Multiplying 12 feet times 5 feet gives us an area of 60 square feet. Let's plug that value into our formula before we move on. Now to figure out the area of triangle 1. What values should we use for the base and height? The base and height are perpendicular to each other so the area of this triangle will be one-half 3 feet times 5 feet. That gives us 7.5 square feet which we can substitute into our equation. Now, we can turn our attention to the final piece of the puzzle: triangle 2. Triangle 2 has a base of 1 foot and height of 5 feet. That makes its area 2.5 square feet. Substituting that into our equation. Then simplifying we get the area of the trapezoid, 50 square feet. Now, while the dupster artist puts the finishing touches on her work let's review our methods. We looked at two strategies using triangles to find the area of trapezoids. For the first strategy, we can decompose a trapezoid into triangles by drawing a diagonal from opposite corners. Then, using the area formula one-half base times height we find the area of both triangles and add them together. For our second strategy we compose a rectangle around the trapezoid, creating two new triangles. Then, we find the total area of the enclosing rectangle and subtract the areas of the two new triangles. Which method you use depends on the information you are given and of course, which approach you prefer. It's time for the grand dumpster unveiling! Wow, what a difference a little paint can make. Now the citizens of Polygon are lined up for hours just to throw away their trash.
Using Triangles to Find the Area of Trapezoids exercise
-
Find the area of a trapezoid by decomposing the figure.
HintsOne strategy to find the area of a trapezoid is to decompose the shape into two triangles. You can then find the area of each triangle and add the values together.
Decomposing a shape means dividing it into smaller, simpler parts, such as triangles or rectangles.
To find the area of a triangle, use the formula: $A=\frac{1}{2}bh$.
SolutionStep 1: Decompose the trapezoid into 2 triangles.
Step 2: Use the area of a triangle formula: $A=\frac{1}{2}bh$ and substitute in the base and height of each triangle.
- $A=\frac{1}{2}(5)(2)$
- $A=\frac{1}{2}(3)(2)$
- $A=3$ m$^2$
- $A=5$ m$^2$
$A = 3 + 5$
Step 5: Find the total area of the trapezoid.
$A = 8$ m$^2$
-
Decompose the trapezoid into two triangles to find the area.
HintsThe height of a triangle is always perpendicular to the base of the triangle.
To find the area of this triangle, we can identify the base and height first.
base = $24\:m$
height = $10\:m$
Next, substitute the values into the formula: $A=\frac{1}{2}bh$.
$A=\frac{1}{2}(24)(10)$
Solve for the area.
$A=120\:m^2$
SolutionTriangle 1:
$A_1=\frac{1}{2}bh$
$A_1=\frac{1}{2}(6)(5)$
$A_1=15$ in$^2$
Triangle 2:
$A_2=\frac{1}{2}bh$
$A_2=\frac{1}{2}(10)(5)$
$A_2=25$ in$^2$
The area of both triangles can be added together to find the total area of the trapezoid!
-
Find the area of a trapezoid using triangles.
HintsOne strategy used to find the area of a trapezoid is seen here in this image and formula.
To use this method, you must know the formulas:
Area of a Rectangle $A=lw$
Area of a Triangle $A=\frac{1}{2}bh$
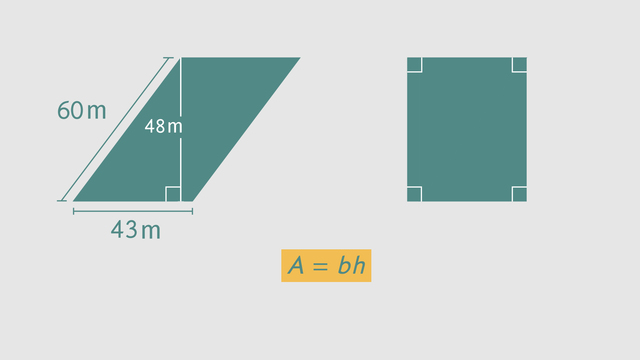
To better understand this method, imagine you have a rectangle on paper and you know the area. You can then use scissors to cut off the two corner triangles to be left with only the trapezoid.
SolutionOne of the strategies for finding the area of a trapezoid is to first find the area of the enclosing rectangle, and then subtract the areas of the two triangles.
The formula we can use for this calculation is Area = $\bf{A_\square - (A_{\Delta 1}+A_{\Delta 2})}$.
The area of the enclosing rectangle can be found with the formula $A=lw = (10)(4)$. The rectangle has a total area of $\bf{40\:cm^2}$. The formula to find the area of a triangle is $\bf{A=\frac{1}{2}bh}$. Triangle 1 has an area of $4\:cm^2$ and triangle 2 has an area of $2\:cm^2$. The total triangle area is $\bf{6\:cm^2}$.
Use the formula, $A_\square - (A_{\Delta 1}+A_{\Delta 2})\:$ , and substitute the known values, ($40 - 6$) to find the area of the trapezoid.
Area = $\bf{34\:cm^2}$.
-
Find the area of the trapezoid by using triangles.
HintsRemember to use triangles to help you find the area of the trapezoid. The best strategy for this question:
- Decompose the trapezoid into two triangles and find the sum of their areas.
The formula Area = $A_{\Delta1}+A_{\Delta2}$ can be used when decomposing the trapezoid.
SolutionThe area of the trapezoid is $\bf{150\:ft^2}$
Triangle 1:
$A=\frac{1}{2}(12)(10) = 60$
Triangle 2:
$A=\frac{1}{2}(18)(10) = 90$
$60+90=150$
-
What do you know about trapezoids?
HintsBe sure to use the image to help you determine which statements are true about trapezoids.
Parallel sides on a trapezoid will look like this.
There are 4 correct statements.
SolutionThese four statements are true about trapezoids:
- Trapezoids can be decomposed into 2 triangles.
- Trapezoids have 4 sides.
- Trapezoids are quadrilaterals.
- Trapezoids have at least 2 of 4 sides parallel to each other.
-
Use triangles to help you find the area of a trapezoid.
HintsOne strategy learned to find the area of a trapezoid is decomposing the shape into two triangles. The area can be found of each triangle separately and then combined for the area of the trapezoid.
Another strategy learned to find the area of a trapezoid is to first find the area of the enclosing rectangle. Then find the area of the two triangles created on the side and subtract the areas of these from the rectangle.
SolutionThere are two strategies to find the area.
Strategy 1 Decompose the trapezoid into two triangles, find the area of each, and then find the sum of the areas.
$\begin{array}{l}A=\frac{1}{2}bh\\ A_{\Delta 1\ }=\frac{1}{2}\left(14\right)\left(6\right)\\ A_{\Delta 1\ }=\ 42\\ A_{\Delta 2}\ =\ \frac{1}{2}\left(8\right)\left(6\right)\\ A_{\Delta 2}=\ 24\\ A=42+24\\ A=66\ cm^2\end{array}$
Strategy 2 Find the area of the enclosed rectangle, and subtract the two triangles created on the sides from the rectangle.
$\begin{array}{l}A=lw\\ A=\left(14\right)\left(6\right)\\ A=\ 84\ cm^{2\ }\\ \\ A=\frac{1}{2}bh\\ A_{\Delta 1}=\frac{1}{2}\left(3\right)\left(6\right)\\ A_{\Delta 1}=\ 9\\ A_{\Delta 2}=\frac{1}{2}\left(3\right)\left(6\right)\\ A_{\Delta 2}=\ 9\\ \\ A=84-\left(9+9\right)\\ A=66cm^2\\ \end{array}$






















can I post this to my googleclassroom? Is there a way to share with students to watch individually?